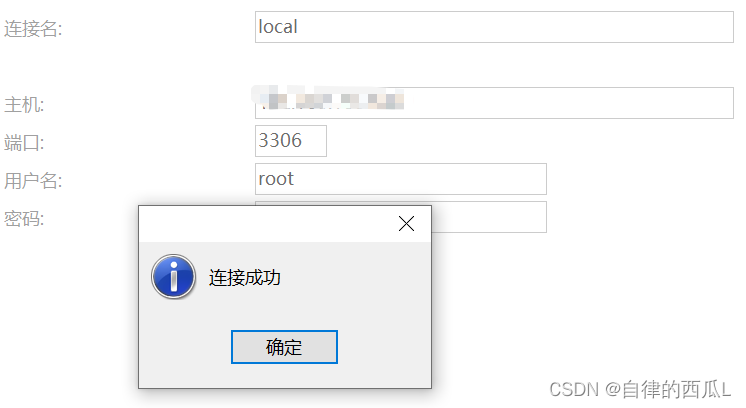
先说寻找旋转排序数组中的最小值 I

题目：
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

题解：
这个比较简单，比如 4 5 6 1 2 3
那么我们二分查找，即可找到
二分的判断条件为 是否小于 nums[0] 的值
l 设为 0，r 设为 nums.size() - 1，是一个左开右闭区间（不包括第一个值）
如果 nums[mid] 小于 nums[0]，则 r = mid（包括 mid）
如果 nums[mid] 大于 nums[0]，则 l = mid（不包括 mid）

注意还要加上，如果 1 2 3 4 5，则我们找的范围不包括第一个值，所以会错过 1
所以最后的结果，需要和 nums[0] 比较，取最小值

代码如下

class Solution {
public:int findMin(vector<int>& nums) {int l = 0, r = nums.size() - 1, mid;while(l < r - 1) {mid = (l + r) / 2;if(nums[mid] > nums[0]) {l = mid;}else if(nums[mid] < nums[0]) {r = mid;}}return min(nums[0], nums[r]);}
};

再说寻找旋转排序数组中的最小值 II

题目：
已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须尽可能减少整个过程的操作步骤。

题解：
第一次看到这种考虑的不是最坏情况的算法题，想错解法了

这种题，肯定不能用二分
如果 4 4 4 0 4 4 4 4 4 4 4 4，我怎么找到这个最小值
二分的话，需要可以判断来缩小下一次寻找范围
这个 nums[mid] 为 4 的话，得不到任何消息
所以如果考虑这种特殊情况的话，那肯定复杂度为 O(n)，需要遍历一次

但是题目的意思是，尽可能的优化，那应该怎么考虑呢
尽可能的用二分，并对特殊情况进行特判
比如之前题目中

if(nums[mid] > nums[0]) {l = mid;
}
else if(nums[mid] < nums[0]) {r = mid;
}

需要对等于的情况进行特判，比如 4 x x x x 4 x x x x 4
我们肯定是要缩小范围的，但是呢，又只能一个一个减小范围（不然可能会漏掉）
怎么一个一个缩小呢，可以比较如果两边边界，如果等于 nums[mid]，则可以向左或者向右移动一个，缩小边界

代码如下

class Solution {
public:int findMin(vector<int>& nums) {int l = 0, r = nums.size() - 1, mid;while(l < r - 1) {mid = (l + r) / 2;if(nums[mid] > nums[0]) {l = mid;}else if(nums[mid] < nums[0]) {r = mid;}else {if(nums[r] == nums[0]) {r--;}if(nums[l+1] == nums[0]) {l++;}}}return min(nums[0], nums[r]);}
};