一 点睛
构造最小生成树还有一种算法,即 Kruskal 算法:设图 G=(V,E)是无向连通带权图,V={1,2,...n};设最小生成树 T=(V,TE),该树的初始状态只有 n 个节点而无边的非连通图T=(V,{}),Kruskal 算法将这n 个节点看成 n 个孤立的连通分支。它首先将所有边都按权值从小到大排序,然后值要在 T 中选的边数不到 n-1,就做这样贪心选择:在边集 E 中选择权值最小的边(i,j),如果将边(i,j)加入集合 TE 中不产生回路,则将边(i,j)加入边集 TE 中,即用边(i,j)将这两个分支合并成一个连通分支;否则继续选择下一条最短边。把边(i,j)从集合 E 中删去,继续上面的贪心选择,直到 T 中的所有节点都在同一个连通分支上为止。此时,选取的 n-1 条边恰好构成图 G 的一棵最小生成树 T。
Kruskal 算法用一种非常聪明的方法,就是运用集合避圈;如果所选择加入边的起点和终点都在 T 集合中,就可以断定会形成回路,变的两个节点不能属于同一个集合。
二 算法步骤
1 初始化。将所有边都按权值从小到大排序,将每个节点集合号都初始化为自身编号。
2 按排序后的顺序选择权值最小的边(u,v)。
3 如果节点 u 和 v 属于两个不同的连通分支,则将边(u,v)加入边集 TE 中,并将两个连通分支合并。
4 如果选取的边数小于 n-1,则转向步骤2,否则算法结束。
三 图解
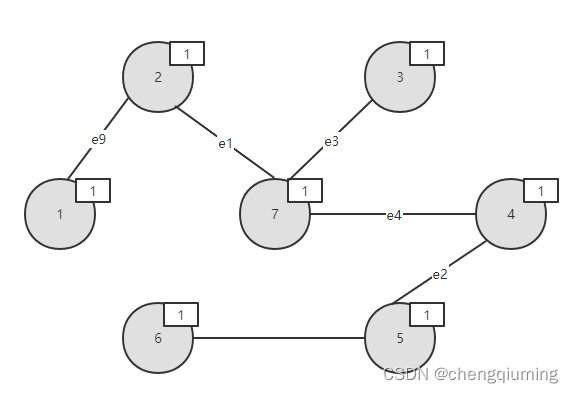
设图 G=(V,E)是无向连通带权图。
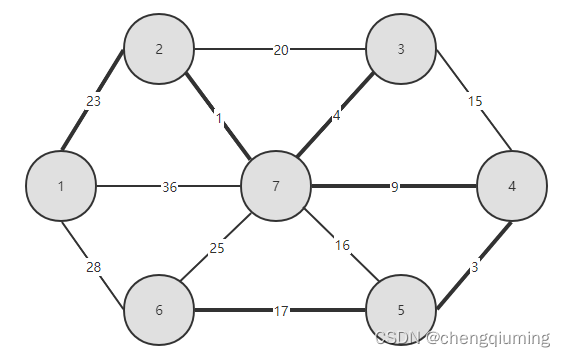
1 初始化
将所有边都按权值从小到大排序,如下图所示。将每个节点都初始化为一个孤立的分支,即一个节点对应一个集合,集合号为该节点的序号,如下图所示。

2 找最小
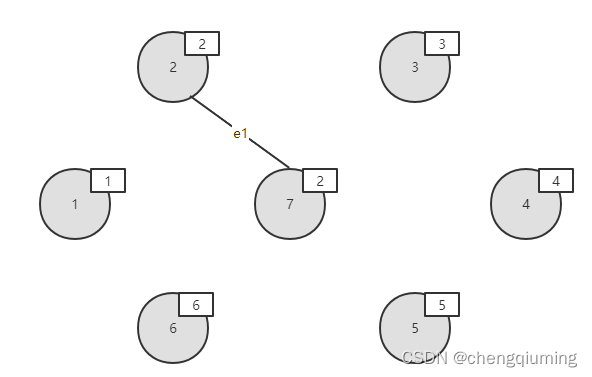
在 E 中寻找权值最小的边e1(2,7),边值为1.
3 合并
节点2 和节点7的集合号不同,即属于两个不同的连通分支,将边(2,7)加入边集 TE 中,执行合并操作,将两个连通分支的所有节点都合并为一个集合;假设把小的集合号赋值给大的集合号,那么节点7的集合号将改为2.如下图所示。
4 找最小
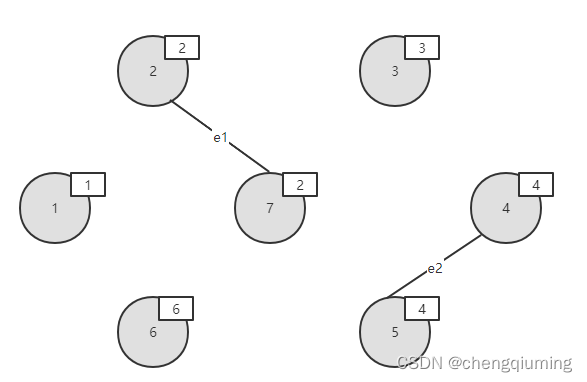
在 E 中寻找权值最小的边e2(4,5),边值为3.
5 合并
节点4 和节点5的集合号不同,即属于两个不同的连通分支,将边(4,5)加入边集 TE 中,执行合并操作,将两个连通分支的所有节点都合并为一个集合;将节点 5 的集合号将改为4.如下图所示。
6 找最小
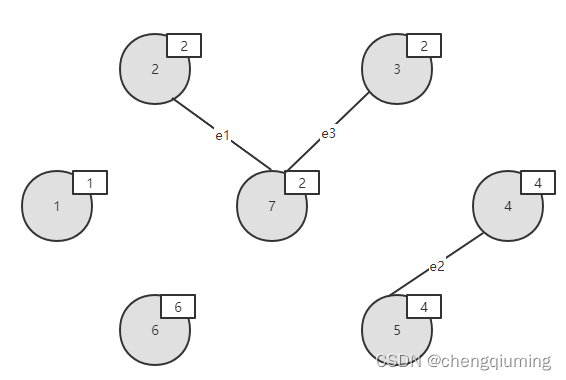
在 E 中寻找权值最小的边e3(3,7),边值为4.
7 合并
节点3 和节点7的集合号不同,即属于两个不同的连通分支,将边(3,7)加入边集 TE 中,执行合并操作,将两个连通分支的所有节点都合并为一个集合;将节点 3 的集合号将改为2.如下图所示。
8 找最小
在 E 中寻找权值最小的边e4(4,7),边值为9.
9 合并
节点4 和节点7的集合号不同,即属于两个不同的连通分支,将边(4,7)加入边集 TE 中,执行合并操作,将两个连通分支的所有节点都合并为一个集合;将节点 4、5 的集合号将改为2.如下图所示。
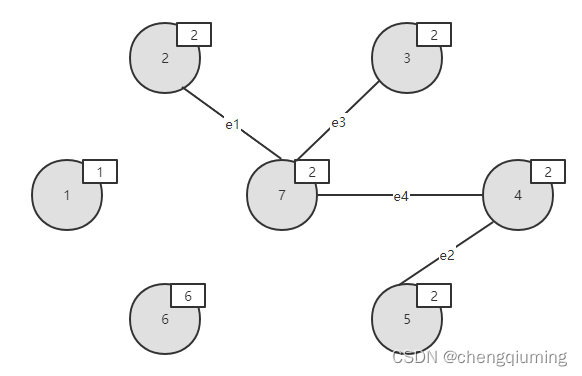
10 找最小
在 E 中寻找权值最小的边e5(3,4),边值为15.
11 合并
节点3 和节点4的集合号相同,属于相同的连通分支,不能选择,否则会形成回路。
12 找最小
在 E 中寻找权值最小的边e6(5,7),边值为16.
13 合并
节点5 和节点7的集合号相同,属于相同的连通分支,不能选择,否则会形成回路。
14 找最小
在 E 中寻找权值最小的边e7(5,6),边值为17.
15 合并
节点 5 和节点 6 的集合号不同,即属于两个不同的连通分支,将边(5,6)加入边集 TE 中,执行合并操作,将两个连通分支的所有节点都合并为一个集合;将节点 6 的集合号将改为2.如下图所示。
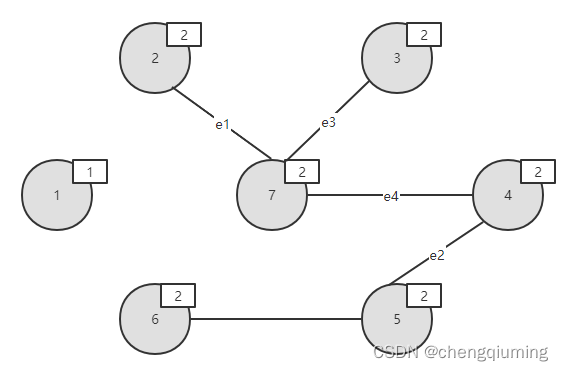
16 找最小
在 E 中寻找权值最小的边e8(2,3),边值为20.
17 合并
节点2 和节点3的集合号相同,属于相同的连通分支,不能选择,否则会形成回路。
18 找最小
在 E 中寻找权值最小的边e9(1,2),边值为23.
19 合并
节点 1 和节点 2 的集合号不同,即属于两个不同的连通分支,将边(1,2)加入边集 TE 中,执行合并操作,将两个连通分支的所有节点都合并为一个集合;将节点 2,3,4,5,6,7 的集合号将改为1.如下图所示。