第六章 管理类联考基础逻辑——综合推理*****
一、数学相关
数学题包含比例,集合,不等式,概率等。重视思维考察,计算量小。(考1-2题)
考点1:集合
画饼集能力1

A∪B=A+B-A∩B
A∩B=A+B-A∪B2
考点2:比例
考点3:不等式
1)举反例:
常用反例反向:①最平均分配:33,33,34;3
②最不平均分配:1,1,98。
2)针对人数的联言、选言:
对于“且”,上下限取小值;对于“或”,上下限取大值。
考点4:概率
二、综合推理
综合推理主要是排列组合和配对题,方法就是画表+排除法。此类题是近年热点,可达到6-7题,其中难题2-3题。难题往往比较耗时,能否在复杂条件中找到突破口有一定运气成分。此类题风险大,建议放在考试最后做。(题号53,54,55中最少有两道超难综合推理题)
考点1:排序(简单题:条件不需要综合运用)
解题方法:画表+排除456
秒杀:选项给出所有匹配,选多法。
考点2:配对题
常规法:配对78
秒杀:条件没提及的对象,选项选没有提及的对象。9
两种情况下的排除(难)10
以上第二章到第七章是推理题,推理题可公式化,不需读懂题,以下第八章到第十章是论证题,找论证结构,需读懂题,需记住套路。
论证题(10-15题):必考五类题:削弱、假设(最难,考必要条件)、支持(考最多,超论证题的一半)、解释、结论。

画饼题-两个饼-最简单的画饼题
1.参加某国际学术研讨会的 60 名学者中,亚裔学者 31 人,博士 33 人,非亚裔学者无博士学位的 4 人。根据上述陈述,参加此次国际研讨会的亚裔博士有几人?
A.1 人。
B.2 人。
C.4 人。
D.7 人。
E.8 人。
【解析】选 E。
亚裔学者 31 人,博士 33 人,非亚裔学者无博士学位的 4 人,这三者加起来是 68 人,但实际总人数有 60 人,亚裔学者和博士两个概念之间为交叉关系,这两 个概念和非亚裔学者无博士学位者之间都是全异关系。这说明,既是亚裔学者又
是博士即亚裔博士有 8 人。
方法二:
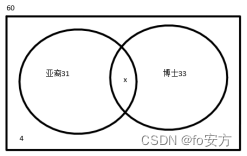
31+33-x=60-4,得:x=8 ↩︎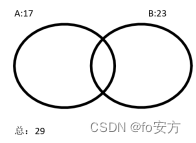
17+23-29=11 ↩︎不等式问题-超难题
杉杉外国语大学规定:“只有成绩优良并且每学期参加社会工作满10小时以上,才能获得优秀毕业生资格”,同时规定“只要成绩优良并且每学期都参加社会工作满10小时以上,就能够得到政府工作推荐”(其他不满足条件的,也可能得到工作推荐,上限为总人数或者无穷个),(得逻辑模型:优→成良且10→工作)根据统计,杉杉外国语大学西班牙语专业2011级毕业生一共有29名,其中成绩优良的一共17人,每学期参加社会工作满10小时以上的一共23人。(得:成良且10取值范围:17+23-29=11至17)根据以上统计数据,关于杉杉外国语大学西班牙语专业2011级毕业生的以下断定哪项一定为真。(求:优先且工作)
A.一共有11名毕业生既获得优秀毕业生资格又得到政府工作推荐
B.一共至少有11名毕业生既获得优秀毕业生资格又得到政府工作推荐
C.一共至多有11名毕业生既获得优秀毕业生资格又得到政府工作推荐
D.一共至少有17名毕业生既获得优秀毕业生资格又得到政府工作推荐
E.一共至多有17名毕业生既获得优秀毕业生资格又得到政府工作推荐
超难题:需要先看例1-3理解概念,才能代入对应概念做题。
例1:中国人且美国人→中国人。中国人为(14亿-15亿),那么中国人且美国人可为0个人-15亿。(有助理解,不是小范围推大范围)
例2:中国人(10亿-14亿)→生物。生物最小下限为中国人的最小值10亿,最大值为无穷。
例3:(有助理解)
先去掉概率,换成字母进行理解。
A→B→C,已知人数11≤B≤17人数,求A且C范围?(是人数,不是数字)
可得:A的范围为:A不能超过B的范围,最小可为0人,最大为17人。0≤A≤17。
可得:C的范围为:有B就有C,B在C内部,所以C最小为11,最大为总人数29。11≤C≤29。(看题干,具备条件可推出C,不具备也可能推出C)
最后,对于且,上下限取小值,0≤A且C≤17。(拓展:A或C,上下限取大值,11≤A或C≤29)
方法一:秒杀:选项有“且”,下限几乎都为0,可排除“至少”超过0:B,D。C选项≤11;E选项≤17。C可推E,得:C真则E真。排除C选项,选E。
方法二:共100人:A=9,B=7,A且B的范围:0≤A且B≤7。
A=17,B=23,A且B的范围:0≤A且B≤17。
拓展:A=17,B=23,A或B的范围:23≤A或B≤40。(或:一真则真,B→A或B) ↩︎排序题
甲、乙、丙、丁四人的国籍分别为英国、俄国、法国、日本。乙比甲高,丙更矮;英国人比俄国人高,法国人最高;日本人比丁高。
这四个人的国籍是:
A.甲是英国人,乙是法国人,丙是俄国人,丁是日本人。
B.甲是法国人,乙是日本人,丙是俄国人,丁是英国人。
C.甲是日本人,乙是法国人,丙是英国人,丁是俄国人。
D.甲是俄国人,乙是法国人,丙是日本人,丁是英国人。
E.甲是日本人,乙是法国人,丙是俄国人,丁是英国人。
秒杀:选项给出所有匹配,选多法。“乙是法国人”,排除B。“丙是俄国人”排除C,D。“丁是英国人”排除A,C。选E。
常规法:画表+排除。
高 → 矮
一 二 三 四
丙
法
第一步:法为非丙;非甲;非丁。所以法为乙。
高 → 矮
一 二 三 四
乙 丙
法
由“日本人比丁高”结合上图,得:
高 → 矮
一 二 三 四
乙 丁 丙
法 日
由“英国人比俄国人高”,得:
高 → 矮
一 二 三 四
乙 丁 丙
法 日 英 俄 ↩︎真题2016-画表排除法-最高难度
54-55题基于以下题干
江海大学的校园美食节开幕了,某女生宿舍有 5 人积极报名参加此次活动,她们
的姓名分别为金粲、木心、水仙、火珊、土润。举办方要求,每位报名者只做一
道菜品参加评比,但需自备食材。限于条件,该宿舍所备食材仅有 5 种:金针菇、
木耳、水蜜桃、火腿和土豆。要求每种食材只能有 2 人选用。每人又只能选用 2
种食材, 并且每人所选食材名称的第一个字与自己的姓氏均不相同。 已知:
(1)如果金粲选水蜜桃, 则水仙不选金针菇;(由(2)得,水选金,所以否后为真,则否前也为真,金不选水。结合图,得:土选水。)
(2)如果木心选金针菇或土豆,则她也须选木耳;(突破口:否后为正确,非选木→非选金和木,结合图,得:木选水火。影响(4))
(3)如果火珊选水蜜桃,则她也须选木耳和土豆;(假设火选水,则选了三个,错误,∴火不选水,结合图,得:火选木和土)
(4)如果木心选火腿,则火珊不选金针菇。
54.根据上述信息, 可以得出以下哪项? (由(2)得:肯前则肯后,火不选金为真,结合图,得:水选金,土选金)
A.木心选用水蜜桃、土豆。
B.水仙选用金针菇、火腿。
C.土润选用金针菇、水蜜桃。
D.火珊选用木耳、水蜜桃。
E.金粲选用木耳、土豆。
54.【解析】选 C。
由条件(2)可知:木心不选金针菇、土豆、木耳,木心只能选火腿、水蜜桃;
由条件(4)可知,火珊不选金针菇,再由(3)可知,火珊不选水蜜桃,由题干
可知:火珊不能选火腿,综合推出:火珊只能选木耳、土豆;由题干可知:金粲
不能选金针菇,由前述又可知:木心、火珊都没选金针菇,所以只能是水仙、土
润选金针菇;因为水仙选金针菇,由条件(1)可知,金粲不能选水蜜桃,由前
述可知,火珊也不选水蜜桃,再由题干可知,水仙不能选水蜜桃,所以只能是木
心、土润选水蜜桃;由此可得结论:土润选金针菇、水蜜桃,所以 C 正确。
方法二:画表排除
人 金 木 水 火 土
菜 ---------------------
金 × × √ × √
木 × √ ×
水 × √ × × √
火 √ × ×
土 × √ ×
可得:土选金和水,选C。
55.如果水仙选用土豆, 则可以得出以下哪项?
A.木心选用金针菇、水蜜桃。
B.金粲选用木耳、火腿。
C.火珊选用金针菇、土豆。
D.水仙选用木耳、土豆。
E.土润选用水蜜桃、火腿。
55.【解析】选 B。
如果水仙选用土豆,7 题已推出水仙选了金针菇,则可知水仙选的两种就是金针
菇和土豆;由 7 题还可知:火珊选了木耳、土豆;木心、土润选了水蜜桃;综合
这些可知:金粲已不能选金针菇,金粲只能选木耳、火腿,显然 B 正确。
方法二:画表排除
人 金 木 水 火 土
菜 ---------------------
金 × × √ × √
木 × × √ √ ×
水 × √ × × √
火 √ √ × × ×
土 √ × × √ × ↩︎排序题
某厨艺大赛,要求厨师制作热菜、凉菜各一项,结果评定为“上品”、“中品”、“下品”3种。如果甲厨师每项结果不低于乙厨师,且至少有一项比乙厨师高,则称“甲厨师比乙厨师技艺高”(两个菜都高;一个菜一样,一个菜高)。现有厨师若干,他们之中没有一个比另一个技艺高,并且没有任意两人热菜结果一样,凉菜结果也一样的。满足上述条件的厨师最多能有多人?
A.无法确定
B.9人
C.6人
D.3人
E.2人
排除法:
B.9人,将9种情况占了,有两个“上品”和“下品”,一定可以分出高低。
①有一样相同,如果另一样也同。∵“没有任意两人热菜结果一样”,所以不可能。
②有一样相同,如果另一样不同。得:可直接分出高低,不符合题意,错误。①②得:有一样相同是不可能,∴所有人两样菜结果都不同
热菜 凉菜
A上 下
B中 中
C下 上
选D ↩︎5-6 题基于以下题干
某公司甲、乙、丙、丁、戊,5 人爱好出国旅游。去年,在日本,韩国,英国和法国 4 国中,他们每人都去了其中的两个国家旅游,且每个国家总有他们中的
2~3 人去旅游(∵(3)英法都有2人去过,所以(2)丙和戊不去英法,故丙戊去日韩),已知:
(1)如果甲去韩国,则丁不去英国;(5题:甲韩→丁非英)(6题:已知丁英→甲非韩→甲去日)
(2)丙与戊去年总是结伴出国旅游;(5题:丙=戊) (6题:去四人次亚,因为丙戊分别去过日韩)
(3)丁和乙只去欧洲国家旅游。(5题:丁英法、乙英法)(6题:去四人次欧,因为丁乙分别去过英法)
5.根据以上信息,可以得出以下哪项?
A.甲去了韩国和日本。
B.乙去了英国和日本。
C.丙去了韩国和英国。
D.丁去了日本和法国。
E.戊去了韩国和日本。
5.【解析】选 E。
①因为丁和乙只去欧洲国家旅游,且每人都去了其中的两个国家旅游,所以丁去
了英国和法国,乙去了英国和法国;又每个国家总有他们中的 2~3 人去旅游,
所以,丙与戊不去英国也不去法国;②由“丁去英国”结合条件(1)得,甲不去
韩国,所以,丙与戊都去了韩国,又丙与戊不去英国也不去法国,所以丙与戊还
去了日本。结合选项可得“戊去了韩国和日本”。
6.如果 5 人去欧洲国家旅游的总人数与去亚洲国家的一样多(欧洲5人,亚洲5人),则可以得出以下哪项?
A.甲去了日本。
B.甲去了英国。
C.甲去了法国。
D.戊去了英国。
E.戊去了法国。
6.【解析】选 A。
结合 5 题推理思路,若 5 人去欧洲国家旅游的总人次与去亚洲国家的一样多,则
甲去的国家不能既是英国又是法国,所以,甲一定去日本。 ↩︎44-46基于以下题干:
在某次听证会上,J、K、L、T、U、X、Y和Z八位与会者入座位置如下图所示:
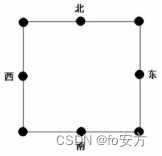
其中,J、K、L是民营企业代表,X、Y、Z是国营企业代表,T、U是官方代表。
以下条件成立:
(1)民营企业代表的座位是连着的,即任何一个民营企业代表的领座,至少有一位是另一个民营企业代表,国营企业代表的座位也是如此。
(2)没有一个民营企业代表和国营企业代表领座。(关键条件:需要T、U官方代表将民营代表和国营代表隔开)
(3)T的座位是东南角。
(4)J的座位在北排的中间。
(5)如果T和X领座,则T不和L领座。
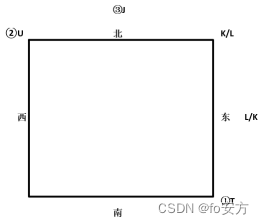
44.以下各项一定为真,除了(A)
A.西北角是国企(西北角是官方代表)
B.东北角是民企
C.西南角是国企
D.东边居中是民企
E.西边居中是国企
45.如果Y在西边居中,则以下哪两位代表不能都坐在拐角?
A.K和X
B.K和Z
C.L和U
D.L和X
E.L和Z
(1)条件的矛盾命题不可能出现:T、X邻且T、L邻。必假。
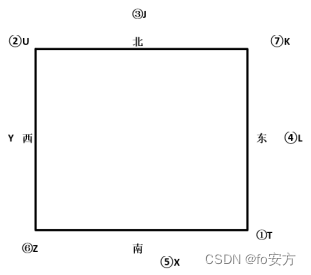
如果T、X邻且T、L邻,那么K、Z在拐角为假。
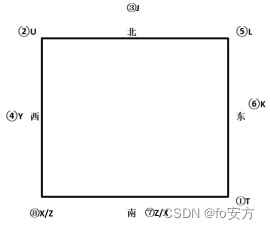
46.如果Y比L更靠南,但比T更靠北,则以下各项的两个代表都一定是领座,除了
A.J和K
B.K和T
C.T和X
D.U和Y
E.X和Z
解析:Y比L更靠南,但比T更靠北:Y在正西边。此时,L在Y南方,即为西南角。∵JKL连着,所以K在正东。T与X不能确定。
 ↩︎
↩︎2.某公司为员工免费提供菊花、绿茶、红茶、咖啡和大麦茶 5 种饮品。现有甲、乙、丙、丁、戊 5 为员工,他们每人都只喜欢其中的 2 种饮品,且每种饮品都只有 2 人喜欢,已知:
(1)甲和乙喜欢菊花,且分别喜欢绿茶和红茶中的一种;
(2)丙和戊分别喜欢咖啡和大麦茶中的一种。
根据上述信息,可以得出以下哪项?
A.甲喜欢菊花和绿茶。
B.乙喜欢菊花和红茶。
C.丙喜欢红茶和咖啡。
D.丁喜欢咖啡和大麦茶。
E.戊喜欢绿茶和大麦茶。
2.【解析】选 D。
根据条件(1)得到甲乙一定不选择“咖啡和大麦”;根据(2)得到“丙和戊分别喜欢咖啡和大麦茶中的一种”;又知“他们每人都喜欢其中的两种饮品,且每种饮品都只有 2 人喜欢”。得到 D 丁喜欢咖啡和大麦茶。
秒杀:条件没提及的对象,选项选没有提及的对象。选D。
方法一:排除法:
咖啡:由(1)得:非甲、非乙;由(2)得:非丙或非戊;∵“每种饮品都只有2人喜欢”,所以包括丁。
大麦:由(1)得:非甲、非乙;由(2)得:非丙或非戊。∵“每种饮品都只有2人喜欢”,所以包括丁。 ↩︎配对题-难题
3-4 题基于以下题干
放假 3 天,小李夫妇除安排一天休息之外,其他两天准备 6 件事:①购物(这件事编号为①,其他依次类推);②看望双方父母;③郊游;④带孩子去游乐场;
⑤去市内公园;⑥去影院看电影。他们商定:
(1)每件事均做一次,且在 1 天内做完,每天至少做两件事;
(2)④和⑤安排在同一天完成;
(3)②在③之前 1 天完成。(突破口:第一天、第二天、第三天,中“第二天”不可能休息,否则不存在“前1天”的情况。)
3.如果③和④安排在假期的第 2 天,则以下哪项是可能的?
A.①安排在第 2 天。(①在第一天,在第二天都可能)
B.②安排在第 2 天。 (与(3)矛盾)
C.休息安排在第 1 天。与(3)矛盾
D.⑥安排在最后一天。 第三天休息矛盾
E.⑤安排在第一天。与(2)矛盾
3.【解析】选 A。
如果③和④安排在第二天,根据条件(2),④和⑤安排在同一天完成,即:③④⑤
均在第二天;再根据条件(3),②在③之前一天完成,放假三天,一天休息,6
件事需要两天做完,即:②在第一天;又根据条件(1)每天至少做两件事,所以
①、⑥至少有一个在第一天,如果⑥在第一天,①可以在第二天。
方法一:
1 2 3
② ③ 休
④
⑤
4.如果假期第 2 天只做⑥等 3 件事,则可以得出以下哪项?
A.②安排在①的前一天。
B.①安排在休息一天之后。
C.①和⑥安排在同一天。(符合两种情况)
D.②和④安排在同一天。
E.③和④安排在同一天。
4.【解析】选 C。
放假三天,一天休息,6 件事需两天完成,如果假期第二天只做⑥等 3 件事,则
完成 6 件事的两天,每天做 3 件事;根据条件(3),②在③之前 1 天完成,即:
②在第一天、③在第二天;
第二天已经确定两件事,根据条件(2),④和⑤
安排在同一天完成,则④和⑤只能在第一天,即:②④⑤在第一天;(3)剩下
①和③⑥都在第二天。所以正确答案为 C 项。
方法一:
如果是第三天休息:
一 二 三
② ⑥ 休
④ ③
⑤ ①
如果是第一天休息:
一 二 三
休 ⑥ ③
② ④
① ⑤ ↩︎