A题直接枚举即可，枚举日期，暴力匹配

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
bool check(string t){if(t.substr(0, 4)!="2023") return false;string mon = t.substr(4, 2);string day = t.substr(6, 2);int m = (mon[0]-'0')*10+(mon[1]-'0');int d = (day[0]-'0')*10+(day[1]-'0');if(m==1||m==3||m==5||m==7||m==8||m==10||m==12){if(d>=1&&d<=31) return true;}else if(m==2){if(d>=1&&d<=28) return true;}else if(m==4||m==6||m==9||m==11){if(d>=1&&d<=30) return true;}return false;
};string p="",s="";
int ans = 0, n;string mon[]={"01","02","03","04","05","06","07","08","09","10","11","12"};
string day[]={"01","02","03","04","05","06","07","08","09","10",
"11","12","13","14","15","16","17","18","19","20",
"21","22","23","24","25","26","27","28","29","30","31"};
int md[]={31,28,31,30,31,30,31,31,30,31,30,31};bool check(string t,string s){int j=0;for(int i=0;i<t.size();++i){if(j==s.size()) return true;if(t[i]==s[j]) j++;}return j==s.size();
}void solve(){while(cin >> s){p += s;}// cout << p << endl;n=p.size();string t = "2023";for(int i=0;i<12;++i){for(int j=0;j<md[i];++j){string N = t + mon[i] + day[j];if(check(p, N)) {ans ++;}}}cout<<ans<<endl;
}int main(){solve();return 0;
}

答案：

可以看出香浓信息熵有单调性(在0不超过1这个前提下)
因此直接二分即可，顺便输出一下结果对应的函数值

#include<bits/stdc++.h>
using namespace std;
#define int long long
double p(int x,int y){ //x 0 y 1double P0 = 1.0*x/(x+y);double P1 = 1.0*y/(x+y);return -1.0*x*x/(x+y)*log2(P0)-1.0*y*y/(x+y)*log2(P1);
}void solve(){int n = 23333333;int l=1, r=(n-1)/2;double PP = 11625907.5798;while(l<r){int mid = (l+r)>>1;double t = p(mid, n-mid);if(t<PP) l=mid+1;else r=mid;}cout << l << endl;l=11027421;printf("%.5lf", p(l, n-l));
}signed main(){solve();return 0;
}

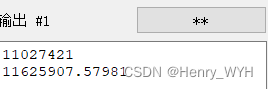
貌似可以直接O(1)算，但是我选择直接二分

二分的正确性在保证有解的前提下成立

#include<iostream>
#include<vector>
using namespace std;
//V:normal -> 1:X
void solve(){int n;cin >> n;long long x,y,X=1e9,Y=0;vector<pair<int,int>> vec;for(int i=0;i<n;++i){cin >> x >> y;vec.push_back({x,y});}auto check=[&](long long x)->bool{for(auto u:vec){if(u.first/x < u.second) return false;}return true;};long long l=1,r=1e9;while(l<r){long long mid=(l+r+1)>>1;if(check(mid)) l=mid; // x/mid >= yelse r=mid-1;}Y=l;auto find=[&](long long x)->bool{for(auto u:vec){if(u.first/x > u.second) return false;}return true;};l=1,r=1e9;while(l<r){long long mid=(l+r)>>1;if(find(mid)) r=mid;else l=mid+1;}X=l;cout<<X<<" " << Y<<endl;
}int main(){solve();return 0;
}

顺便跑了几组对拍：

N $\le$ 10 直接搜，不要想什么贪心

#include<iostream>
#include<vector>
#include<array>
using namespace std;bool vis[20];
int n;bool dfs(int num,int now, vector<array<int,3>>& vec){if(num==n){return true;}int flag = 0;for(int i=0;i<n;++i){if(!vis[i]){if(now>vec[i][0]+vec[i][1]) return false;vis[i] = true;flag |= dfs(num+1, now+vec[i][2], vec);vis[i]=false;}}return flag;
}void solve(){cin >> n;for(int i=1;i<=n;++i) vis[i] = 0;vector<array<int,3>> vec;for(int i=0;i<n;++i){int x,y,z;cin >> x >> y >> z;vec.push_back({x,y,z});}bool res = dfs(0, 0, vec);cout<<(res?"YES":"NO")<<"\n";
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; cin >>_;while(_--) solve();return 0;
}
/*
2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20
*/

删最少数使得他是接龙序列，即求原序列的最大接龙子序列，然后用n减去。
最大接龙子序列求法：DP
但是我们发现转移类型一共只有9种1~9结尾的数字
因此我们可以开一个数组f[i]表示前i个数字，以第i个结尾的最大接龙子序列。
再开一个数组bac[1~9]表示 以1~9结尾的最大接龙子序列
每次用第i个数组开头的字母对应的数组更新f[i]，然后再用f[i]反过来更新bac即可
细节看代码

#include<iostream>
#include<vector>
#include<array>
#include<string>
using namespace std;int n;void solve(){cin >> n;vector<string> vec;for(int i=0;i<n;++i){string t;cin >> t;vec.push_back(t); }vector<int> bac(10); //1,2,3....vector<int> f(n+1, 0);int ans = 0 ;for(int i=0;i<n;++i){f[i]=max(1, bac[vec[i][0]-'0']+1);ans=max(ans, f[i]);bac[vec[i].back()-'0'] = max(bac[vec[i].back()-'0'], f[i]);}cout << n-ans << endl;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; // cin >>_;while(_--) solve();return 0;
}

先用边缘的海水进行bfs求出"真的海水"，然后再对所有岛屿进行BFS,此时BFS的时候非真的海水可以直接识别为陆地然后入队。
两遍BFS得到答案。

#include<iostream>
#include<vector>
#include<array>
#include<string>
#include<queue>
#define x first
#define y second
using namespace std;int n,m;
char G[60][60];
int vis[60][60], g[60][60], water[60][60];int d[][2]={1,0,0,1,-1,0,0,-1};
int mov[][2]={{1,0},{-1,0},{0,1},{0,-1},{1,-1},{1,1},{-1,-1},{-1,1}};void solve(){cin >> n >> m;for(int i=1;i<=n;++i){for(int j=1;j<=m;++j){vis[i][j] = g[i][j] = water[i][j] = 0;}}for(int i=1;i<=n;++i){cin >> (G[i]+1);for(int j=1;j<=m;++j){g[i][j] = G[i][j]-'0';}}queue<pair<int,int>> q;for(int i=1;i<=n;++i){if(g[i][1] == 0){water[i][1] = true;q.push({i, 1});}if(g[i][m] == 0){water[i][m] = true;q.push({i, m});}}for(int i=1;i<=m;++i){if(g[1][i] == 0){if(!water[1][i]){water[1][i] = true;q.push({1, i});}}if(g[n][i] == 0){if(!water[n][i]){water[n][i] = true;q.push({n, i});}}}while(q.size()){auto u=q.front(); q.pop();int x=u.x,y=u.y;for(int i=0;i<8;++i){int xx=x+mov[i][0], yy=y+mov[i][1];if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!water[xx][yy]&&!g[xx][yy]){q.push({xx, yy});water[xx][yy] = true;}}}while(q.size()) q.pop();int idx = 0;for(int i=1;i<=n;++i){for(int j=1;j<=m;++j){if(!water[i][j]&&g[i][j]&&!vis[i][j]){q.push({i, j});vis[i][j]=++idx;while(q.size()){auto u=q.front(); q.pop();int x=u.x,y=u.y;for(int i=0;i<4;++i){int xx=x+d[i][0], yy=y+d[i][1];if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!vis[xx][yy]&&!water[xx][yy]){vis[xx][yy]=idx;q.push({xx,yy});}}}}}}cout << idx << endl;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; cin >>_;while(_--) solve();return 0;
}/*
2
5 5
01111
11001
10101
10001
11111
5 6
111111
100001
010101
100001
111111
*/

二分/双指针都行
先按照位置处理出来两个数组
然后枚举开头的位置，二分出结尾在另一个数组的合法位置，直接累加答案

#include<iostream>
#include<vector>
#include<array>
#include<string>
#include<queue>
#define x first
#define y second
using namespace std;int k;
char st,ed;
string p;void solve(){cin >> k;cin >> p >> st >> ed;vector<int> ps,pe;for(int i=0;i<p.size();++i){if(p[i]==st) ps.push_back(i);if(p[i]==ed) pe.push_back(i);}long long ans = 0;for(int i=0;i<ps.size();++i){int x = ps[i];int X = x + k - 1;int l=0,r=pe.size()-1;while(l<r){int mid=(l+r)>>1;if(pe[mid] >= X) r=mid;else l=mid+1;}if(pe[l] >= X){ans += pe.size() - l;}}cout<<ans<<endl;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; // cin >>_;while(_--) solve();return 0;
}

双链表维护每个数左边和右边分别是什么数
set维护每个位置的值和要删的最小值
本题考察STL的用法

#include<iostream>
#include<vector>
#include<algorithm>
#include<array>
#include<string>
#include<queue>
#include<set>
#define x first
#define y second
using namespace std;int n,k;void solve(){cin >> n >> k;vector<int> a(n+1),pre(n+1),nxt(n+1);set<pair<int,int>> ds;for(int i=1;i<=n;++i){pre[i] = i-1;nxt[i] = i+1;}for(int i=1;i<=n;++i){cin >> a[i];ds.insert({a[i], i});}for(int t=1;t<=k;++t){auto pos=ds.begin();int x=pos->first, y=pos->second;int l = pre[y], r = nxt[y];ds.erase(pos);pre[nxt[y]]=pre[y];nxt[pre[y]]=nxt[y];pre[y]=-1, nxt[y]=-1;if(l>0){ds.erase(ds.find({a[l], l}));a[l] += x;ds.insert({a[l], l});}if(r<=n){ds.erase(ds.find({a[r], r}));a[r] += x;ds.insert({a[r], r});}}vector<pair<int,int>> temp;for(auto u:ds){temp.push_back({u.y, u.x});}sort(temp.begin(), temp.end());for(auto u:temp){cout << u.y << " ";}cout<<"\n";
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; // cin >>_;while(_--) solve();return 0;
}

LCA, 没啥好说的

#include<iostream>
#include<vector>
#include<array>
#include<string>
#include<queue>
#define x first
#define y second
using namespace std;
#define debug(x) cout<<#x<<": "<<x<<endl
#define N 100010
vector<pair<int,int>> edge[N];
int n,m,k;
int dep[N],fa[20][N];
int rout[N];
queue<int> q;void bfs(){for(int i=1;i<=n;++i) dep[i]=-1;dep[1]=0;q.push(1);while(q.size()){auto u=q.front(); q.pop();for(auto v:edge[u]){int ver = v.x, w=v.y;if(dep[ver]==-1){dep[ver] = dep[u] + w;q.push(ver);fa[0][ver] = u;for(int i=1;i<=19;++i){fa[i][ver] = fa[i-1][fa[i-1][ver]];}}}}
}int lca(int x,int y){if(dep[x] < dep[y]) swap(x, y);for(int i=19;i>=0;--i){if(dep[fa[i][x]] >= dep[y])x = fa[i][x];}if(x==y) return x;for(int i=19;i>=0;--i){if(fa[i][x]!=fa[i][y])x=fa[i][x], y=fa[i][y];}return fa[0][x];
}int dist(int x,int y){return dep[x]+dep[y]-2*dep[lca(x,y)];
}void solve(){cin >> n >> k;for(int i=1;i<n;++i){int x,y,z;cin >> x >> y >> z;edge[x].push_back({y, z});edge[y].push_back({x, z});}bfs();vector<int> a(k+1);for(int i=1;i<=k;++i){cin >> a[i];}int now = a[1];long long time = 0;for(int i=1;i<=k;++i){time += dist(now, a[i]);now = a[i];}cout << time - dist(a[1], a[2]) << " ";now = a[1];for(int i=2;i<=k;++i){int temp = time;temp -= dist(now, a[i]);if(i!=k){temp -= dist(a[i], a[i+1]);temp += dist(now, a[i+1]);}cout << temp << " ";now = a[i];}cout << "\n";
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; // cin >>_;while(_--) solve();return 0;
}
/*
6 4
1 2 1
1 3 1
3 4 2
3 5 2
4 6 3
2 6 5 1
*/

树上差分，也是LCA，最后再DFS一下

#include<iostream>
#include<vector>
#include<array>
#include<string>
#include<queue>
#define x first
#define y second
using namespace std;
#define debug(x) cout<<#x<<": "<<x<<endl
#define N 100010int n,m,k;
vector<int> edge[N];
pair<int,int> p[N];
int w[N],dep[N],fa[20][N];
pair<int,int> edges[N];void bfs(){for(int i=1;i<=n;++i) dep[i]=-1;queue<int> q;q.push(1);dep[1]=1;while(q.size()){auto u=q.front(); q.pop();for(auto v:edge[u]){if(dep[v]==-1){dep[v]=dep[u]+1;q.push(v);fa[0][v] = u;for(int i=1;i<=19;++i)fa[i][v]=fa[i-1][fa[i-1][v]];}}}
}int lca(int x,int y){if(dep[x]<dep[y]) swap(x, y);for(int i=19;i>=0;--i){if(dep[fa[i][x]] >= dep[y])x=fa[i][x];}if(x==y) return x;for(int i=19;i>=0;--i){if(fa[i][x]!=fa[i][y])x=fa[i][x], y=fa[i][y];}return fa[0][x];
}int f[N];void dfs(int u,int pre){f[u] = w[u];for(auto v:edge[u]){if(v!=pre){dfs(v, u);f[u] += f[v];}}
}void solve(){cin >> n >> m;for(int i=1;i<n;++i){int x,y;cin >> x >> y;edge[x].push_back(y);edge[y].push_back(x);edges[i] = {x, y};}bfs();for(int i=1;i<=m;++i){cin >> p[i].x >> p[i].y;w[p[i].x] ++, w[p[i].y] ++;w[fa[0][lca(p[i].x, p[i].y)]] -= 1;w[lca(p[i].x, p[i].y)] -= 1;}dfs(1, -1);int ans = -1;for(int i=1;i<n;++i){int x=edges[i].x, y=edges[i].y;if(dep[x]<dep[y]) swap(x, y);//y-xif(f[x]==m){ans=max(ans, i);}}cout<<ans<<endl;
}int main(){ios::sync_with_stdio(false);cin.tie(0);int _=1; // cin >>_;while(_--) solve();return 0;
}