题目

小明开了一家糖果店。

他别出心裁：把水果糖包成4颗一包和7颗一包的两种。

糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。

当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。

大于17的任何数字都可以用4和7组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式

两个正整数 n,m，表示每种包装中糖的颗数。

输出格式

一个正整数，表示最大不能买到的糖数。

数据范围

2≤n,m≤1000，

保证数据一定有解。

输入样例：

4 7

输出样例：

思路

这题一眼能看出来，肯定有个数学结论，但咱不是专业打ACM的真不知道啊，两种思路：

暴力模拟
打表猜数学公式

看难度也知道这题肯定不是后面的题，蓝桥里面估计就是个10分题，时空应该不会为难我们。

再瞄一眼范围，果真如此。

那就暴力模拟。（hhhhh主要是真让我猜公式可能也猜不明白）

因为是整数，所以认定所有可能的取值为[0, 1000*10000]内所有的整型数据，被取到过的标记下1。

一共有 N 个数字就 N 轮循环，每轮循环继承上一轮的结果；并且将已存在的数 ±a[i] 的数也标注为1。

最后统计下 1 的个数。

注意点：

判断数据范围，免得 ± 的时候段错误。
好像就没了，毕竟是道简单练手题。

结论：

这里有个公式记一下 m*n-(m+n)=>两个数 ± 所不能表示的最大的数。

拿 3 和 8 举例（结论是普适的）
在这里插入图片描述

假设 n 是小的那个数，m 是大的那个数，很容易发现[(n-1)m ,nm] 间的数会被填满，因为 0m -> nm 之间的每个序列其实就相当于 0*m 的那段序列（白色序列）的平移，而且每次平移不重合。

所以：

在 [(n-1)m ,nm] 那段刚好凑齐了 n 种不同的间隔为 n 的序列，所以这段的数字都能取到。

在 [(n-1)m ,nm] 之后的区间的情况同 [(n-1)m ,nm] 区间，所以全都能取到。

在 [(n-1)m ,nm] 之前的第一组区间 [(n-2)m, (n-1)m] 每隔n个数都会缺一个。

所以最后缺的是 (n-1)m - x ，这个 x 应该怎么定？因为最后的序列是由 (n-1)m+kn 决定的，所以 (n-1)m -kn* 都是空缺的，所以 x==n。

所以

最后缺的那个就是 (n-1)m - n 位置。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1000*10000+5;
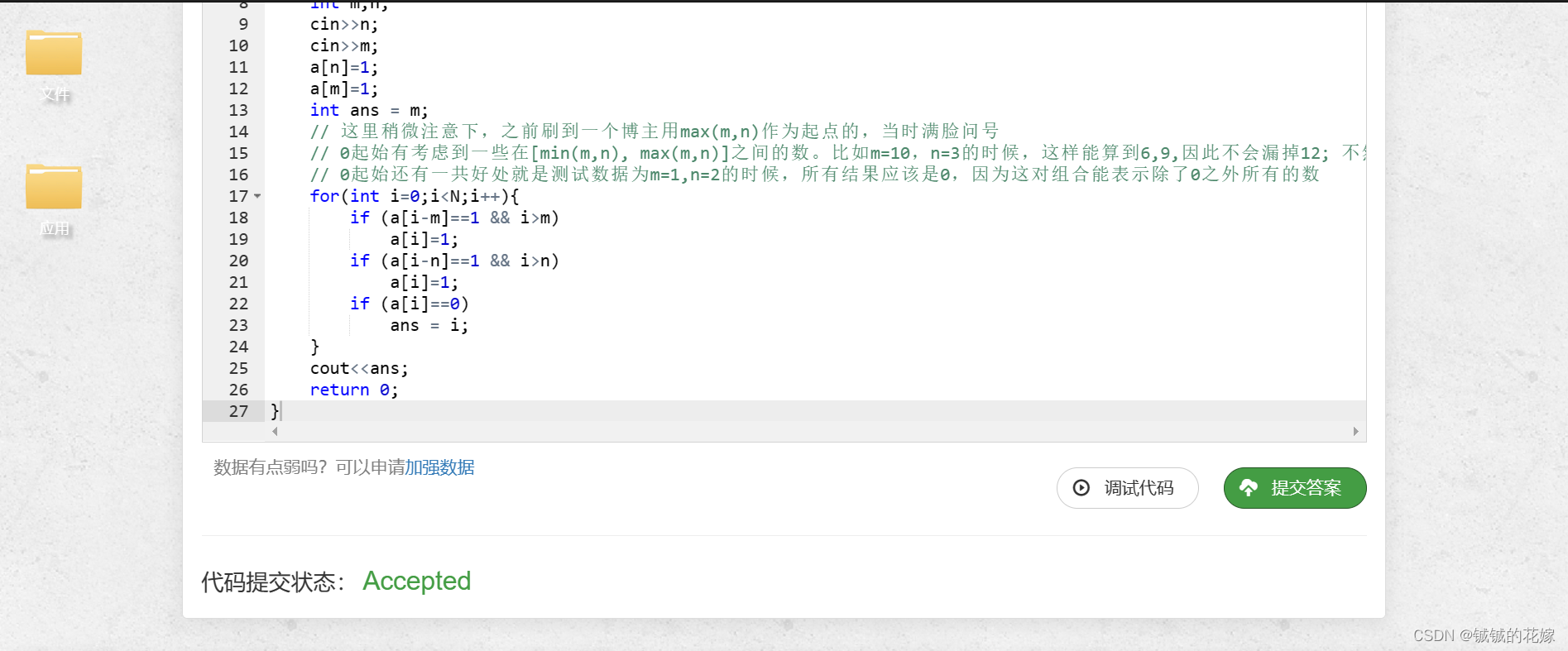
int a[N];int main(){memset(a, 0, sizeof(a));int m,n;cin>>n;cin>>m;a[n]=1;a[m]=1;int ans = m;// 这里稍微注意下，之前刷到一个博主用max(m,n)作为起点的，当时满脸问号// 0起始有考虑到一些在[min(m,n), max(m,n)]之间的数。比如m=10，n=3的时候，这样能算到6,9,因此不会漏掉12; 不然max(m,n)起点直接漏了6,9以及后面相关的数据// 0起始还有一共好处就是测试数据为m=1,n=2的时候，所有结果应该是0，因为这对组合能表示除了0之外所有的数for(int i=0;i<N;i++){if (a[i-m]==1 && i>m)a[i]=1;if (a[i-n]==1 && i>n)a[i]=1;if (a[i]==0)ans = i;}cout<<ans;return 0;
}