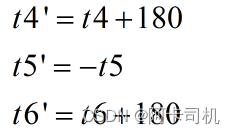puma560机器人D-H参数
puma560采用的是改进D-H参数,其DH参数表如下:
| i | αi | ai | di | θi |
| 1 | 0 | 0 | 0 | t1 |
| 2 | -90 | 0 | 0 | t2 |
| 3 | 0 | r2 | d3 | t3 |
| 4 | -90 | r3 | d4 | t4 |
| 5 | 90 | 0 | 0 | t5 |
| 6 | -90 | 0 | 0 | t6 |
对于参数为(α,a,d, θ)的机械臂,其变换矩阵为:
T = [ cosθ, -sinθ, 0, a;
sinθcosα, cosθcosα, -sinα, -dsinα;
sinθsinα, cosθsinα, cosα, dcosα;
0, 0, 0, 1]
所以可以根据上表写出6个关节变换矩阵:
T01 = [cos(t1),-sin(t1),0,0;
sin(t1),cos(t1),0,0;
0,0,1,0;
0,0,0,1];
T12 = [cos(t2),-sin(t2),0,0;
0,0,1,0;
-sin(t2),-cos(t2),0,0;
0,0,0,1];
T23 = [cos(t3),-sin(t3),0,r2;
sin(t3),cos(t3),0,0;
0,0,1,d3;
0,0,0,1];
T34 = [cos(t4),-sin(t4),0,r3;
0,0,1,d4;
-sin(t4),-cos(t4),0,0;
0,0,0,1];
T45 = [cos(t5),-sin(t5),0,0;
0,0,-1,0;
sin(t5),cos(t5),0,0;
0,0,0,1];
T56 = [cos(t6),-sin(t6),0,0;
0,0,1,0;
-sin(t6),-cos(t6),0,0;
0,0,0,1];
运动学正解
puma560机器人运动学正解计算为:
T06 = T01*T12*T23*T34*T45*T56,具体就不放结果了
运动学逆解
已知T06=[r11,r12,r13,Px;
r21,r22,r23,Py;
r31,r32,r33,Pz;
0, 0, 0, 1]
求出6个关节角t1,t2,t3,t4,t5,t6,就称之为运动学逆解
关节角t1计算
可以先计算T16 = T12*T23*T34*T45*T56,计算结果为:
T16 =
[-c23*(s4s6-c4c5c6)-s23s5c6, s23s5s6-c23(c6s4+c4c5s6),-s23c5-c23c4s5, r3c23-d4s23+r2c2;
-c4s6-s4c5c6, s4c5s6-c4c6, s4s5, d3;
s23(s4s6-c4c5c6)-c23s5c6, s23*(s4c6+c4c5s6)+c23s5s6, s23c4s5-c23c5, -d4c23-r3s23-r2s2;
0, 0, 0, 1]
这里的c23=cos(t2+t3),s23=sin(t2+t3),s2=sint2,s3=sin(t3),是一种缩写记法。
又有

由T16[1,3]元素相等 ,可得:
-s1Px+c1Py = d3
令
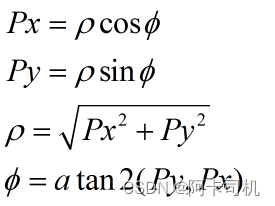
则有:
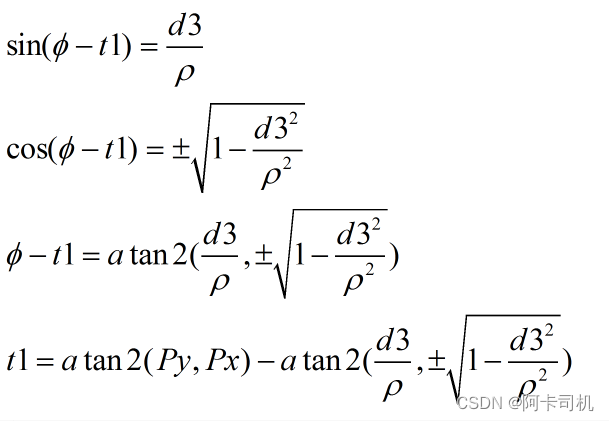
可以看到t1有2个解。
关节角t3计算
现在t1已知,根据T16的元素(0,3)、元素(1,3)、元素(2,3)列出等式:
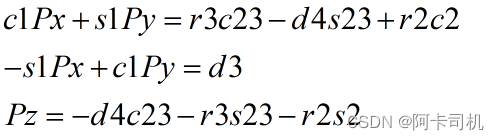
三式取平方和有:
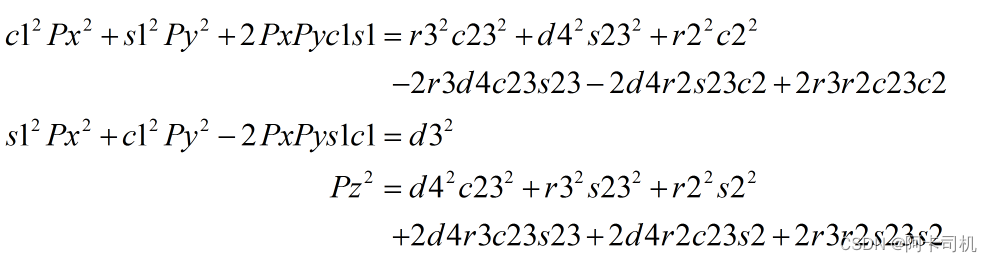
三式相加化简有:
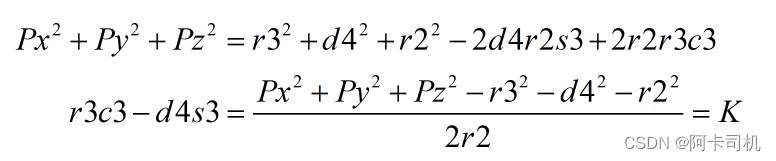
有看到了熟悉的式子,可以计算t3等于:
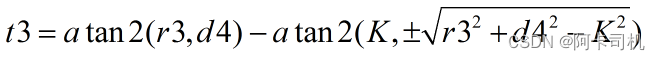
可以看到t3有2个解。
关节角t2的计算
先计算T03 ,建议用matlab符号运算来计算,matlab符号运算是推算公式的利器。
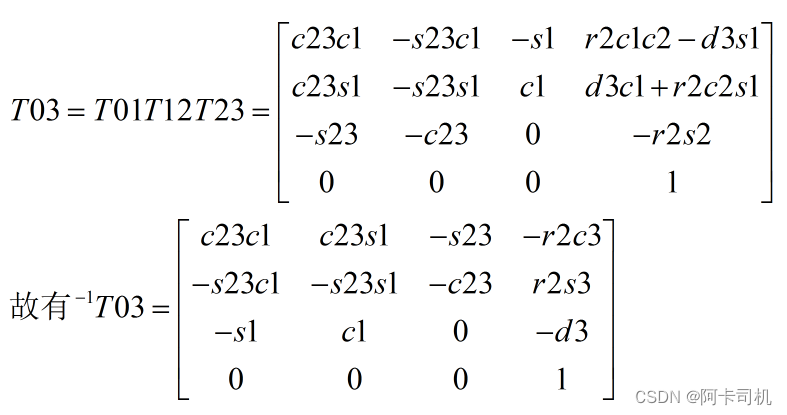
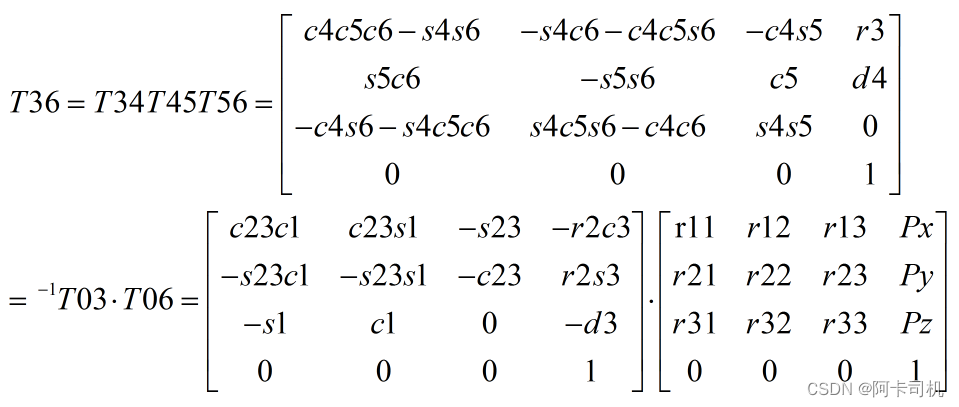
取T36的(0,3)元素及(1,3)元素列出等式:
c23c1Px+c23s1Py-s23Pz-r2c3 = r3
-s23c1Px-s23s1Py-c23Pz+r2s3 = d4
联立上面等式可以解出c23和s23,进而可以求出t2+t3,进而求出t2。
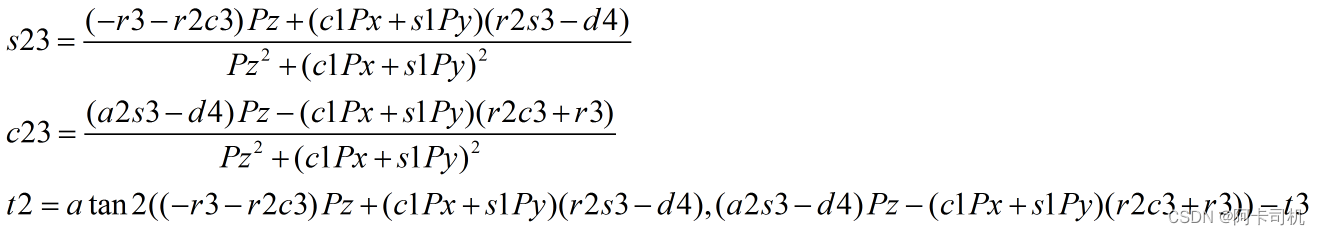
关节角t4的计算
T36矩阵中取(0,2)元素及(2,2)元素,成立等式:
r13c23c1+r23c23s1-r33s23 = -c4s5
-s1r13+c1r23 = s4s5
只要t5不为0,则有t4=atan2(-s1r13+c1r23,-r13c23c1-r23c23s1+r33s23);
当t5为0时,关节4和关节6出于一条直线,所有可能的接都是t4和t6的和或差。
关节角t5和t6的计算
先计算T04及T04的逆矩阵
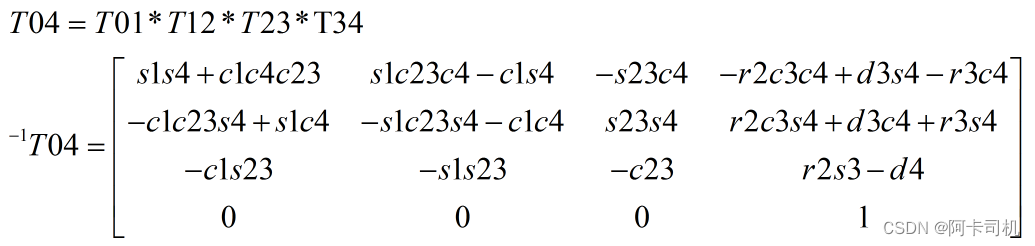
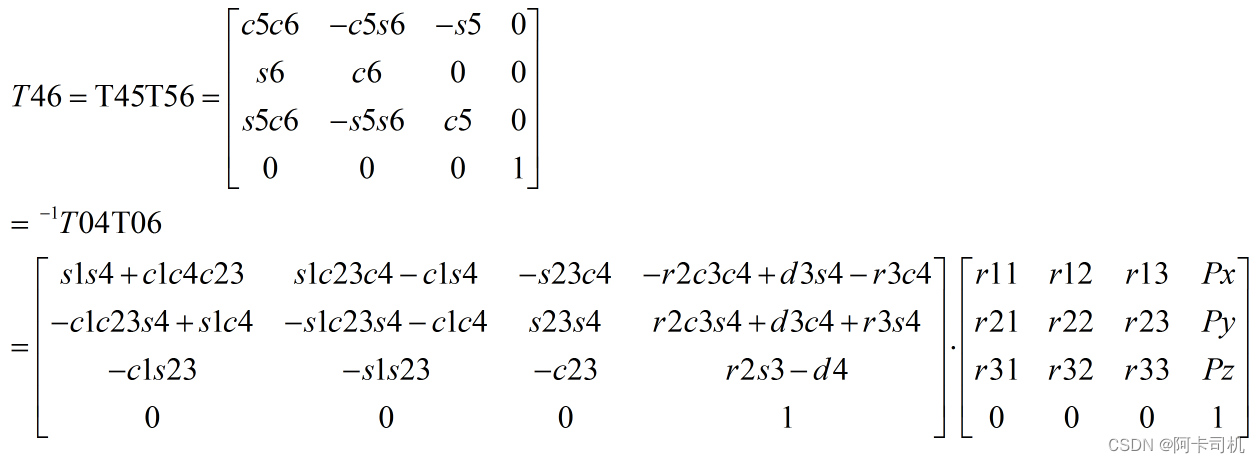
取T46的(0,2)元素和(2,2)元素构成等式:
-s5=r13(s1s4+c1c4c23)+r23(s1c23c4-c1s4)-r33s23c4
c5=-r13c1s23-r23s1s23+c1c4)-r33c23
故有t5=atan2(-(r13(s1s4+c1c4c23)+r23(s1c23c4-c1s4)-r33s23c4),-r13c1s23-r23s1s23+c1c4)-r33c23)
取T46的(1,0)元素和(1,1)元素构成等式:
s6 = r21(-c1c23s4+s1c4)+r21(-s1c23s4-c1c4)+r3123s4
c6=r12(-c1c23s4+s1c4)+r22(-s1c23s4-c1c4)+r32s23s4
求出t6=atan2(r21(-c1c23s4+s1c4)+r21(-s1c23s4-c1c4)+r3123s4,r12(-c1c23s4+s1c4)+r22(-s1c23s4-c1c4)+r32s23s4)
前面计算t1和t3各有2个解,所以共有4组解,再加上腕关节翻转,可以得出8组解。对于计算出的4组解,由腕关节翻转,可以得到: