目录
前言
一、函数定义与调用基本语法
1.函数定义语法
2.【例5.1.1】编写生成(不大于n)斐波那契数列的函数并调用
3.函数递归调用
(1)介绍
(2)【例5-2】使用递归法对整数进行因数分解
二、函数参数
1.位置参数
2.默认值参数
3.关键参数
4.可变长度参数
5.传递参数时的序列解包
三、变量作用域
四、lambda表达式
五、生成器函数设计要点
1.介绍
2.【例5-3】编写并使用能够生成斐波那契数列的生成器函数
前言
- 掌握函数定义和调用的用法
- 理解递归函数的执行过程
- 掌握位置参数、关键参数、默认参数和长度可变参数的用法
- 理解函数调用时参数传递的序列解包用法
- 理解变量作用域
- 掌握lamda表达式的定义与用法
- 理解生成器函数工作原理
一、函数定义与调用基本语法
1.函数定义语法
def 函数名([参数列表]):
'''注释'''
函数体
【注】
- 为何要定义函数:实现代码的复用、保证代码的一致性、复杂问题简化(任务分拆)等
- 函数形参不需要声明类型,也不需要指定函数返回值类型
- 即使该函数不需要接受任何参数,也必须保留一对空的圆括号
- 括号后面的冒号必不可少
- 函数体相对于def关键字必须保持一定的空格缩进
- python允许嵌套定义函数
2.【例5.1.1】编写生成(不大于n)斐波那契数列的函数并调用
- 斐波那契数列:0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181……
- 这个数列第0项是0,第1项是1,从第三项开始,每一项都等于前两项之和
- f(n)=f(n-1)+f(n-2),n=2,3……
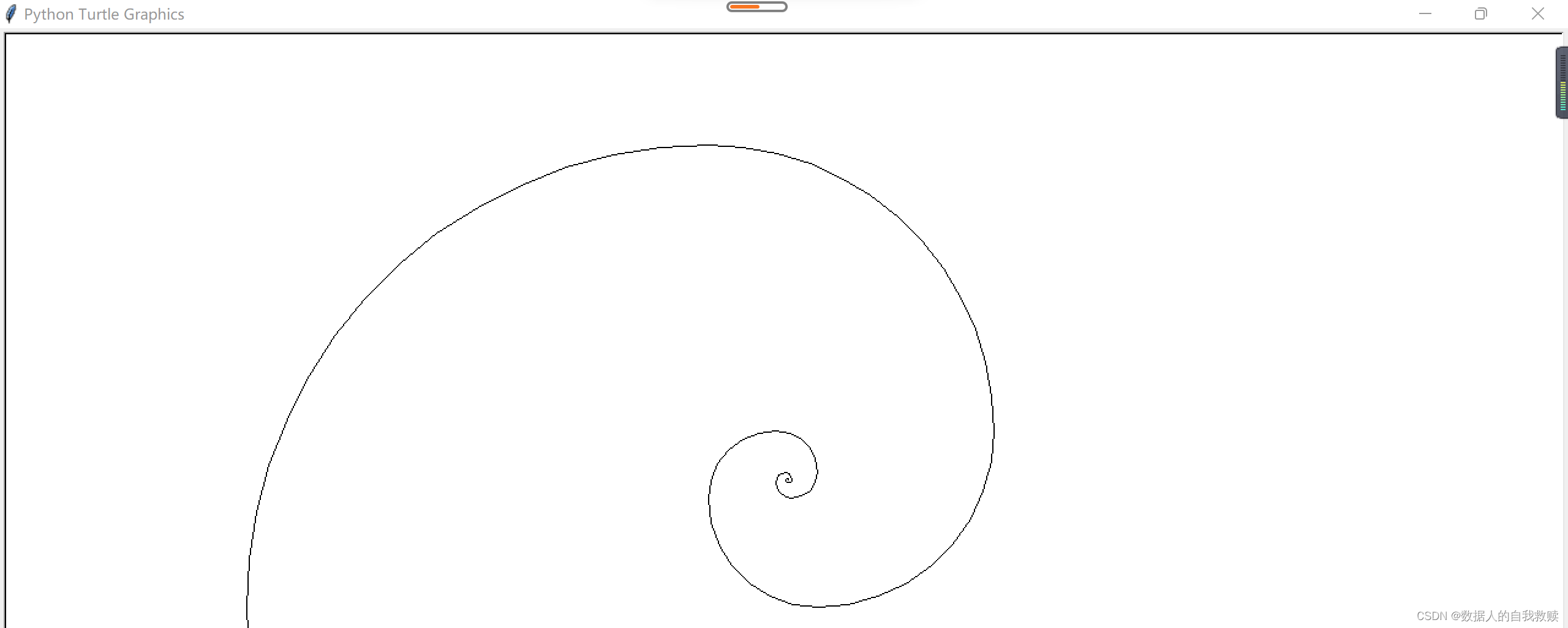
>>> import turtle
>>> a,b=0,1
>>> while a<1000:
... turtle.circle(a,90)
... a,b=b,a+b
...
...
>>> def fib(n):
... a,b=1,1
... while a<n:
... print(a,end=' ')
... a,b=b,a+b
... print()
...
...
>>> fib(100)
1 1 2 3 5 8 13 21 34 55 89
3.函数递归调用
(1)介绍
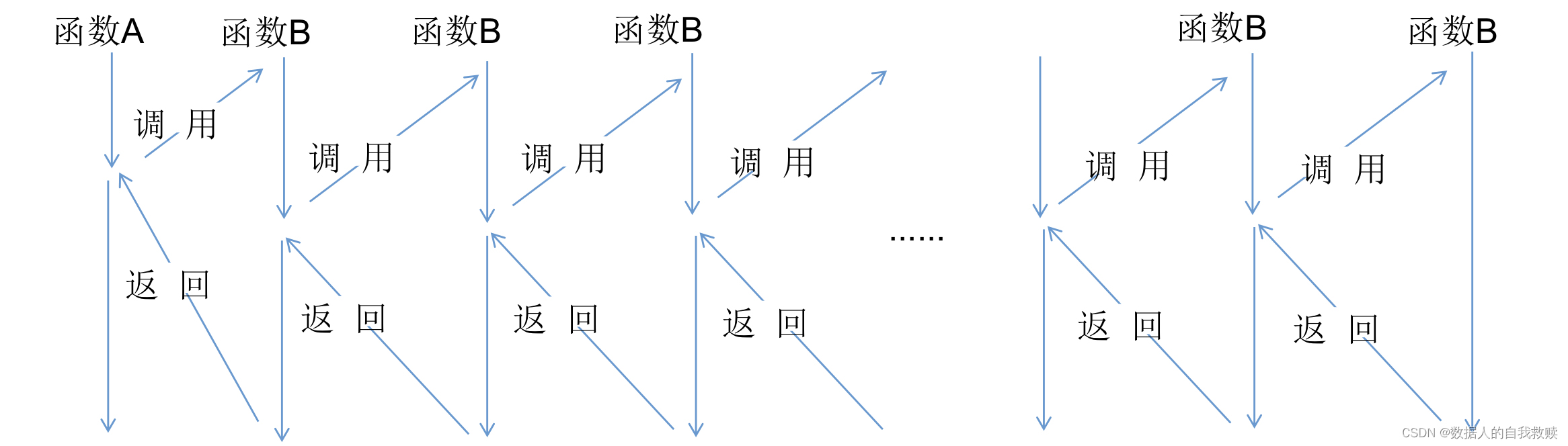
函数的递归调用是函数调用的一种特殊情况,函数调用自己,自己在调用自己,自己再调用自己……当某个条件得到满足的时候就不再调用了,然后再一层一层地返回直到该函数第一次调用的位置。
#计算第n个Fibonacci数
>>> def fib(n):
... a,b=0,1
... count=1
... while count<n:
... a,b=b,a+b
... count=count+1
... print(a)
...
...
>>> fib(10)
34
>>> def fib(n):
... if n==0 or n==1:
... return n
... else:
... return fib(n-1)+fib(n-2)
...
...
>>> fib(10)
55
(2)【例5-2】使用递归法对整数进行因数分解
>>> from random import randint
>>> def factors(num,fac=[]):
... #每次都从2开始查找因数
... for i in range(2,int(num**0.5)+1):
... #找到一个因数
... if num%i==0:
... fac.append(i)
... #对商继续分解,重复这个过程
... factors(num/i,fac)
... #注意,这个break非常重要
... break
... else:
... #不可分解了,自身也是个因数
... fac.append(num)
...
...
>>> fac=[]
>>> n=randint(2,10**8)
>>> factors(n,fac)
>>> result='*'.join(map(str,fac))
>>> if n==eval(result):
... print(n,'= '+result)
...
...
10666235 = 5*941*2267.0
二、函数参数
函数定义时圆括弧内是使用括号分隔开的形参列表(parameters),函数可以有多个参数,也可以没有参数,但定义和调用时一对圆括弧必须要有,表示这是一个函数并且不接受参数。
调用函数时向其传递实参(arguments),根据不同的参数类型,将实参的引用传递给形参。
定义函数时不需要声明参数类型,解释器会根据实参的类型自动推断形参的类型。
1.位置参数
位置参数(positional arguments)是比较常用的形式,调用函数时实参和形参的顺序必须严格一致,并且实参和形参的数量必须相同。
>>> def demo(a,b,c):
... print(a,b,c)
...
...
>>> demo(3,4,5) #按位置传递参数
3 4 5
>>> demo(3,5,4)
3 5 4
>>> demo(1,2,3,4) #实参与形参数量必须相同
Traceback (most recent call last):File "<pyshell#57>", line 1, in <module>demo(1,2,3,4)
TypeError: demo() takes 3 positional arguments but 4 were given
2.默认值参数
在调用带有默认值参数的函数时,可以不用为设置了默认值的形参进行传值,此时函数将会直接使用函数定义时设置的默认值,当然也可以通过显式赋值来替换其默认值。在调用函数时是否为默认值参数传递实参是可选的。
需要注意的是,在定义带有默认值参数的函数时,任何一个默认值参数右边都不能再出现没有默认值的普通位置参数,否则会提示语法错误。
带有默认值(事先给形参赋的值)参数的函数定义语法如下:
def 函数名(……,形参名=默认值):
函数体
>>> def say(message,times=1):
... print((message+' ')*times)
...
...
>>> say('hello')
hello
>>> say('hello',3)
hello hello hello
3.关键参数
关键参数主要指调用函数时的参数传递方式(调用函数时给出参数名(关键参数),传递实参就与顺序无关了!)与函数定义无关。通过关键参数可以按参数名字传递值,明确指定哪个值传递给哪个参数,实参顺序可以和形参顺序不一致,但不影响参数值的传递结果,避免了用户需要牢记参数位置和顺序的麻烦,使用函数的调用和参数传递更加灵活方便。
>>> def demo(a,b,c=5):
... print(a,b,c)
...
...
>>> demo(3,7)
3 7 5
>>> demo(c=8,a=0,b=9)
0 9 8
4.可变长度参数
可变长度参数主要有两种形式:在参数名前加1个*或2个**
- *parametre用来接收多个位置参数并将其放在一个元组中
>>> def demo(*p):
... print(p)
...
...
>>> demo(1,2,3)
(1, 2, 3)
>>> demo(1,2)
(1, 2)
>>> demo(1,2,3,4,5,6,7,8)
(1, 2, 3, 4, 5, 6, 7, 8)
- **parametre接收多个关键参数并存放到字典中
>>> def demo(**p):
... for item in p.items():
... print(item)
...
...
>>> demo(x=12,y=11,z=10)
('x', 12)
('y', 11)
('z', 10)
5.传递参数时的序列解包
传递参数时,可以通过在实参序列前加一个星号将其解包,然后传递给多个单变量形参。
>>> def demo(a,b,c):
... print(a+b+c)
...
...
>>> seq=[1,2,3]
>>> demo(*seq)
6
>>> tup=(1,2,3)
>>> demo(*tup)
6
>>> dic={1:'a',2:'b',3:'c'}
>>> demo(*dic)
6
>>> set1={1,2,3}
>>> demo(*set1)
6
>>> demo(*dic.values())
abc
如果函数实参是字典,可以在前面加两个星号进行解包,等价于关键参数。
>>> def demo(a,b,c):
... print(a+b+c)
...
...
>>> dic={'a':1,'b':2,'c':3}
>>> demo(**dic)
6
>>> demo(a=1,b=2,c=3)
6
>>> demo(*dic.values())
6
三、变量作用域
变量起作用的代码范围称为变量的作用域,不同作用域内变量名可以相同,互不影响。
在函数内部定义的普通变量只在函数内部起作用,称为局部变量。当函数执行结束后,局部变量自动删除,不再可以使用。
局部变量的引用比全局变量速度快,应优先考虑使用。
全局变量可以通过关键字global来定义。这分为两种情况:
- 一个变量已在函数外定义,如果在函数内需要为这个变量赋值,并要将这个赋值结果反映到函数外,可以在函数内使用global将其声明为全局变量
- 如果一个变量在函数外没有定义,在函数内部也可以直接将一个变量定义为全局变量,该函数执行后,将增加一个新的全局变量
也可以这么理解:
- 在函数内只引用某个变量的值而没有为其赋新值,如果这样的操作可以执行,那么该变量为(隐式的)全局变量
- 如果在函数内任意位置有为变量赋新值的操作,该变量即被认为是(隐式的)局部变量,除非在函数内显式地用关键字global进行声明
>>> def demo():
... global x #函数内定义x为全局变量
... x=3
... y=4 #y为函数体内的变量(局部变量)
... print(x,y)
...
...
>>> x=5
>>> demo() #调用函数即启动了全局变量x
3 4
>>> x
3
>>> y
Traceback (most recent call last):File "<pyshell#114>", line 1, in <module>y
NameError: name 'y' is not defined
>>> del x
>>> x #全局变量删除后就失效了
Traceback (most recent call last):File "<pyshell#116>", line 1, in <module>x
NameError: name 'x' is not defined
>>> demo() #再次定义了全局变量
3 4
>>> x
3
>>> y
Traceback (most recent call last):File "<pyshell#119>", line 1, in <module>y
NameError: name 'y' is not defined
如果局部变量与全局变量具有相同的名字,那么该局部变量会在自己的作用域内隐藏同名的全局变量。
>>> def demo():
... x=3 #创建了全局变量,并自动隐藏了同名的全局变量
...
...
>>> x=5
>>> x
5
>>> demo()
>>> x #函数执行不影响外面全局变量的值
5
四、lambda表达式
lambda表达式可以用来声明匿名函数,也就是没有函数名字的临时使用的小函数,尤其适合需要一个函数作为另一个函数参数的场合,也可以定义具名函数。
lambda表达式只可以包含一个表达式,该表达式的计算结果可以看作是函数的返回值,不允许包含复合语句,但在表达式中可以调用其他函数。
>>> f=lambda x,y,z:x+y+z #可以给lambda表达式起名字
>>> f(1,2,3) #像函数一样调用
6
>>> g=lambda x,y=2,z=3:x+y+z #参数默认值
>>> g(1)
6
>>> g(2,z=4,y=5) #关键参数
11
>>> L=[1,2,3,4,5]
>>> print(list(map(lambda x:x+10,L))) #模拟向量运算
[11, 12, 13, 14, 15]
>>> L
[1, 2, 3, 4, 5]
>>> data=list(range(20)) #创建列表
>>> data
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
>>> import random
>>> random.shuffle(data) #打乱顺序
>>> data
[16, 2, 15, 0, 7, 17, 12, 14, 9, 11, 4, 18, 3, 8, 1, 10, 19, 13, 6, 5]
>>> data.sort(key=lambda x:len(str(x))) #按转换成字符串以后的长度排序
>>> data
[2, 0, 7, 9, 4, 3, 8, 1, 6, 5, 16, 15, 17, 12, 14, 11, 18, 10, 19, 13]
>>> data.sort(key=lambda x:len(str(x)),reverse=True) #降序排序,字符长度一样保持原位置
>>> data
[16, 15, 17, 12, 14, 11, 18, 10, 19, 13, 2, 0, 7, 9, 4, 3, 8, 1, 6, 5]五、生成器函数设计要点
1.介绍
包含yield语句的函数可以用来创建生成器对象,这样的函数也成生成器函数。
yield语句与return语句的作用类似,都是用来从函数中返回值。与return语句不同的是,return语句一旦执行会立刻结束函数的运行,而每次执行到yield语句并返回一个值后会暂停或挂起后面代码的执行,下次通过生成器对象的__next__()方法、内置函数next()、for循环遍历生成器对象元素或其他方式显式“索要”数据时恢复执行。
生成器具有惰性求值的特点,适合大数据处理。
2.【例5-3】编写并使用能够生成斐波那契数列的生成器函数
>>> def f():
... a,b=1,1 #序列解包,同时为多个元素赋值
... while True:
... yield a #暂停执行,需要时再生产一个新元素
... a,b=b,a+b #序列解包,继续生成新元素
...
...
>>> a=f() #创建生成器对象
>>> for i in range(10): #斐波那契数列前10个元素
... print(a.__next__(),end=' ')
...
...
1 1 2 3 5 8 13 21 34 55
>>> for i in f(): #斐波那契数列中第一个大于100的元素
... if i>100:
... print(i,end=' ')
... break
...
...
144
>>> a=f() #创建生成器对象
>>> next(a) #使用内置函数next()获取生成器对象中的元素
1
>>> next(a) #每次索取新元素时,由yield语句生成
1
>>> a.__next__() #也可以调用生成器对象的__net__()方法
2
>>> a.__next__()
3
>>> next(a)
5