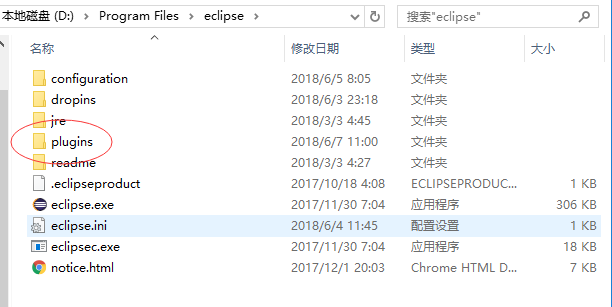
最近，发现新版Eclipse安装的插件不再像以前那样，安装在目录下的plugins的文件夹下，那么，有时候我们自己下载的离线的插件包要放在哪里呢，像往前版本放在目录下的plugins的文件夹下已经不生效了：

那么问题来了，我们在那里找到已经安装的插件包和解压离线的插件放哪里呢？为了解决这个问题，开始我将安装目录的每一个文件都搜了一遍。果然，功夫不负有心人，肯定会隐藏起来，通过配置文件进行关联。

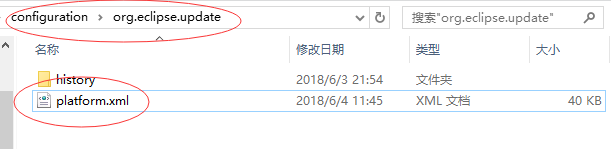
1、找到安装目录的configuration -->> org.eclipse.update (为什么是在这个文件夹里面呢，新版本嘛，所以就在update的配置文件里咯) -->> platform.xml；

2、打开platform.xml文件，看到关键关联代码：url="file:/C:/Users/***/.p2/pool/",原来千呼万唤始出来，隐藏在此处：

3、原来新版安装Eclipse的时候，会在C盘用户文件生成两个关键的配置文件：.eclipse和.p2文件；

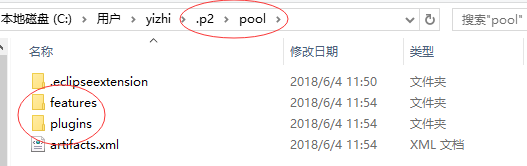
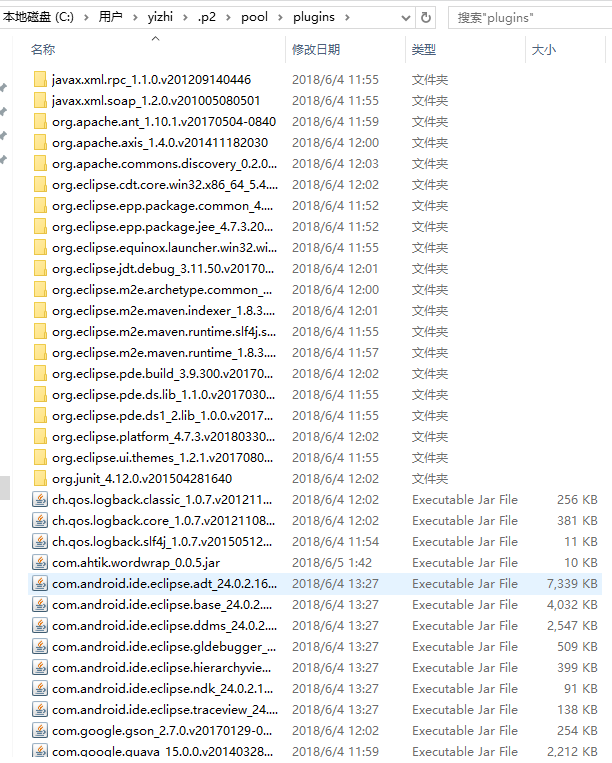
4、打开C盘的.p2文件夹（C:/Users/本机电脑/.p2/pool/）,找到pool,豁然开朗，发现原来插件文件夹features和plugins在此：

5、打开plugins，所有插件尽览无遗：

以后插件就安装在此目录就可以了，完毕。

思考:Eclipse安装以前的方式不是挺好的吗？为什么要这样呢？原因其实很简单，按照以前做法，试想如果我的电脑装了好多个eclipse，都要用到相同的是不是需要装好多次？按照新版本做法，无论安装多少个版本的Eclipse,插件只需安装一次，所有的eclipse都共用一个插件：