1. 容器适配器

1.1 什么是适配器

1.2 STL标准库中stack和queue的底层结构

2. stack和queue的模拟实现

2.1 stack模拟实现

2.2 queue的模拟实现

3. deque的介绍(了解)

3.1 deque的实现原理

3.2 deque的缺陷和使用场景

4. 优先级队列 priority_queue

4.1 priority_queue的介绍

4.2 priority_queue的使用

4.3 priority_queue解决TopK问题

剑指 Offer II 076. 数组中的第 k 大的数字 - 力扣（LeetCode）

215. 数组中的第K个最大元素 - 力扣（LeetCode）

本章完。

1. 容器适配器

1.1 什么是适配器

想了解这里的 "适配器"，我们先去看看电源适配器:

【百度百科】电源适配器又叫外置电源，是小型便携式电子设备及电子电器的供电电压变换设备，常见于手机、液晶显示器和笔记本电脑等小型电子产品上。

电源适配器是进行 "转换" 的，它本质上可以理解为是一个变压器。

标准家庭用电电压为220V，我们设备用电其实并不需要这么高，

而电源适配器可以使较高的交流电压降低到合适于手机电池的直流工作电压。

也就是说，电源适配器是用来 "转换" 的。

再看看容器适配器：

一种用来修饰容器，仿函数或者迭代器的接口的东西。

配接器修改类的接口，使原来不相互匹配的两个类可以相互匹配，进行合作。

1.2 STL标准库中stack和queue的底层结构

前一篇我们提到：虽然stack和queue中也可以存放元素，

但在STL中并没有将其划分在容器的行列，而是将其称为容器适配器，

这是因为stack和队列只是对其他容器的接口进行了包装，

STL中stack和queue默认使用deque，比如：

deque（双端队列，后面讲）（可以手动换成其它的）

2. stack和queue的模拟实现

2.1 stack模拟实现

我们以前已经用C语言写过了一个数组栈：

数据结构与算法⑧(第三章_上)栈的概念和实现(力扣：20. 有效的括号)_GR C的博客-CSDN博客

数组栈和链式栈

实现栈无非就两种结构：数组结构和链式结构，两种结构都可以实现。

数组栈和链式栈哪种结构更好？

相对而言数组的结构实现更优，尾插尾删的效率高，缓存利用率高，它的唯一缺点只是增容，

但是增容1次扩2倍对栈来说本身就比较合理，是无伤大雅的。而链式栈虽然不会空间浪费，

用一个 malloc 申请一个，但是链式栈存在一个致命的缺点：单链表不好出数据，

必须要实现双向链表，否则尾上删除数据将会异常麻烦。

如果硬要使用链式栈：

① 如果用尾做栈顶，尾插尾删，要设计成双向链表，否则删数据效率低。

② 如果用头做栈顶，头插头删，就可以设计成单链表。

在C++我们就可以直接用vector实现数组栈了，体会一下C++的方便，直接放stack.h了：

#pragma once
#include <iostream>
#include <vector>
using namespace std;namespace rtx
{template<class T>class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}T& top(){return _con.back();}const T& top() const{return _con.pop_back();}bool empty() const{return _con.empty();}size_t size() const{return _con.size();}private:vector<T> _con;};
}

测试Test.c:

#include "Stack.h"void test_stack()
{rtx::stack<int> st;st.push(1);st.push(2);st.push(3);st.push(4);st.push(5);cout << "st.size() = " << st.size() << endl;while (!st.empty()){cout << st.top() << " "; // 后进先出st.pop();}cout << endl;
}int main()
{test_stack();return 0;
}

我们这里复用了vector，这是不是适配器呢？

这里并不是，因为底层已经写死了，它就是数组栈，如果我想要一个链式栈呢？

模板的方便又来了：

#pragma once
#include <iostream>
#include <vector>
using namespace std;namespace rtx
{template<class T, class Container>class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}T& top(){return _con.back();}const T& top() const{return _con.pop_back();}bool empty() const{return _con.empty();}size_t size() const{return _con.size();}private://vector<T> _con;Container _con;};
}

#include "Stack.h"void test_stack()
{rtx::stack<int, vector<int>> st;st.push(1);st.push(2);st.push(3);st.push(4);st.push(5);cout << "st.size() = " << st.size() << endl;while (!st.empty()){cout << st.top() << " "; // 后进先出st.pop();}cout << endl;
}int main()
{test_stack();return 0;
}

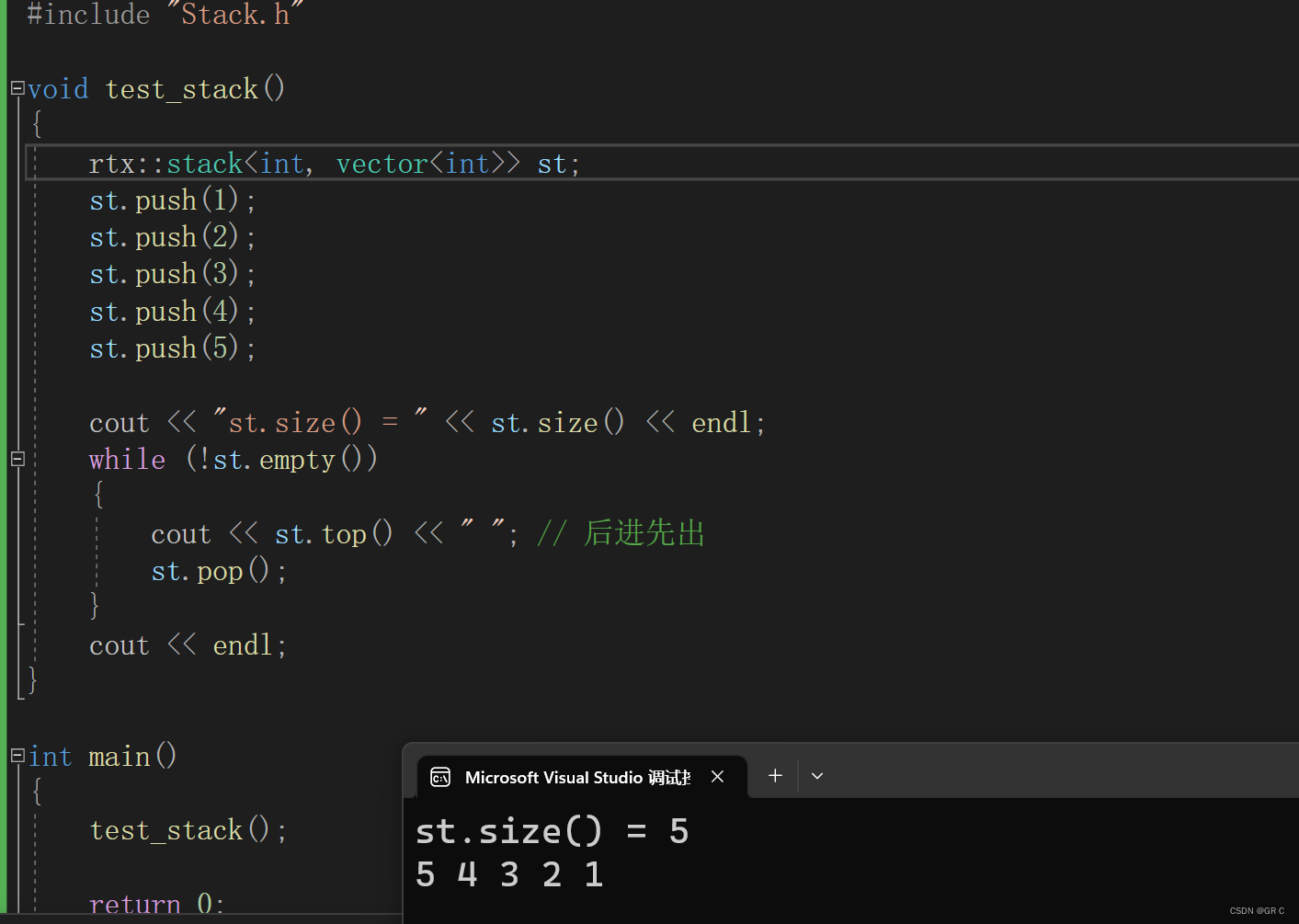
如果我们要链式栈：把显示传的vector换成list（包一下头文件）：

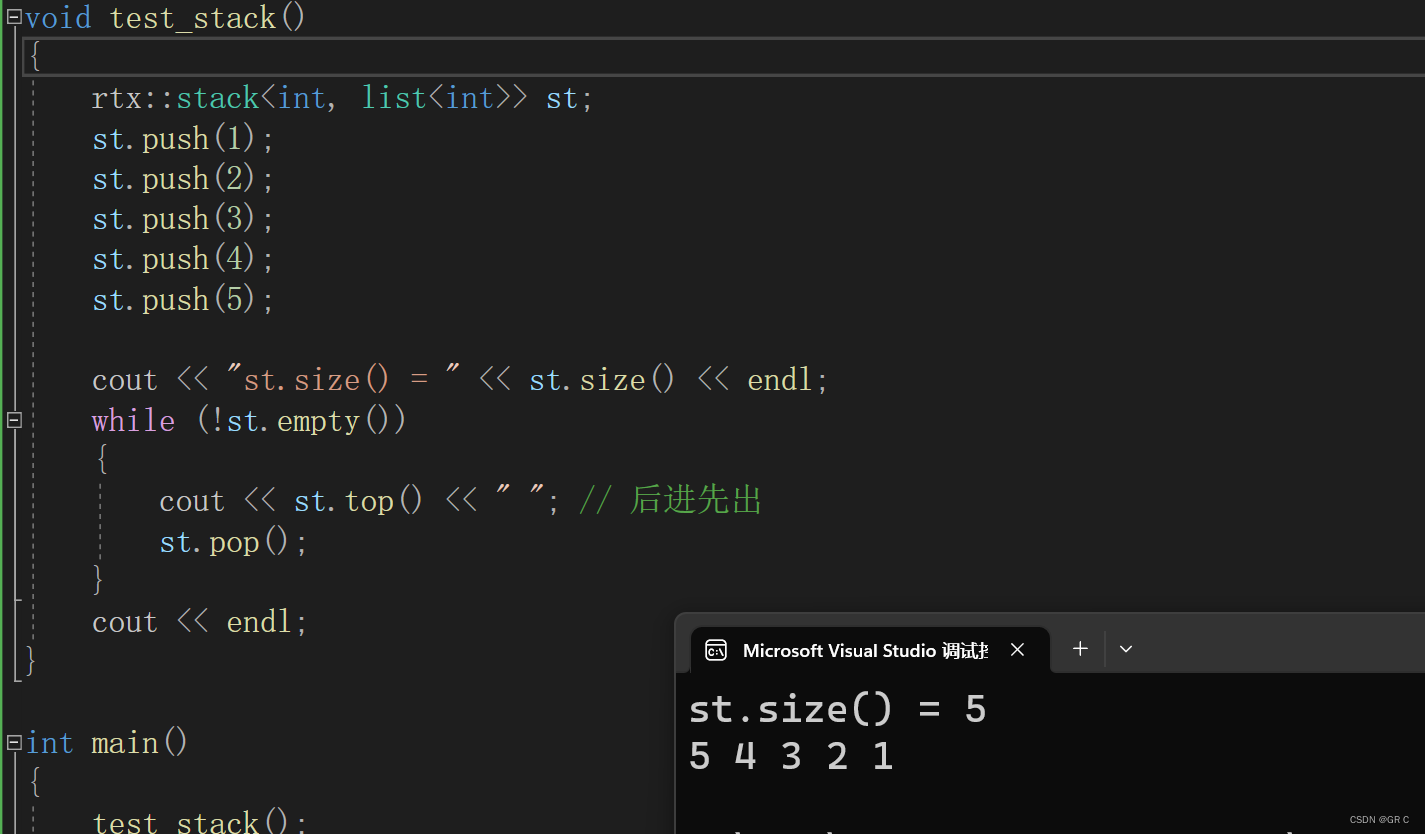
前面说到，STL里面stack和queue的默认适配器是deque：

把其它头文件移到Test.c ，Stack.h的最终就是这样的：

#pragma once#include <deque>namespace rtx
{template<class T, class Container = deque<T>>class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}T& top(){return _con.back();}const T& top() const{return _con.pop_back();}bool empty() const{return _con.empty();}size_t size() const{return _con.size();}private:Container _con;};
}

2.2 queue的模拟实现

deque等下讲，这里先放queue的模拟实现，经过前面的学习，直接放了:

Queue.h:

#pragma once#include <deque>namespace rtx
{template<class T, class Container = deque<T>>class queue{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_front();}T& back(){return _con.back();}T& front(){return _con.front();}const T& back() const{return _con.back();}const T& front() const{return _con.front();}bool empty()  const{return _con.empty();}size_t size() const{return _con.size();}private:Container _con;};
}

Test.c:

#include <iostream>
#include <vector>
#include <list>
#include <string>
using namespace std;#include "Stack.h"
#include "Queue.h"void test_stack()
{rtx::stack<int> st;st.push(1);st.push(2);st.push(3);st.push(4);st.push(5);cout << "st.size() = " << st.size() << endl;while (!st.empty()){cout << st.top() << " "; // 后进先出st.pop();}cout << endl;
}
void test_queue()
{rtx::queue<int> q;q.push(1);q.push(2);q.push(3);q.push(4);q.push(5);cout << "q.size() = " << q.size() << endl;while (!q.empty()){cout << q.front() << " "; // 先进先出q.pop();}cout << endl;
}
int main()
{test_stack();test_queue();return 0;
}

值得注意的是这里的queue不能显示地传vector，因为vector没有头删。

3. deque的介绍(了解)

deque ：双端队列 - double ended queue

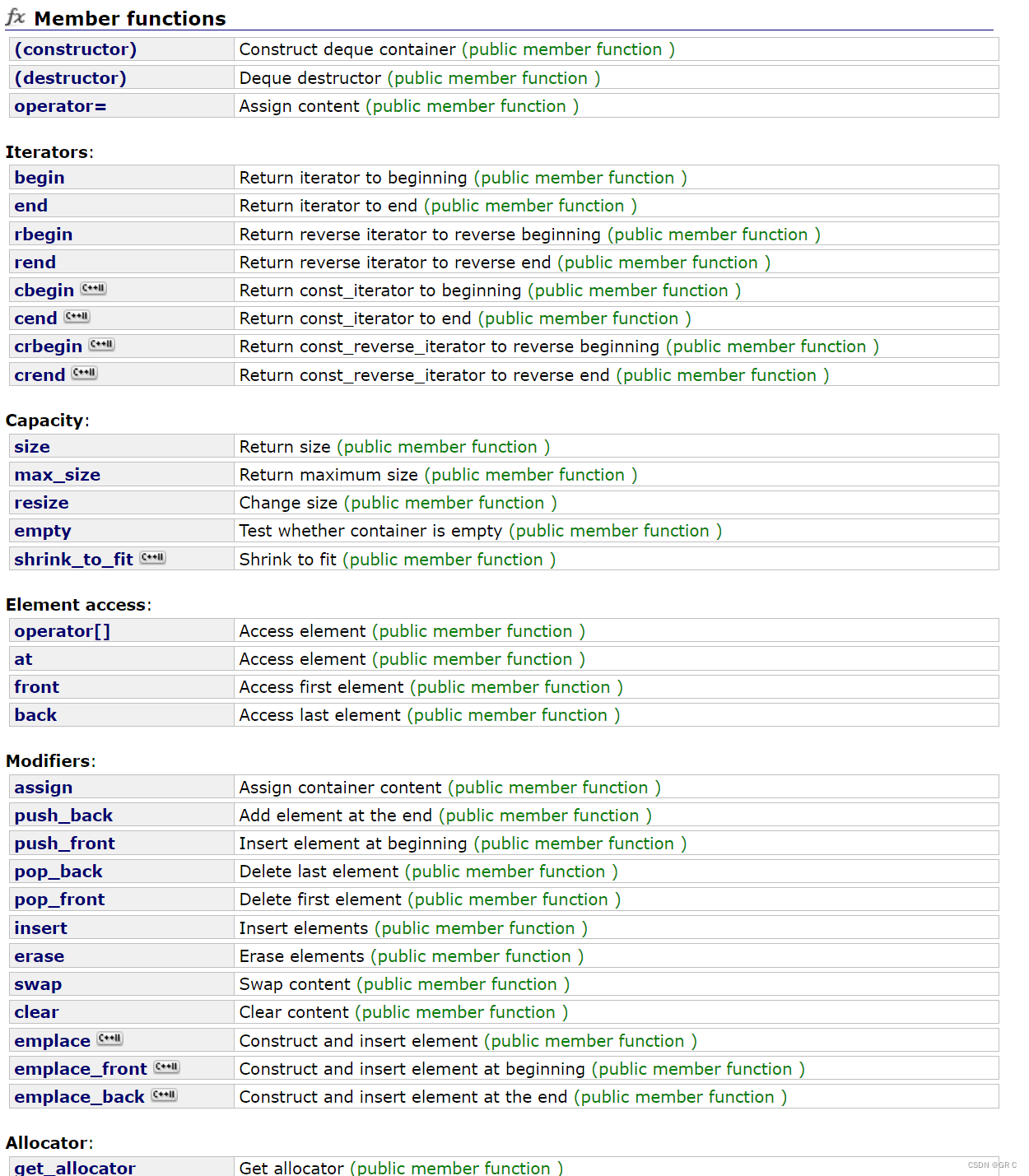
可以发现它的接口很多，有[ ] 也有头删。

deque 是一种双开口的 "连续" 空间的数据结构，

deque 可以在头尾两端进行插入和删除操作。且时间复杂度为O（1），

与 vector 相比，头插效率高，不需要搬移元素，与 list 相比，deque 的空间利用率更高。

3.1 deque的实现原理

deque 并不是真正连续的空间，而是由一段段连续的小空间拼接而成的。

实际的 deque 类似于一个动态的二维数组，其底层结构如下所示：

双端队列底层是一个假想的连续空间，实际是分段连续的，

为了维护其 "整体连续" 、以及随机访问的假象，其重任落在了 deque 的迭代器身上。

因此 deque 的迭代器设计就尤为复杂，如下图所示：

那 deque 是如何借助其他迭代器维护其假想连续的结构的呢？

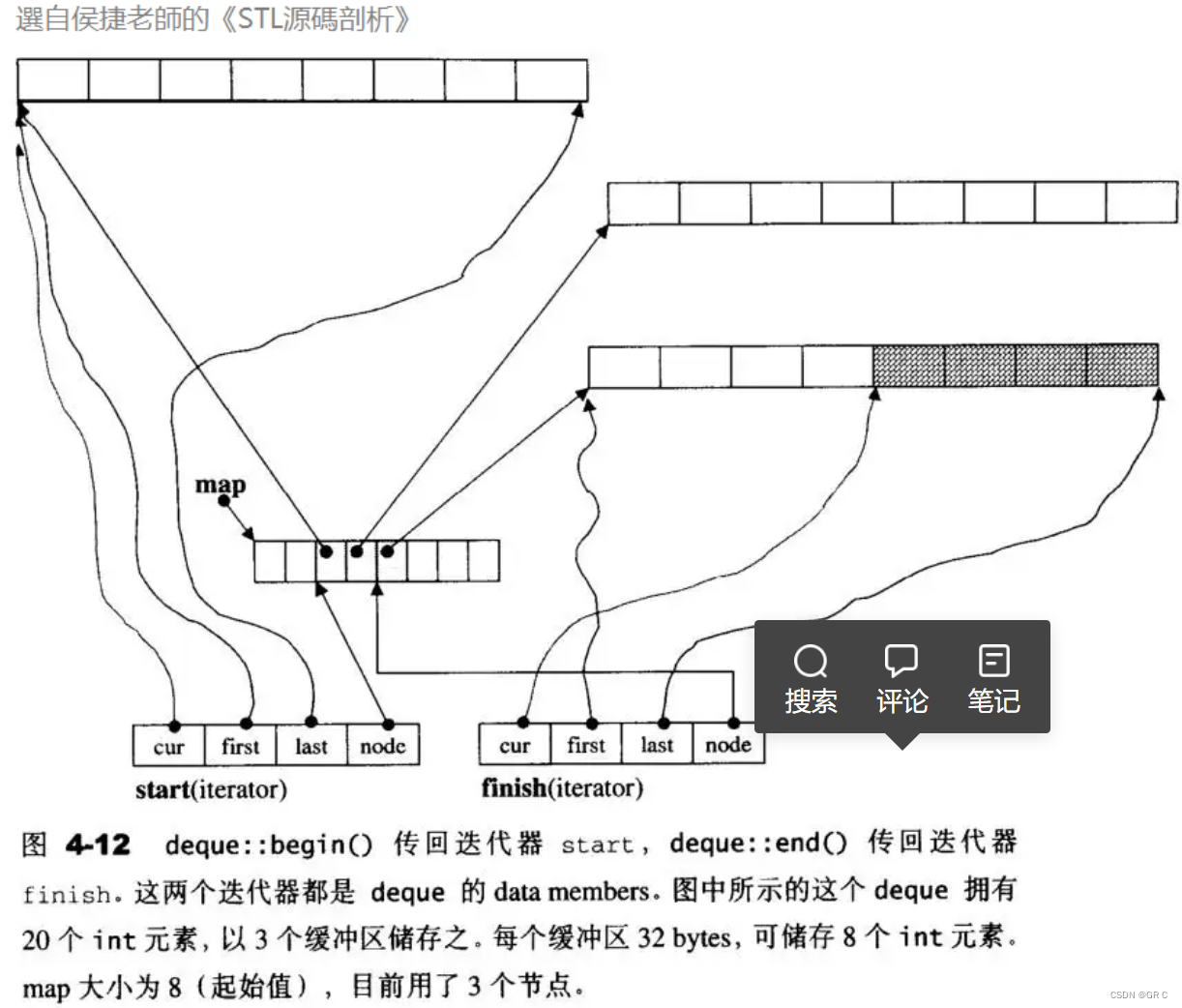
3.2 deque的缺陷和使用场景

deque 有点像 vector 和 list ，我们把 vector 和 list 也拉出来进行优缺点的对比再合适不过了：

那什么场景适合用 deque 呢？

虽然不够极致但是还是有用武之地的：大量头尾插入删除，偶尔随机访问的情况可以使用 deque。

前面说到：在 stack 和 queue 的实现上，是选择 deque 作为底层默认容器的。

为什么选择 deque 作为 stack 和 queue 的底层默认容器？

① stack 是一种后进先出的特殊线性数据结构，因此只要具有 push_back() 和 pop_back() 操作的线性结构，都可以作为 stack 的底层容器，比如 vector 和 list 都可以。

② queue 是先进先出的特殊线性数据结构，只要具有 push_back() 和 pop_front() 操作的线性结构，都可以作为 queue 的底层容器，比如 list 。

但 STL 最终选择用 deque 作为 stack 和 queue 的底层容器，其主要原因是如下：

stack 和 queue 不需要遍历（因此 stack 和 queue 没有迭代器），

只需要在固定的一端或者两端进行操作。
在 stack 中元素增长时，deque 比 vector 的效率高（扩容时不需要搬移大量数据）；

queue 中的元素增长时，deque 不仅效率高，而且内存使用率高。

结合了 deque 的优点，而完美的避开了其缺陷。

4. 优先级队列 priority_queue

4.1 priority_queue的介绍

priority_queue的底层就是以前数据结构学的堆：

数据结构与算法⑪(第四章_中)堆的分步构建_GR C的博客-CSDN博客

https://cplusplus.com/reference/queue/priority_queue/

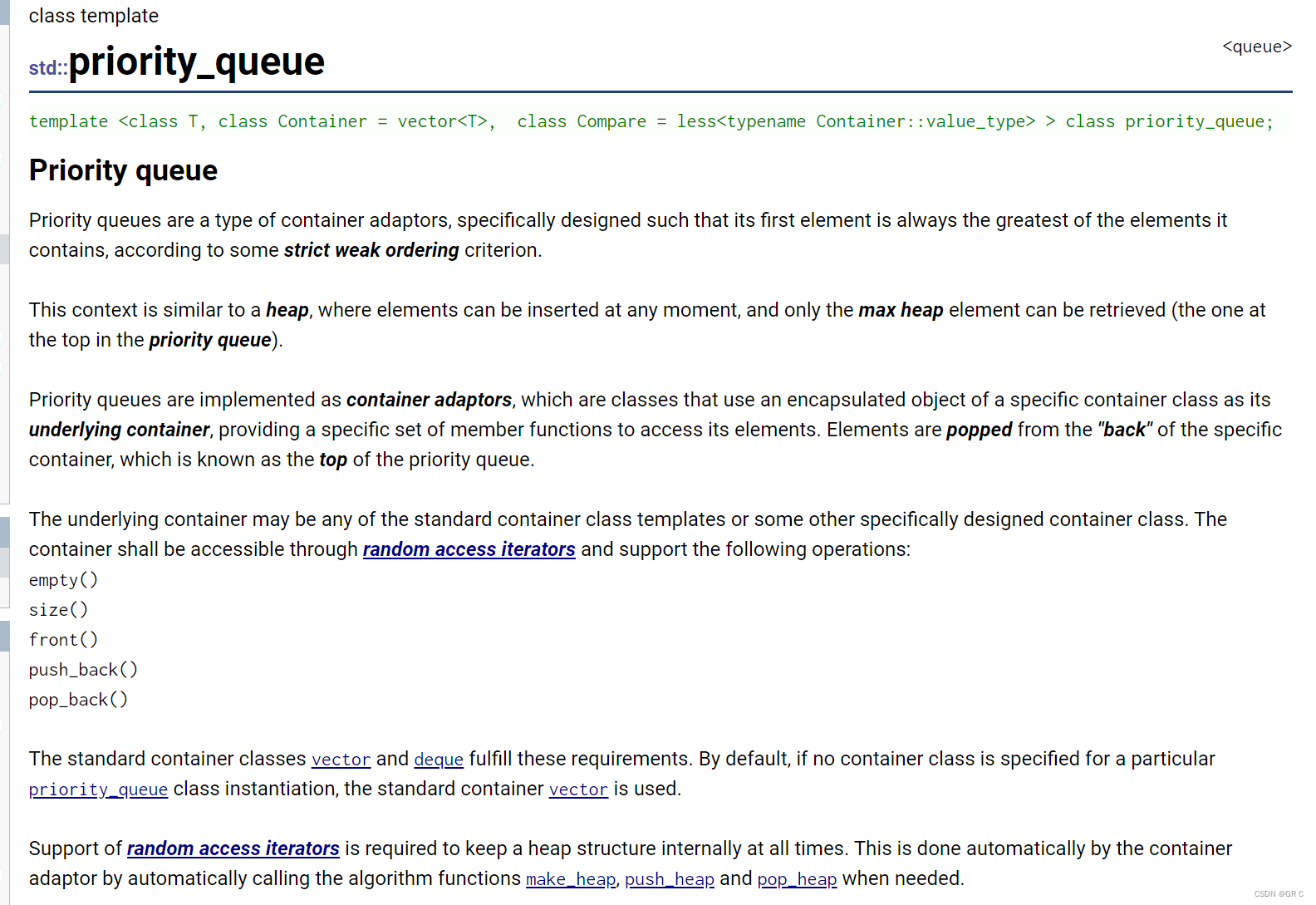
优先队列是一种容器适配器，根据严格的弱排序标准，

它的第一个元素总是它所包含的元素中最大的。
此上下文类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素

（优先队列中位于顶部的元素）。
优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，

queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出，

其称为优先队列的顶部。
标准容器类 vector 和 deque 满足这些需求。默认情况下，

如果没有为特定的 priority_queue 类实例化指定容器类，则使用 vector。
需要支持随机访问迭代器，以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数 make_heap、push_heap 和 pop_heap 来自动完成此操作。
底层容器可以是任何标准容器类模板，也可以是其他特定设计的容器类。

容器应该可以通过随机访问迭代器访问，并支持以下操作：

empty()：检测容器是否为空
size()：返回容器中有效元素个数
front()：返回容器中第一个元素的引用
push_back()：在容器尾部插入元素
pop_back()：删除容器尾部元素

4.2 priority_queue的使用

优先级队列默认使用 vector 作为其底层存储数据的容器，

在 vector 上又使用了堆算法将 vector 中元素构造成堆的结构，因为 priority_queue 就是堆。

所有需要用到堆的地方，都可以考虑使用 priority_queue。

值得注意的是，priority_queue 默认为大根堆。注意下面是反过来的：

优先级队列默认大的优先级高，传的是 less 仿函数，底层是一个大堆；

如果想控制小的优先级高，需手动传 greater 仿函数，其底层是一个小堆。

（仿函数后面讲，实现优先级队列时详细讲解，现在只需要知道如何使用即可）

看看文档使用：

常用接口函数：

代码使用：（包的是queue的头文件）

#include <iostream>
#include <queue>
using namespace std;void test_priority_queue()
{priority_queue<int> pq;//默认大堆优先级高pq.push(3);pq.push(1);pq.push(2);pq.push(5);pq.push(0);pq.push(8);pq.push(1);while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;// 迭代器区间初始化：原生指针也是迭代器int arr[] = { 3, 2, 7, 6, 0, 4, 5, 9, 8, 1 };priority_queue<int> heap(arr, arr+sizeof(arr)/sizeof(arr[0]));while (!heap.empty()){cout << heap.top() << " ";heap.pop();}cout << endl;
}
int main()
{//test_stack();//test_queue();test_priority_queue();return 0;
}

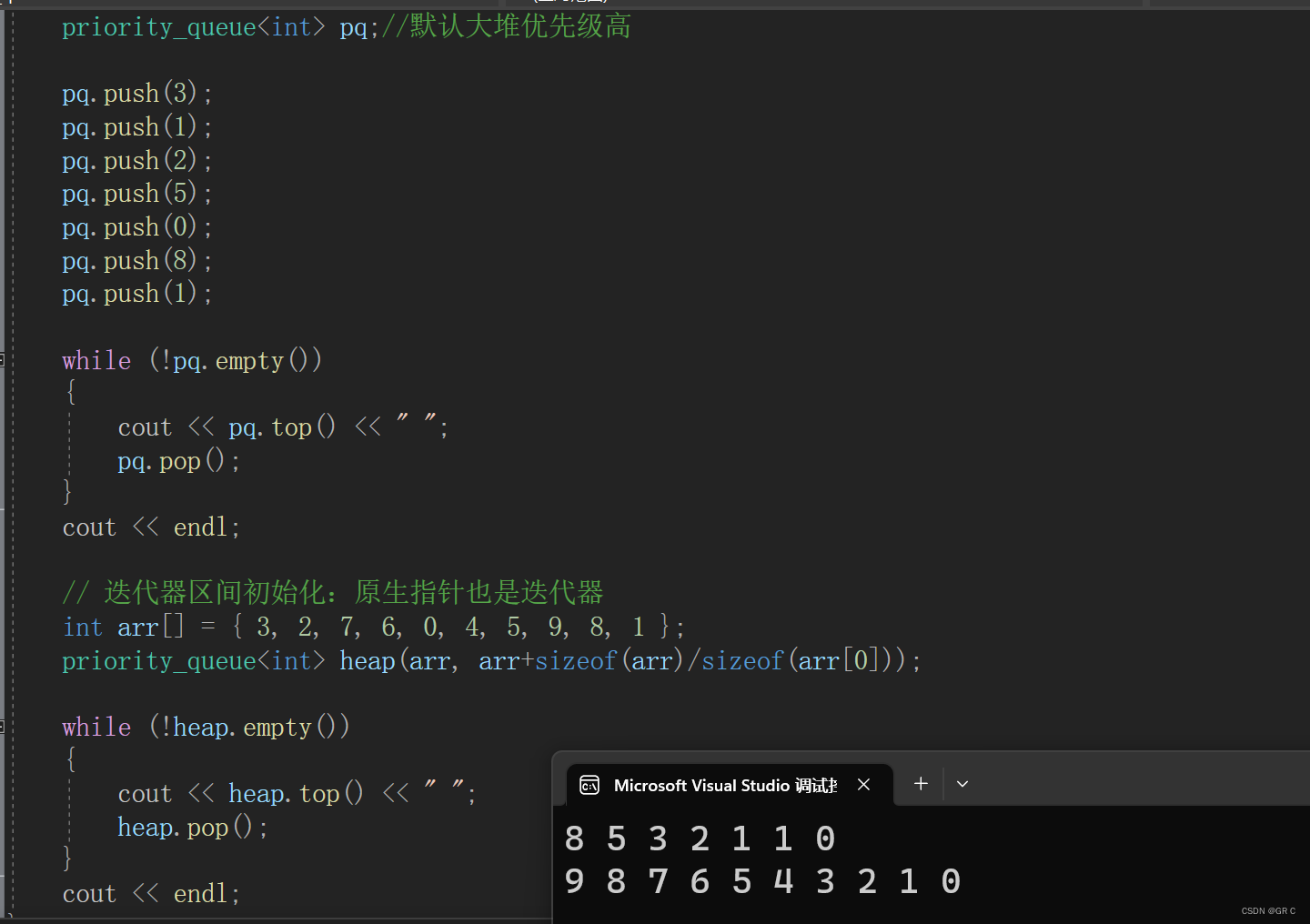
默认是用 vector 存储的，注意这里没有明确指定 less 还是 greater，所以默认为 less。

令该优先级队列以小的优先级高：在定义优先级队列时主动去传 greater<int>

（包一下头文件functional）因为传 greater<int> 是在第三个参数接收的，

如果你想传第三个模板参数，你必须得先传第二个（下面是定义，仔细观察缺省值部分）

代码演示小的优先级高：

#include <iostream>
#include <queue>
#include <vector> 
#include <functional> // greater和less的头文件
using namespace std;void test_priority_queue()
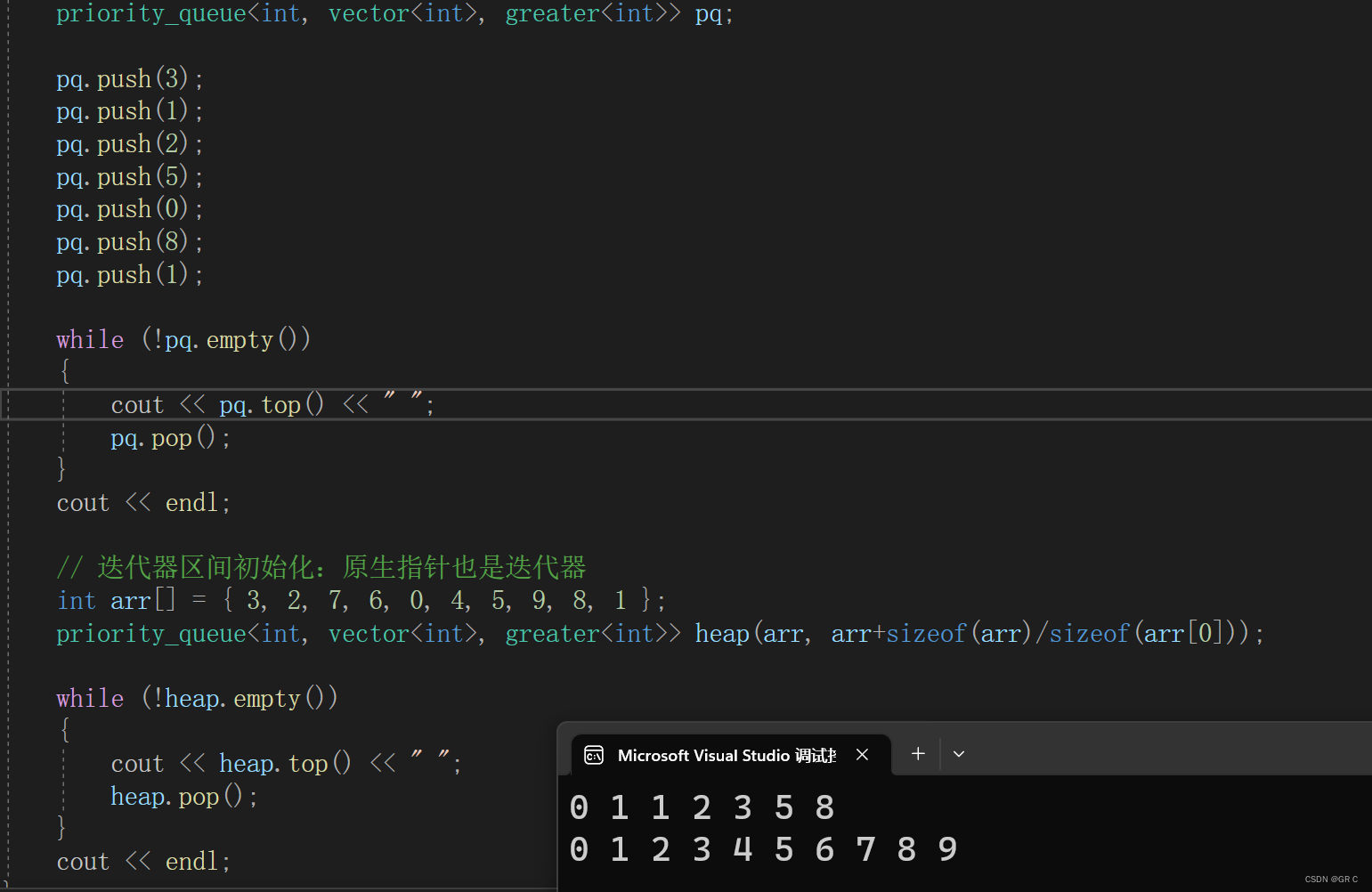
{priority_queue<int, vector<int>, greater<int>> pq;pq.push(3);pq.push(1);pq.push(2);pq.push(5);pq.push(0);pq.push(8);pq.push(1);while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;// 迭代器区间初始化：原生指针也是迭代器int arr[] = { 3, 2, 7, 6, 0, 4, 5, 9, 8, 1 };priority_queue<int, vector<int>, greater<int>> heap(arr, arr+sizeof(arr)/sizeof(arr[0]));while (!heap.empty()){cout << heap.top() << " ";heap.pop();}cout << endl;
}
int main()
{//test_stack();//test_queue();test_priority_queue();return 0;
}

值得注意的是如果在priority_queue中放自定义类型的数据，

用户需要在自定义类型中提供> 或者< 的重载。（像日期类一样）

4.3 priority_queue解决TopK问题

剑指 Offer II 076. 数组中的第 k 大的数字 - 力扣（LeetCode）

215. 数组中的第K个最大元素 - 力扣（LeetCode）

（这两题是一样的，我们在讲TopK问题的时候也用C语言写过：）

数据结构与算法⑬(第四章_中_续二)堆解决Topk问题+堆的概念选择题_GR C的博客-CSDN博客

难度中等

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入:

[3,2,1,5,6,4],

k = 2
输出: 5

示例 2:

输入:

[3,2,3,1,2,4,5,5,6],

k = 4
输出: 4

提示：

1 <= k <= nums.length <= 10^5

-10^4 <= nums[i] <= 10^4

int findKthLargest(int* nums, int numsSize, int k){}

解析代码：（sort一下也能过，但是时间是O（N*logN））

和以前一样：这里我们需要把整个数组建成一个大堆，然后pop（k-1）次堆顶的元素后堆顶的元素

就是第k大的数。而且我们不用自己写大堆下调算法了，建堆也可以直接用priority_queue:

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {//把整个数组建成一个大堆，(O(N))priority_queue<int> MaxHeap(nums.begin(),nums.end());while(--k)//然后pop（k-1）次堆顶的元素(log(N*K)){MaxHeap.pop();}return MaxHeap.top();//堆顶的元素就是第k大的数}
};

看下C语言写的：（调整算法后面模拟实现priority_queue还会用，面试可能也要写）

void Swap(int* px, int* py)
{int tmp = *px;*px = *py;*py = tmp;
}void justDown(int* arr, int n, int root)//大堆下调
{int father = root;int child = father * 2 + 1;//默认左孩子大while (child < n){if (child + 1 < n && arr[child] < arr[child + 1]){  // 如果右孩子存在且右孩子比左孩子大child++;}if (arr[father] < arr[child]){Swap(&arr[father], &arr[child]);father = child;child = father * 2 + 1;}else{break;}}
}int findKthLargest(int* nums, int numsSize, int k) {for (int i = (numsSize - 1 - 1) / 2;i >= 0;i--) //建堆的for写法{justDown(nums, numsSize, i);}// 删除数据for (int i = 1;i <= k - 1;i++){Swap(&nums[0], &nums[numsSize - i]);justDown(nums, numsSize - i, 0);//删除多少个numsize-多少个}return nums[0];
}