一、重心坐标，插值

上篇的最后我们提到了，当顶点在纹理上的对应uv坐标成功找到之后，三角形三个顶点中间的值需要用三角形的重心坐标插值计算得到，那么这个运算是怎么进行的，本篇我们将介绍。插值的运算不仅仅在纹理中，包括三角形内部的颜色和法线都可以用插值来计算并由此得到一个平滑的过度。

那么什么是重心坐标？首先我们明确重心坐标是定义在三角形上的一个坐标系，而不同的三角形有不同的重心坐标。重心坐标告诉我们，三角形内任意一点的坐标都可以由三个顶点的坐标的线性组合来表示，只要满足线性组合系数之和(α+β+γ)为1并且α,β,γ>0，如上图。（如果不满足α,β,γ>0，那么只能确定该点在三角形所在平面内，至于是三角形内外并不能确定）

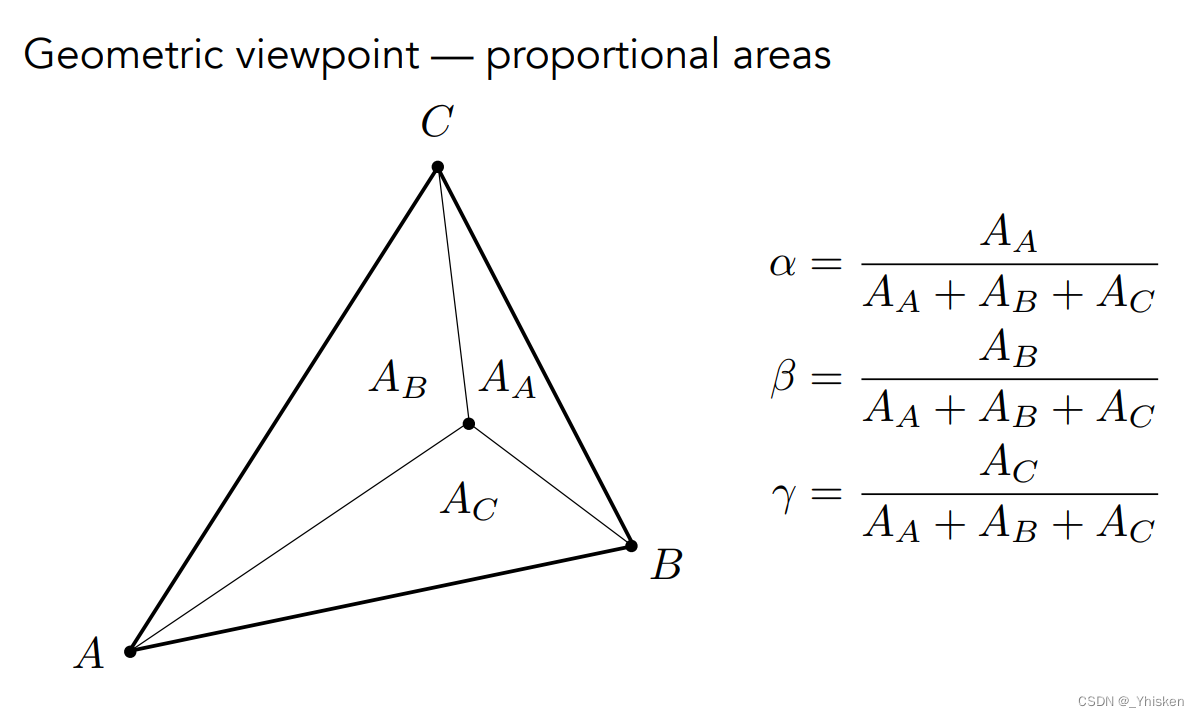
重心坐标的表示就是(α,β,γ),如A点的重心坐标就是(1,0,0)。那么如何确定任意一点的重心坐标呢？这里要通过面积比来算，如上图中一点的坐标，α,β,γ各个值就是另两个顶点连成的三角形在总面积的占比，如上图所示。

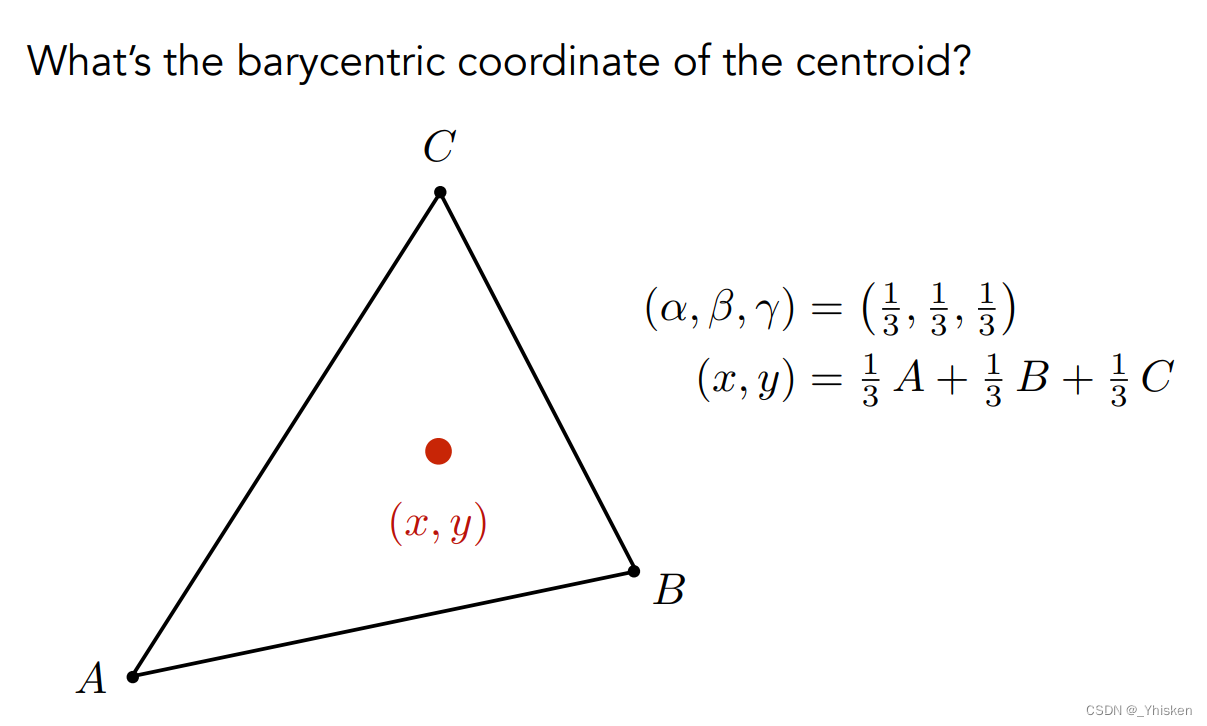
而通过如上的表示，我们马上可以找到一个及其特殊的点，就是三角形自己的重心，它的重心坐标是(1/3,1/3,1/3)，这个点与三个顶点连线分成的三个三角形面积也恰好相等。

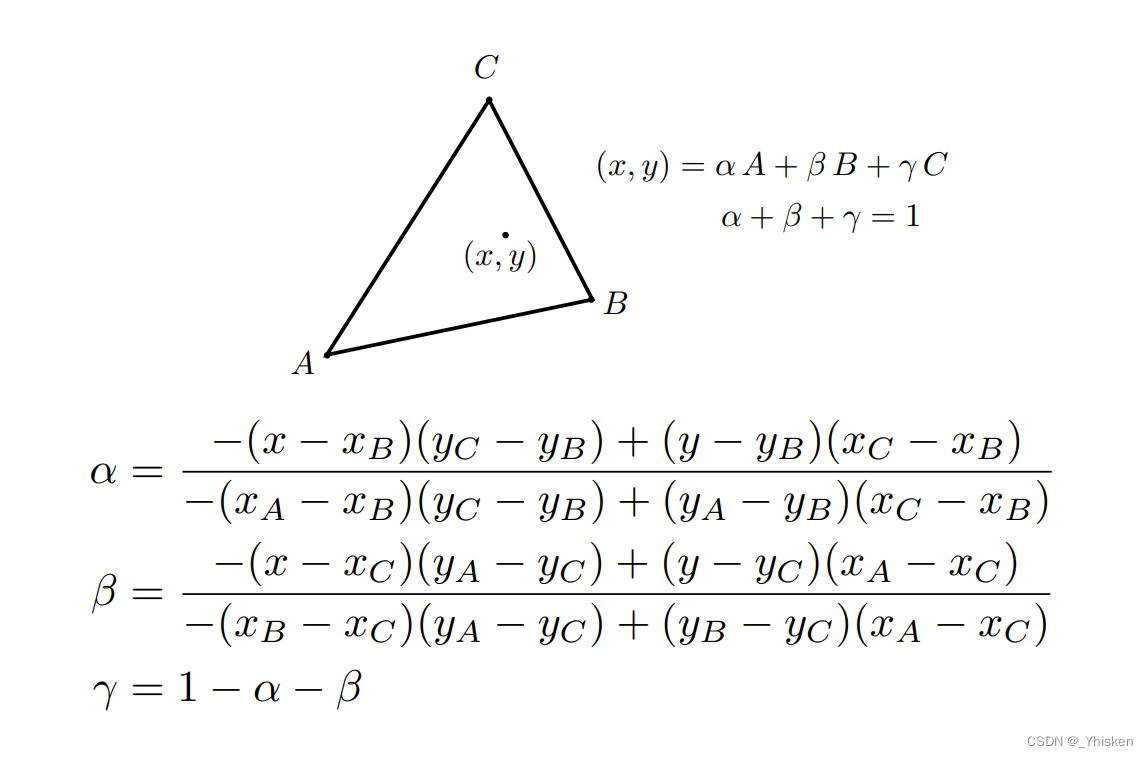
上图为对于三角形内任意一点的重心坐标计算的通用表达式

通过以上的介绍，我们知道了三角形内部的任意一点的坐标可以通过重心坐标求出表示出来，那么我们也可以利用重心坐标求三角形内部任意一点的其它属性，其他三角形内部的属性也可以用重心坐标的线性组合表示出来，如上图的颜色插值。（注意：重心坐标并没有投影下不变的性质，所以在插值如深度这种空间中的性质时，应该先在3D空间中用三维的坐标算出三维空间中的重心坐标进行插值，然后再放回而不能直接在投影之后的三角形中做插值。至于如何在已经投影的三角形在回到三维空间，应用逆变换即可。）

二、应用纹理

1.纹理的放大

在应用纹理的过程中，如果纹理过小，会导致问题。这借化用闫令琪老师在GAMES101中举的例子，假设有一个4K分辨率的墙，但是贴上去的纹理只有256x256，那么当在查询纹理的时候，就会查到许多非整数，也就说纹理会被拉大，也就会形成下图所示的样子。

在第一幅图中(Nearest)，我们采用了简单的四舍五入，即如果映射到非整数，则四舍五入取整，这会导致问题，许多像素会被映射到同一个纹素(texel)上，如第一幅图中的锯齿/方块化

(1)双线性插值

如上所示的四舍五入达到的效果显然是不美观的，于是我们找到了其他方案：Bilinear interpolation，中文名双线性插值。

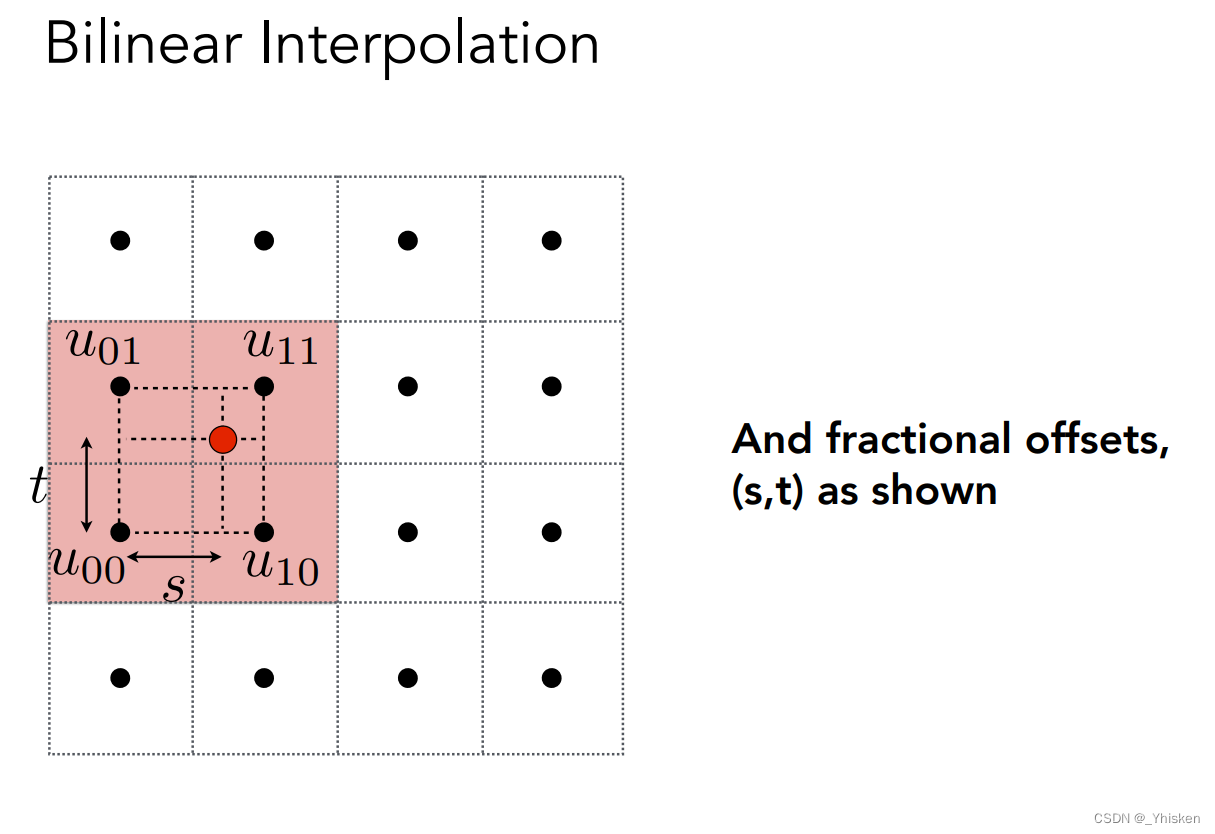
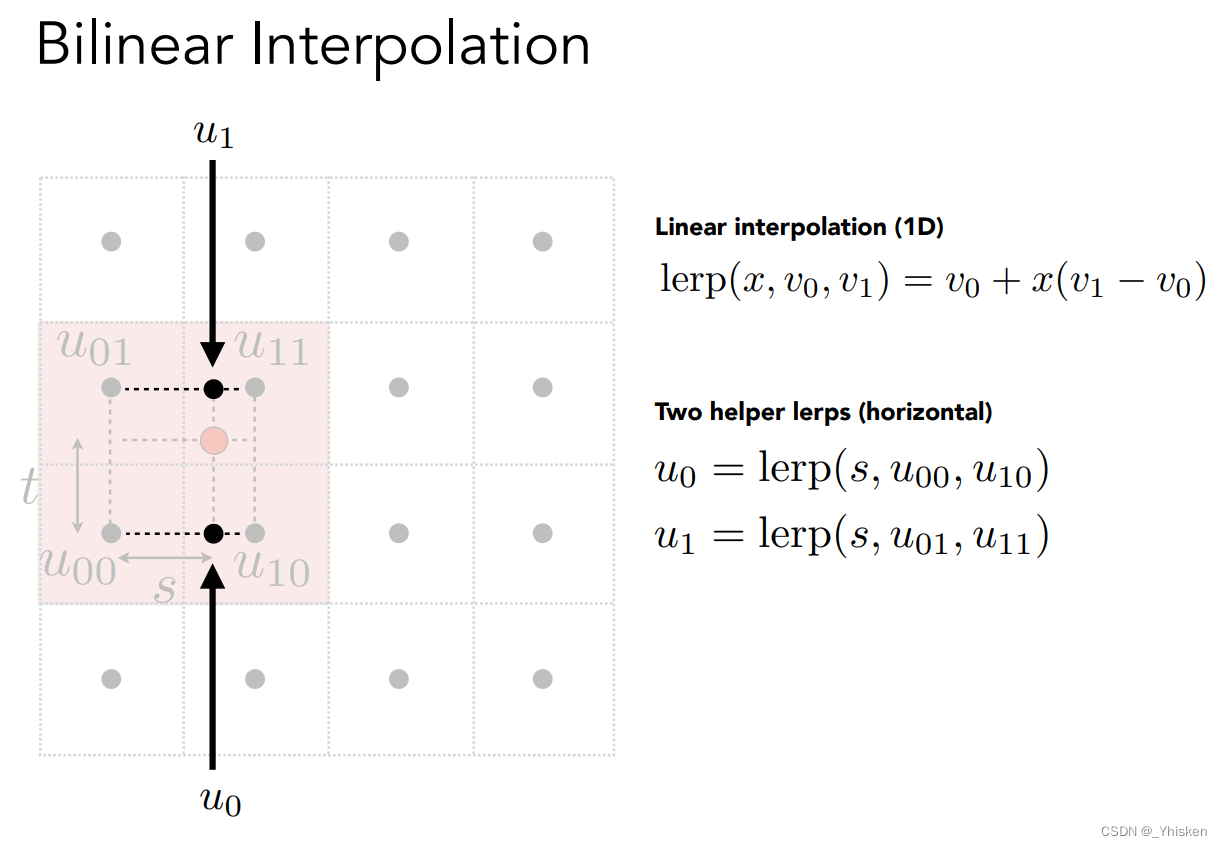
假设我们的某一个在高分辨率下的像素(上图的红点)映射到了比较小的一块纹理(上图的4X4区域)上，那么我们取临近这个点最近的四个纹素，从左下角的纹素的中心开始，计算它水平和竖直方向的距离，分别为s，t。接着我们定义一步插值(lerp)操作。(什么是插值：假如两点分别为0和1，那么中间即为0.5，0-0.5中间为0.25，其它同理来得出0-1中每个点的值，这种通过两点属性确定中间任何一点属性的办法叫做插值运算。公式如上图)。

通过插值运算，我们可以得出如上图中u01、u11之间和u00、u10之间的对应纹理颜色，也就是点u1和u0对应颜色，而再把u1和u0之间做一次插值运算，就可以得到红点对应纹理的颜色了。而如上的方法就叫做双线性插值。得到的下面第二幅图明显优于第一幅简单四舍五入得到的图。

(2)立方卷积插值

而第三幅图Bicubic，中文名立方卷积插值/双三次插值，则是取周围16个点进行插值的运算，达到的效果会更好。

(鄙人补充：在GAMES101中闫令琪老师没有提到的插值—兰索斯插值Lanczos，是取周围64个点做插值，但性能消耗很大，所以没有得到广泛应用，关于Bicubic和Lanczos，GAMES101中并没有详细介绍，但是思想和Bilinear几乎相同，只是参考样板变多了，感兴趣的朋友可以自行了解。)

2.纹理的缩小

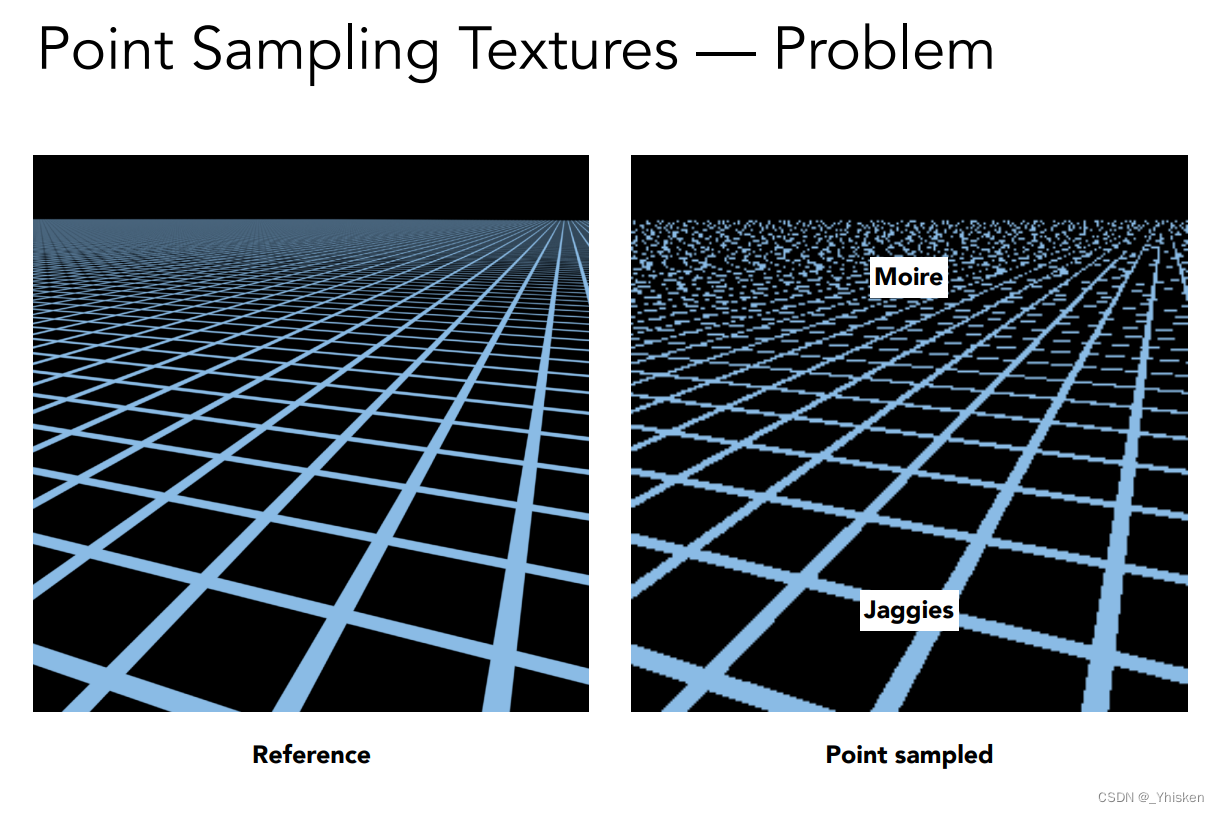
纹理过小会导致问题，同样的纹理过大同样会导致严重的问题，如上图，远处的摩尔纹和近处的锯齿，也就是走样。

(1)哪里出了问题

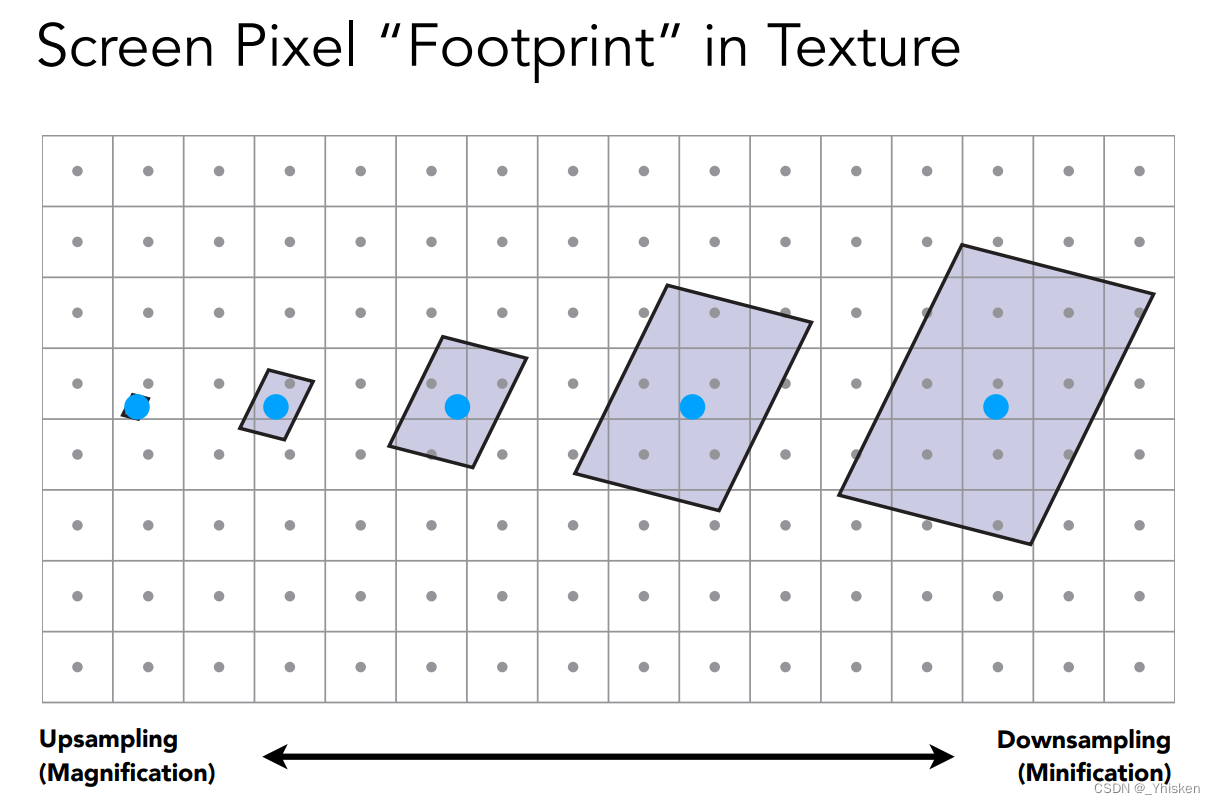
我们知道，我们最终在屏幕上绘制的图像是透视投影，也就是近大远小，那么相同大小的像素在屏幕上对近处和远处的物体覆盖面积是不同的，那么这个时候如果还是只用像素映射的纹素中心来当成映射到的纹理，显然是不正确的，如上图中最右边的区域，如此大的覆盖区域，颜色却只用一个被映射至中心的纹素表示，显然这是不合理的。

那么我们能否用前几篇中的超采样来解决这个走样问题呢？答案是可以。[计算机图形学]反走样(前瞻预习/复习回顾)__Yhisken的博客-CSDN博客

上图所示的就是每个像素用512个采样点来获取对应的纹理上纹素的颜色做加权平均得出的结果。但是显然我们不希望这么做，这会大大提升性能的消耗。

(2)从信号角度分析

前面我们讲到过，走样是由于我们的信号变化过快，而采样的频率跟不上信号变化速度所导致的。在这里的体现就是，我们的一个像素覆盖了纹理上的很大一块区域，也就是说像素内部的纹理信号变化的非常快，但是我们只用了一个像素去采样，也就是说采样的频率明显跟不上信号变化的速度。上面提到的超采样就是我们试图加快采样的频率所得出的办法，但显然不够经济。

(3)Mipmap

我们想，如果我们不进行采样，而是给定一块区域我们马上就能得到它的平均值，那不是好很多吗？确实，而这属于范围查询问题，我们上面说的在很小一块纹理上得出值的问题是点查询，而在大纹理的范围中查询平均值属于范围查询问题(范围查询隶属算法问题，不仅仅是求平均值，还有求最大值最小值等。)

而这就要提到我们的Mipmap，它允许我们做快速的范围查询，速度很快，但只是做近似，所以实际结果并不是百分百的准确，同时，他只能做正方形的范围查询。

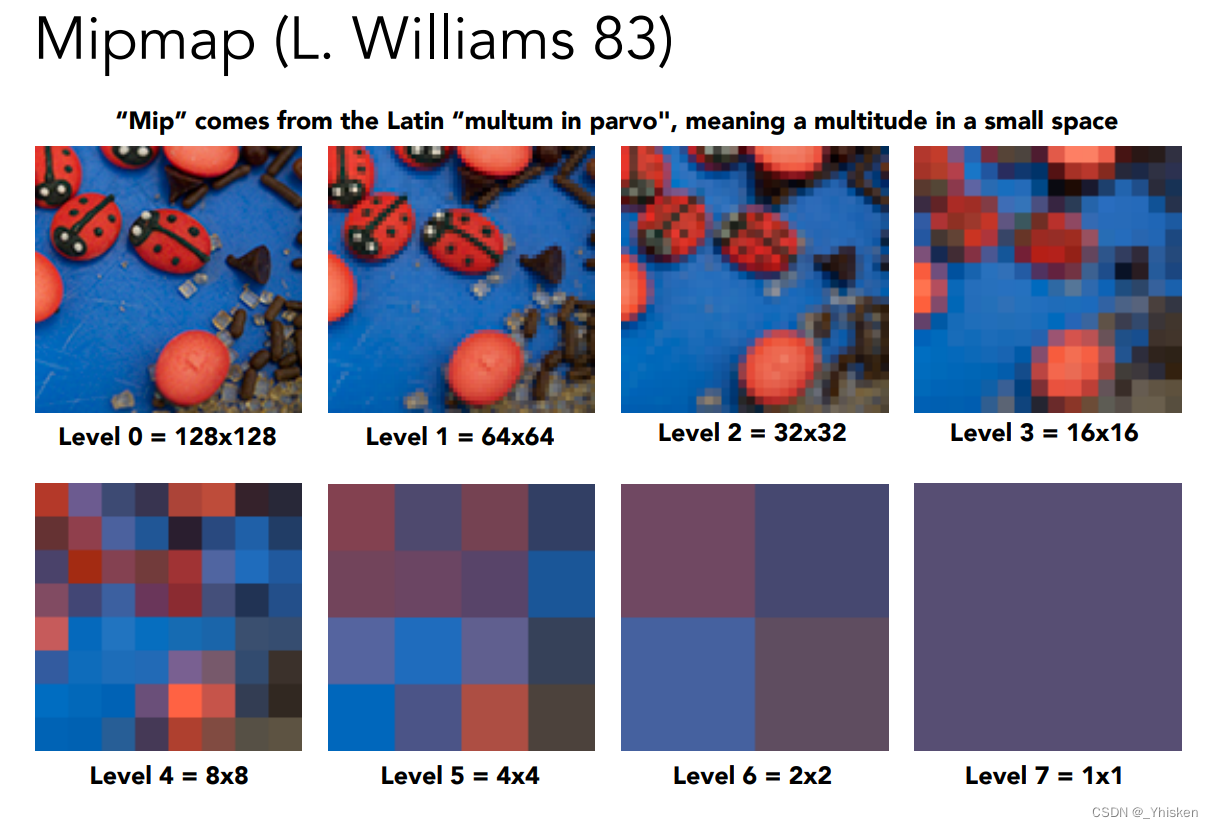
Mipmap如上图所示，就是从第一张图(128x128)生成一系列图的过程，而每下一层大小都是上一层的1/4，分辨率缩小一半。一共就会生成log2分辨率层，图中则为7层。

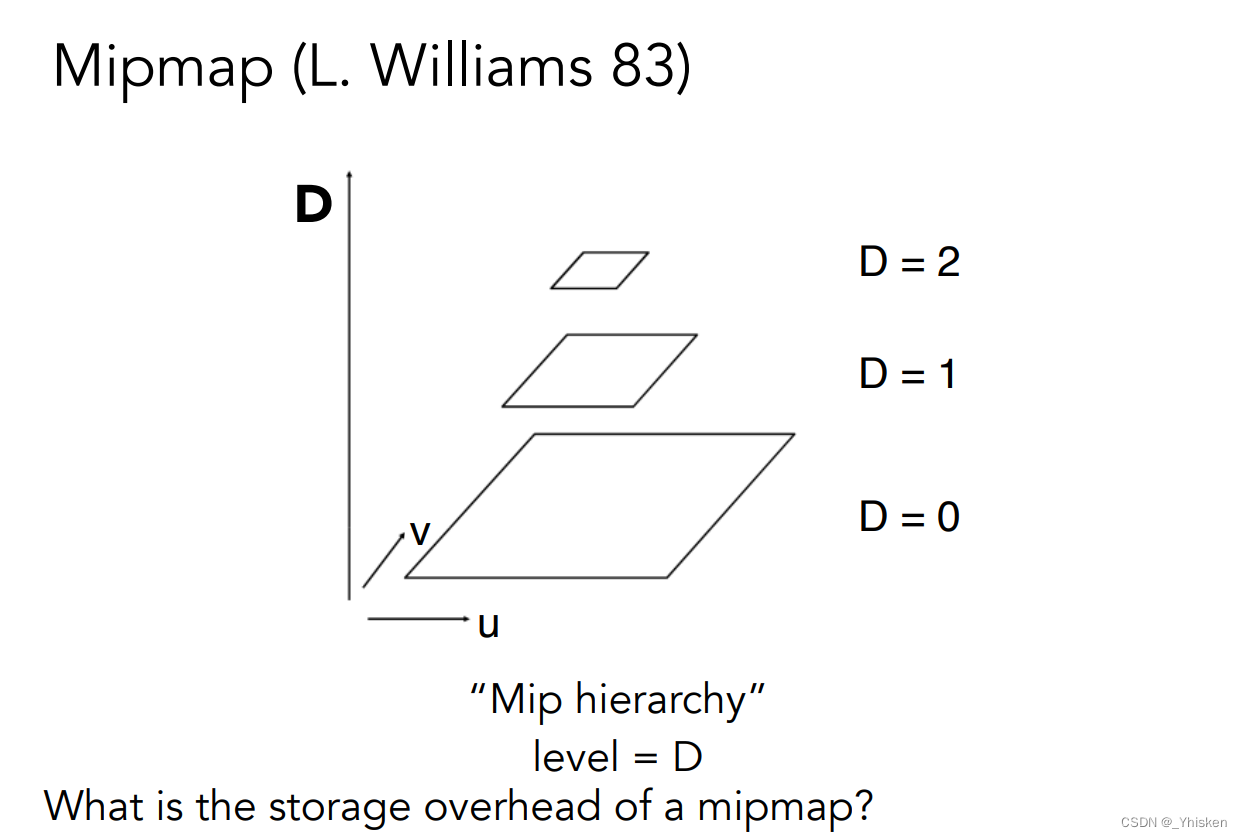
而通过Mipmap，在我们每次渲染之前都把纹理缩小的一系列图储存起来，渲染时直接拿来用，这就可以大大提高我们的便利。而根据我们上面所说，每一张缩小图都是上一张图的1/4，所以即使是无限多张缩小图，我们的储存空间通过求极值可知，也只比原来多了1/3，也就是从1变成了4/3。由此可以看出Mipmap是一种很经济的做法。

那么如何确定我们查询的范围有多大呢？也就是说我们每个像素覆盖纹理的区域如何得到？

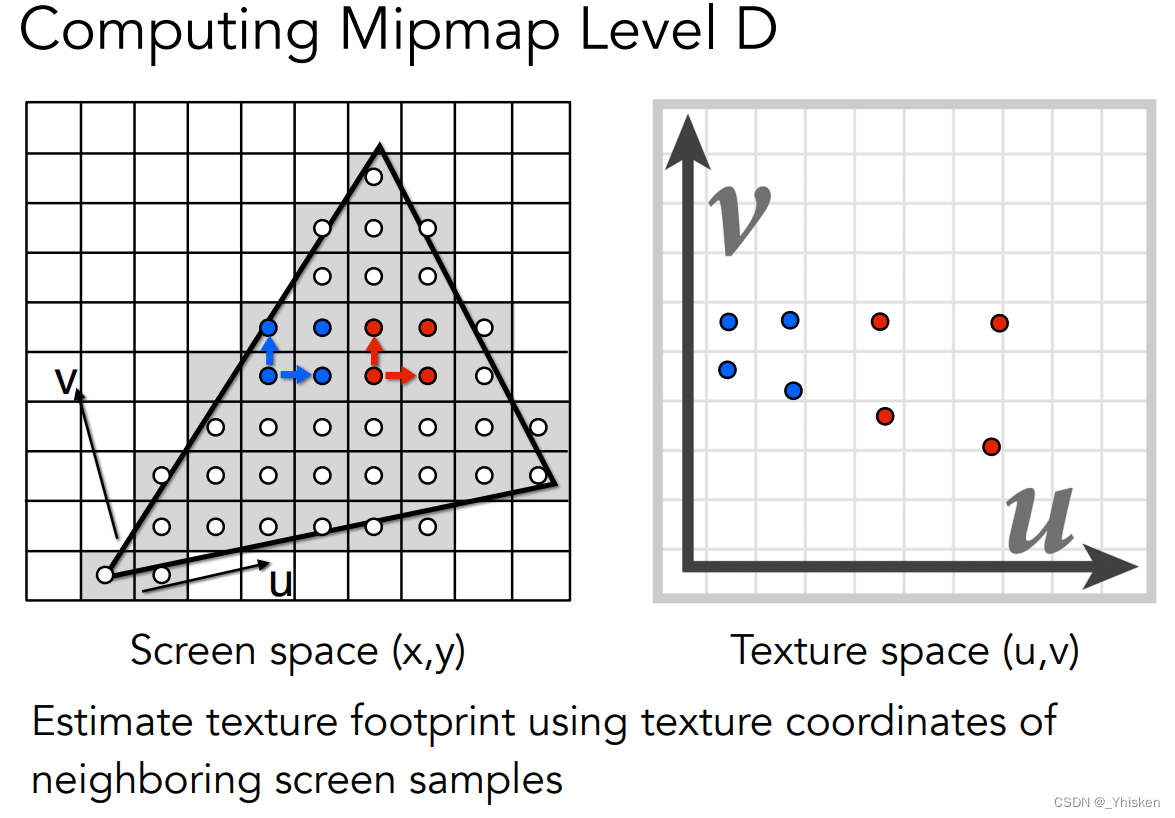
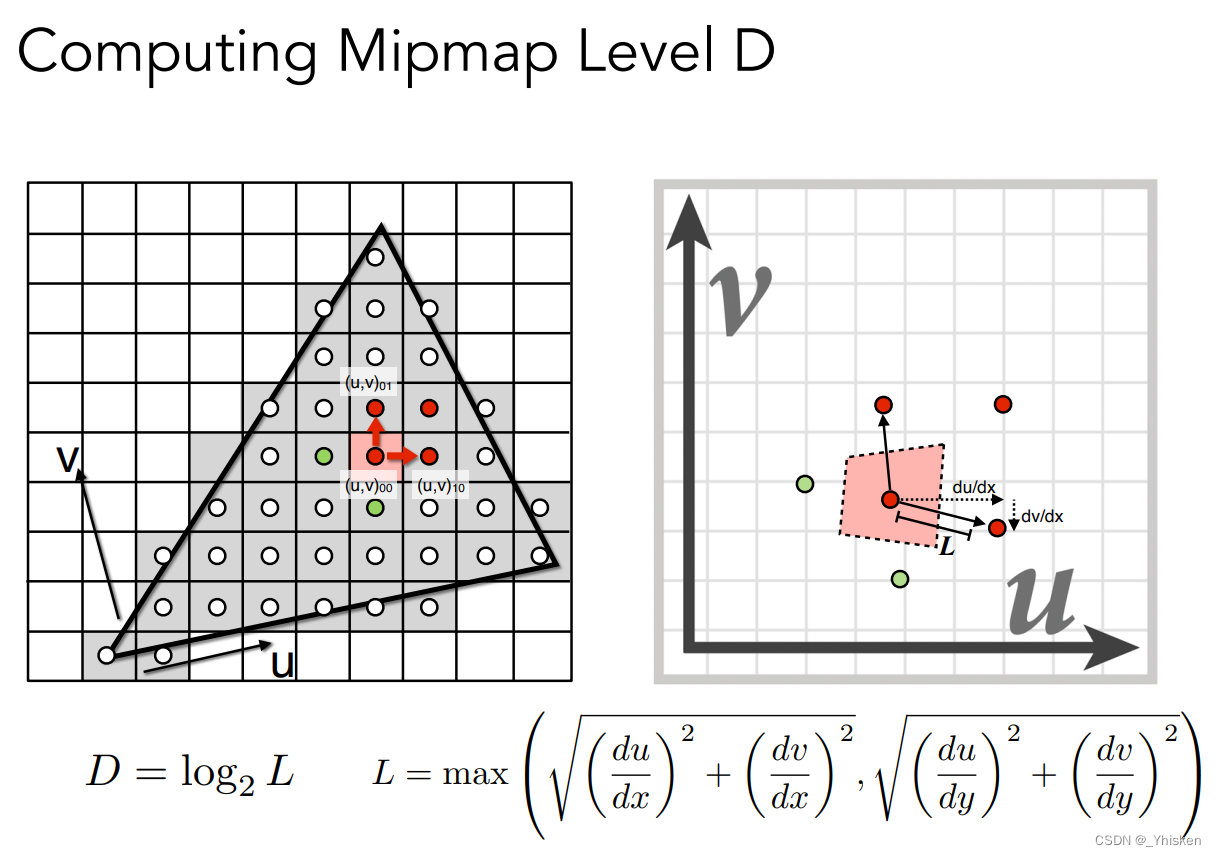
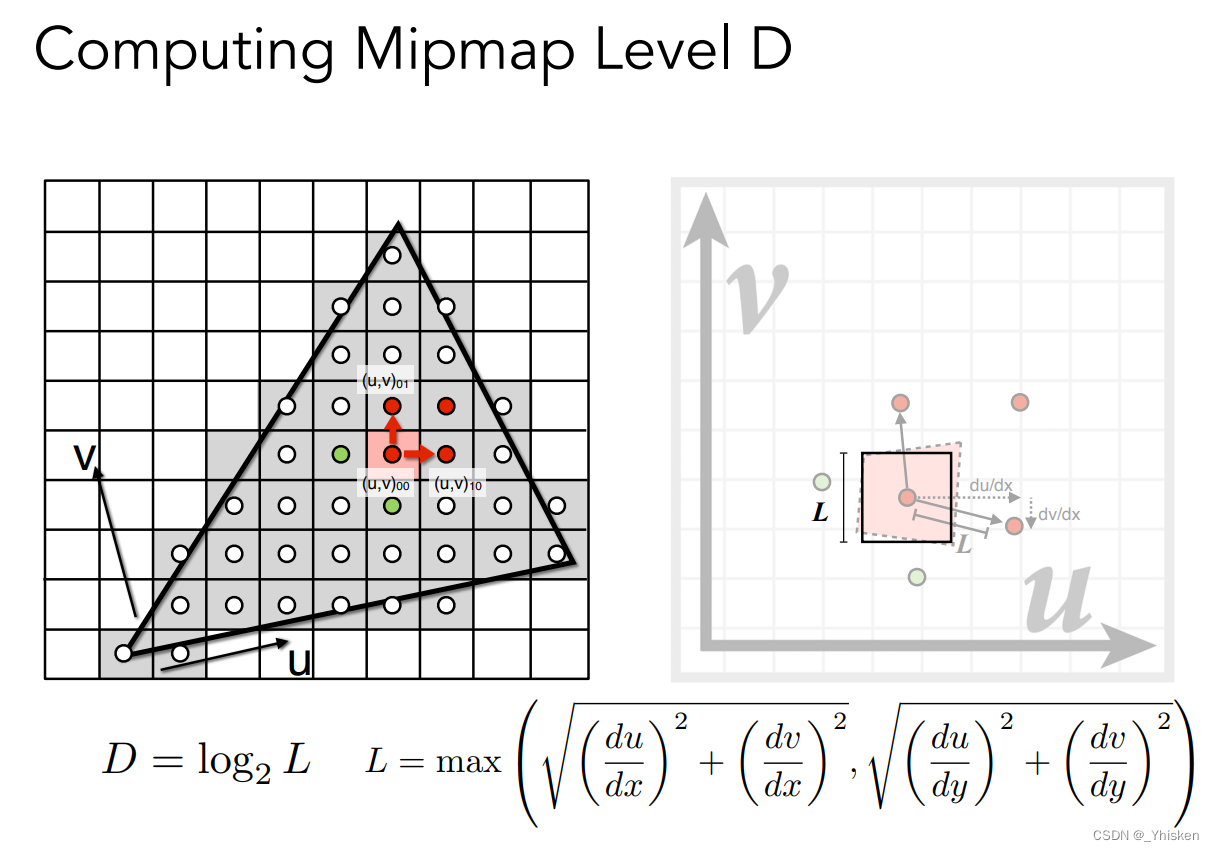
这里我们假设一个像素映射到纹理上的区域仍然是一个正方形的区域，而这个正方形区域的边长为L，L怎么求呢，假设我们求如上图的00的红色像素覆盖纹理区域，我们可以找临近像素的中心点同样映射到uv上，然后对他们求距离(图中为微分)，然后取较大的一个值来当作L就可以了。如上图所示。

那么如何通过知道我们覆盖正方形的大小来确定在哪层Mipmap上查询呢？很简单，假设我们正方形的面积是1x1，那么一定是在最原始的纹理上查询，而如果是4x4，那么一定在第二层上查询。以此类推在第D层上查询，则D=log2L。

但由此得到的结果是我们并不想看到的(如上图)，因为虽然有由远及近的渐变，但是中间还是有强硬的分界，也就是说Mipmap，只告诉了我们1，2层，却没有给我们1.5层，要解决这个问题也很简单，我们在这里继续使用插值运算。

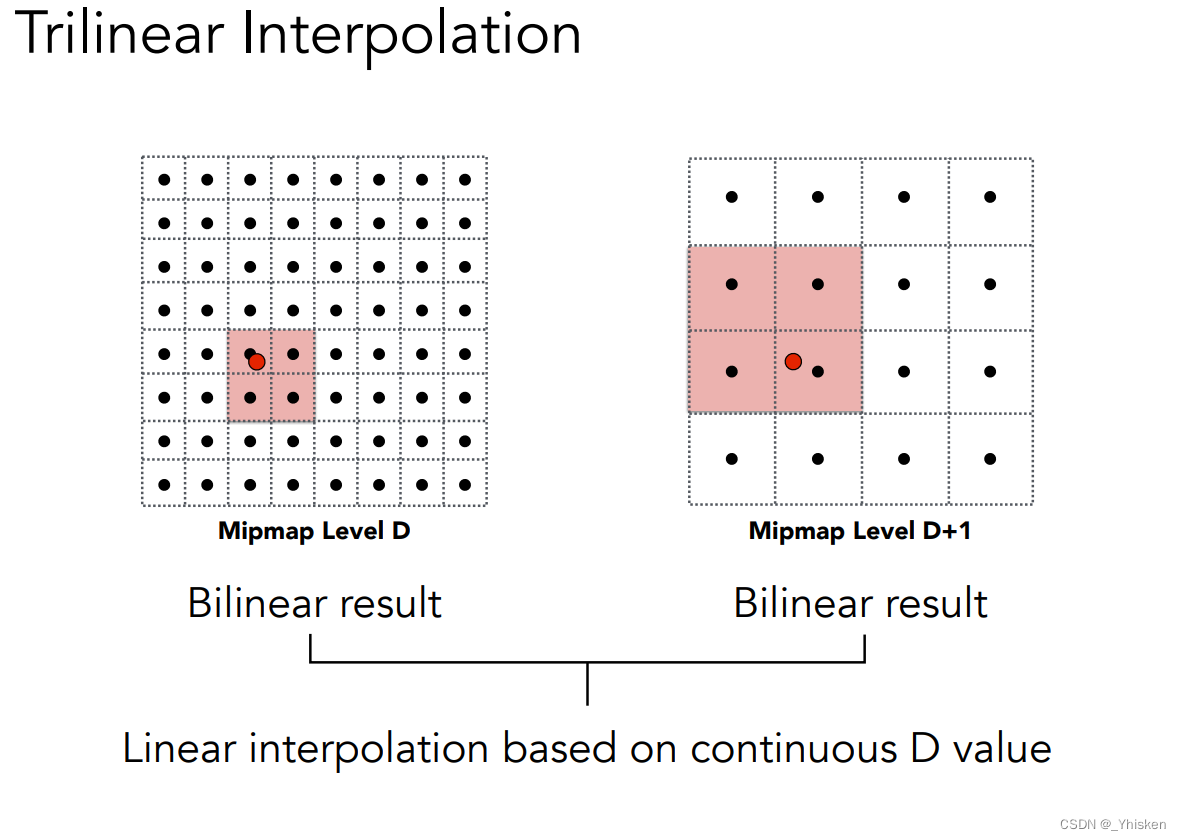
假设我们要查询1.8层的Mipmap，那么我们只需分别在第一层和第二层分别做双线性插值，再在两层已经做好插值的Mipmap层中间再做一次插值就可以得到1.8层对应的像素的颜色了。这种现在两层分别做双线性插值再在两层之间做插值的方法就叫做三线性插值。由此得到的结果正是我们需要的连续的，如下图。

可是当我们把Mipmap应用于我们最开始的图时，却发生了一些问题，远处似乎完全模糊掉了？

我们说过Mipmap并不准确而是近似，并且只能查询方块区域，所以才会造成这种问题。

(4)各向异性过滤—Anisotropic Filtering

各向异性过滤应用后的效果

上面的右图中我们可以看到，我们的Mipmap只是存在于这张图对角线上的一系列图片，也就是正方形，而各向异性过滤多了一些处理，它可以查询不只正方形，还有矩形区域。

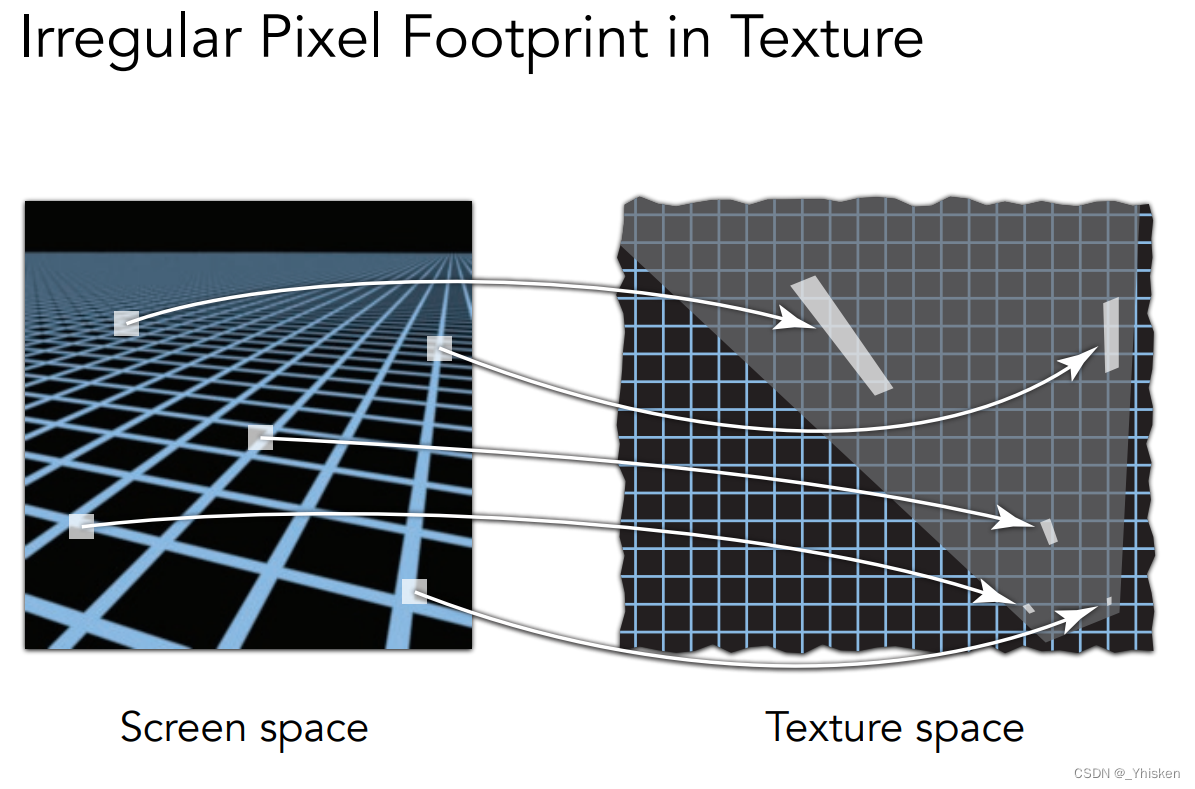
上图中表示，我们像素覆盖到纹理的区域形状可能各不相同，不一定都是正方形。而Mipmap却只能查询正方形范围，应用各向异性过滤之后，我们扩展到了可以查询矩形范围，所以会得到更好的结果。但是如果查询区域是一个平行四边形或者其他形状呢？各向异性过滤显然也解决不了。

各向异性过滤也有2x，4x，16x......，和Mipmap相同，这表示储存的层数，但和Mipmap不同的是，各向异性过滤的储存空间最终收敛到原来的3倍而不是4/3，但同样的，它并不会造成性能的损耗，而只有显存的开销。

(5)EWA过滤

EWA过滤可以把任何一个不规则形状拆成很多不同的圆形来覆盖这个不规则形状，然后多次查询不同的圆形，最后覆盖这个不规则形状，而代价就是耗时，因为要多次查询。

三、总结

本篇为大家带来了三角形的重心坐标插值计算，和应用纹理中的一些问题，如纹理过小，纹理过大的一些处理方法，计算机图形学的发展进步在今天远不止于此，本篇介绍的一些方法也只是冰山一角，有兴趣的朋友可以取寻找解决这些问题的更高级的方法。本篇主要是着重解释了GAMES101所讲的内容。那么下一篇为大家带来纹理贴图的高级应用，如凹凸贴图，法线贴图等，它们在游戏等3D渲染中同样有着很大的作用。那么下篇见，谢谢阅读。