红黑树RBT(Read Black Tree)小结

顺序搜索

线性搜索：跟队列中一个个元素顺序比较
时间复杂度是O(n)
存在的问题：元素多时搜索很慢

二分搜索(Binary Search)

队列中的元素有序，比如从小到大
每次把队列一分为二，每次跟队列中的中间元素比较
时间复杂度是O(log2/logn)
存在的问题：为了保证有序，每次插入/删除元素需要移动大量元素

二叉查找树BST(Binary Search Tree)

二叉树：任意一个结点左右最多只有两个子树
二叉查找树：任意结点左子树的元素都小于又子树的节点
时间复杂度：O(h)
特点：
- 查找效率和二分查找是一样的
- 插入/删除不需要移动大量元素
存在的问题：在极端情况下，树的高度会是元素的个数，时间复杂度变成O(n)

平衡二叉树AVL

Named after inventors Adelson-Velsky and Landis
在这里插入图片描述

AVL名字是根据三个发明者开头字母组成
平衡：任何一个结点左右子树的高度差不能超过1
在二叉查找树的基础上，通过平衡左右两边子树的高度，从而限制整个树的高度
高度：log2/logn+1
时间复杂度：O(log2/logn)
平衡操作分类：LL、RR、LR、RL
左旋：逆时针旋转
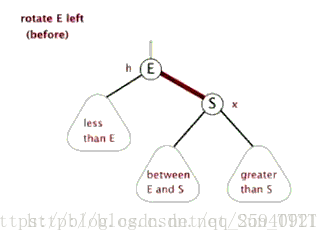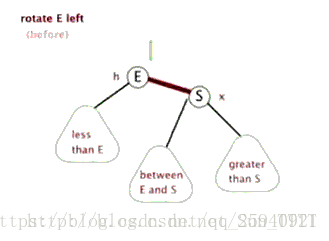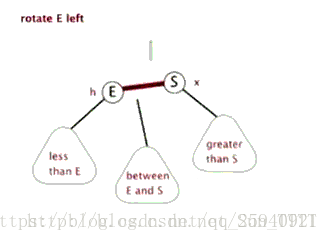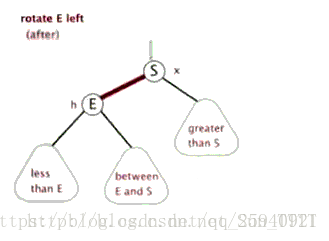
右旋：顺时针旋转
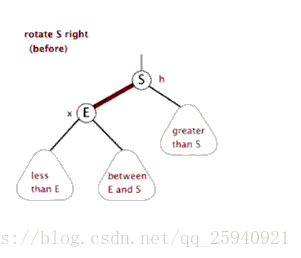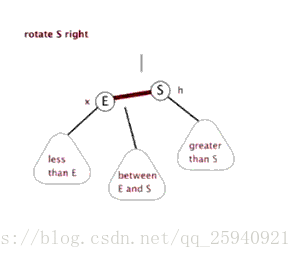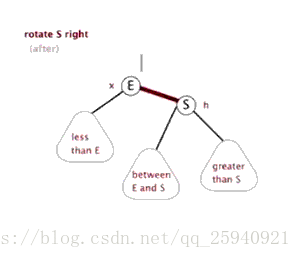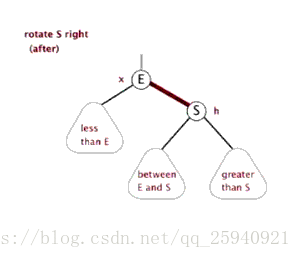
LL型：左孩子的左子树上插入结点，进行右旋操作
RR型：右孩子的右子树上插入结点，进行左旋操作
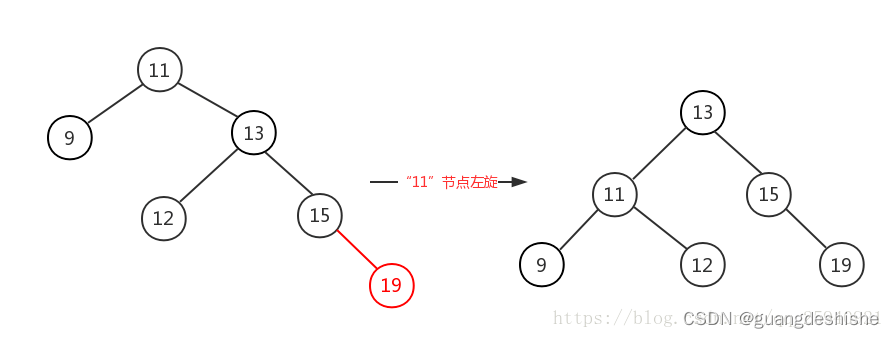
LR型：左孩子的右子树上插入结点，先左旋，后右旋
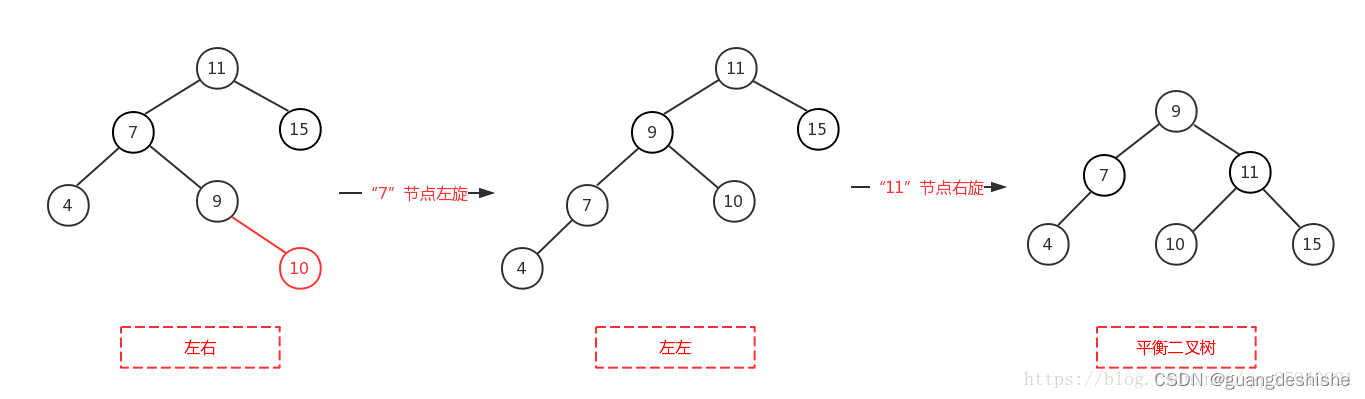
RL型：右孩子的左子树上插入结点，先右旋，后左旋
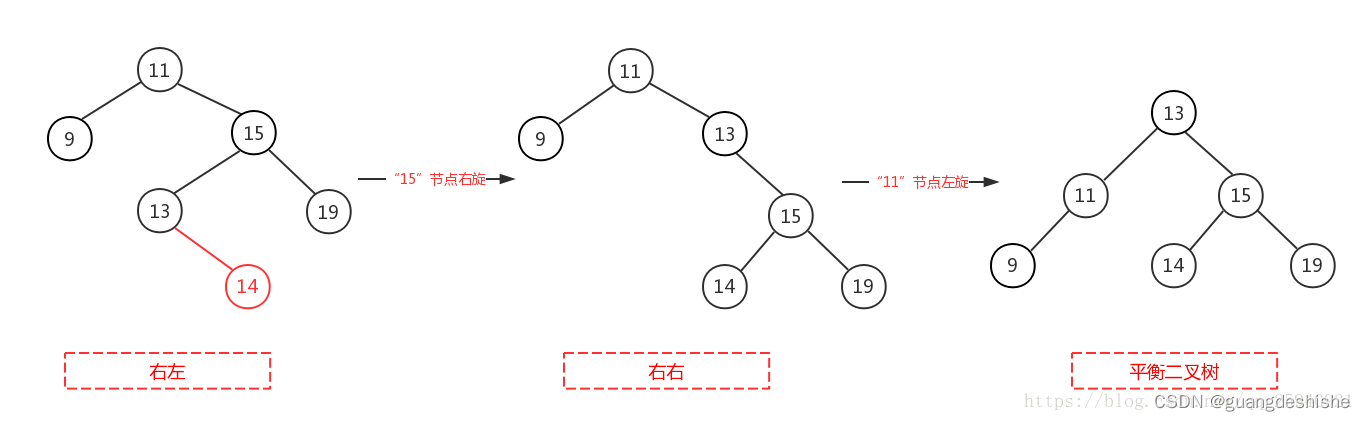
存在的问题：插入/删除会导致频繁的对元素平衡操作

红色树RBT(Read Black Tree)

红黑树是一种自平衡二叉查找树，每个结点不是红色就是黑色
相比AVL树，红黑树在插入和删除时需要旋转的次数更少，但是平衡性没有AVL好
- 当插入和删除操作比较少，查找比较多时，由于平衡性更高，意味着树的高度会更低；使用AVL树更合适
- 当插入和删除操作都比较多时，更适合红黑树
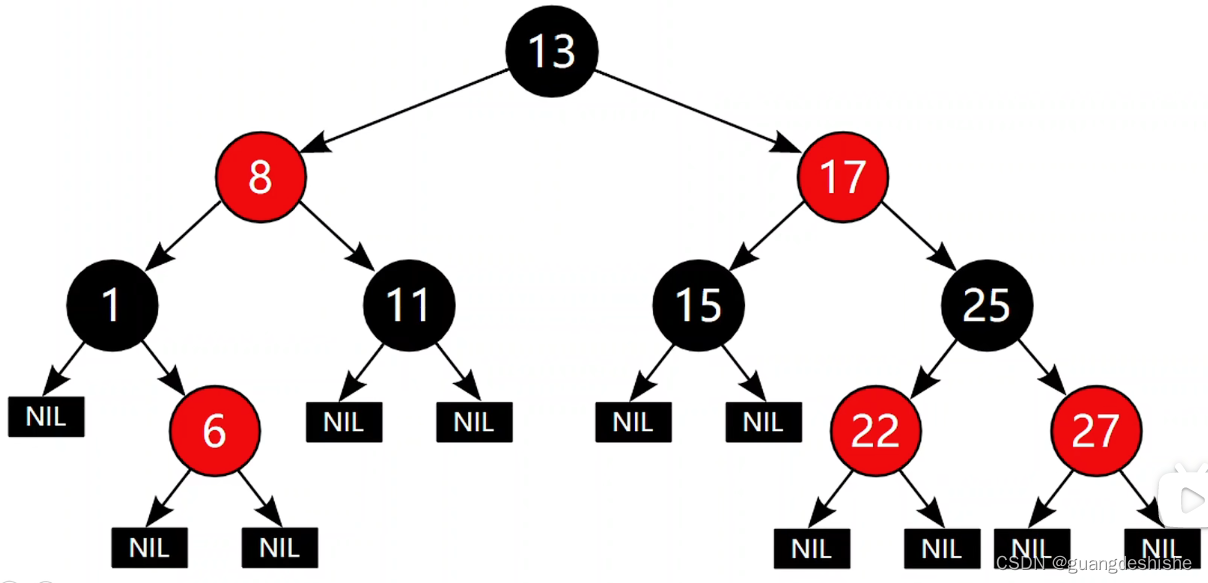
红黑树特点：
- 每个结点，不是红色就是黑色
- 红属性：红色结点的子结点一定是黑色的
  - 也就是不能连续两个是红色的
  - 黑色的可以连续都是黑色
- 黑属性：根结点一定是黑色的
  - 叶子结点都是不存储数据的黑色结点
  - 从每个结点出发，到所有叶子结点的路径上的黑色结点个数都相同
高度：2*log(n+1)
时间复杂度：O(logn)
bh黑色高度：从一个结点到它的叶子结点所经过的黑色结点个数
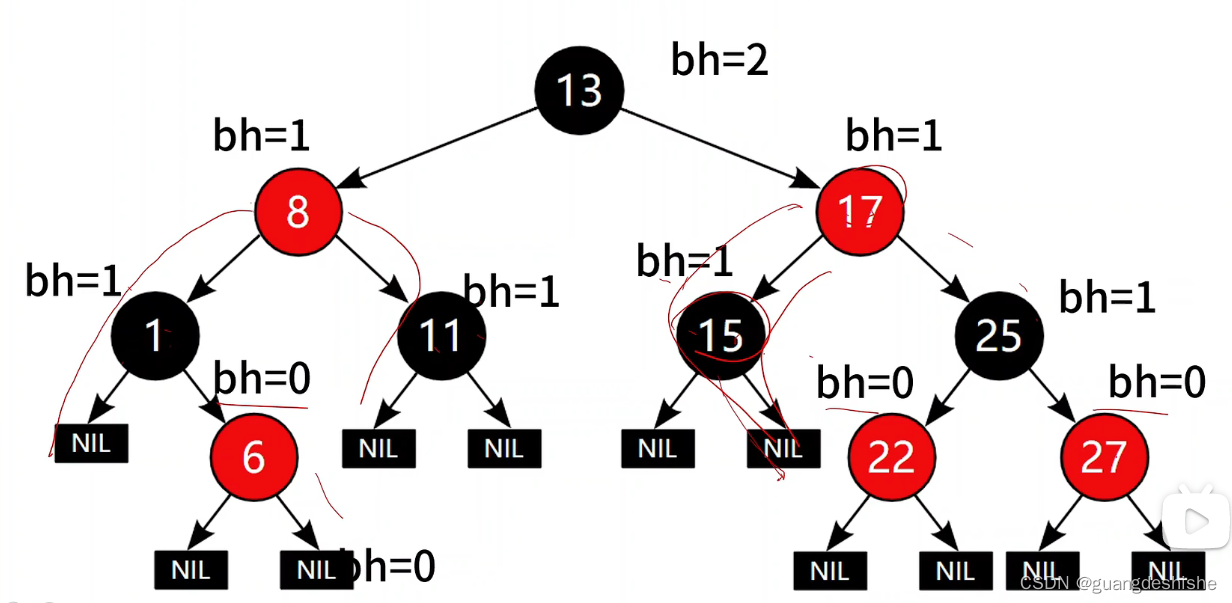
插入元素：
- 如果插入的是第一个根元素，标记为黑色，结束
- 新插入的元素先标记成红色
- 如果插入后父亲是黑色的，则不需要处理，结束
- 如果插入后父亲是红色的，同时父亲的兄弟也是红色的：
  - 1.父亲和父亲的兄弟都变成黑色
  - 2.如果父亲的父亲作为根结点则不用变色，否则要变色
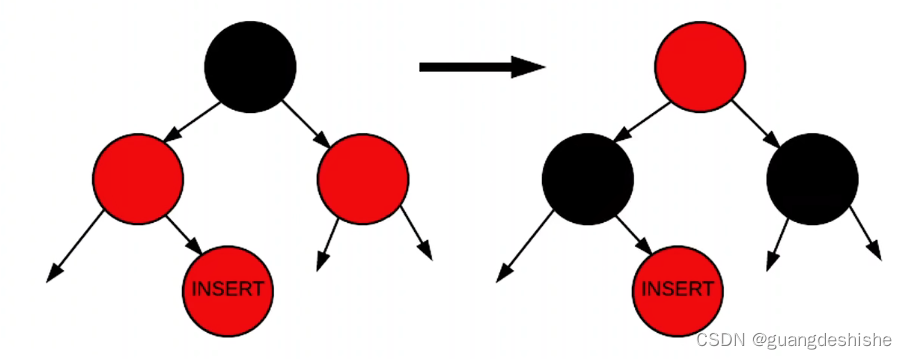
- 如果插入后父亲是红色的，但是父亲的兄弟不存在或者是黑色的
  - 1.先旋转平衡后变色
  - 2.具体是先将插入的元素变成黑色
  - 3.再将刚插入元素是父节点的父节点变成红色

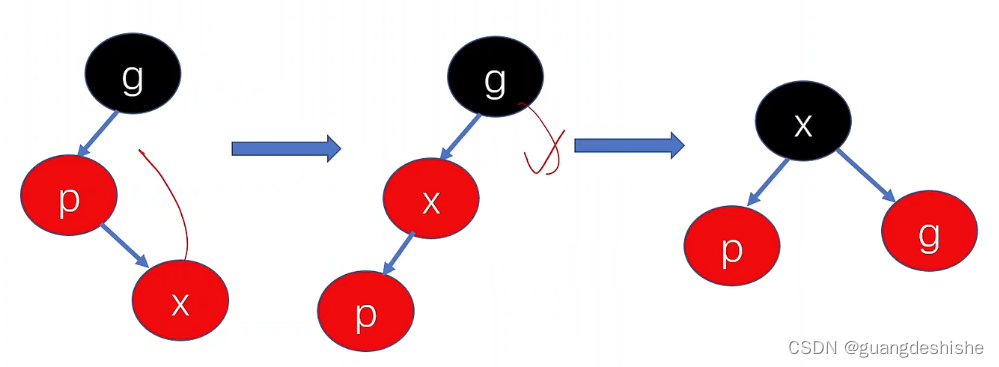
其他：

一般情况不允许有重复元素，有重复元素插入时会失败
如果需要保留重复元素，可以考虑在结点结构中增加一个字段记录元素重复次数
结点和节点的区别：
- 节点：一般是指某个处理中心，比如网络中的某个节点：计算机、路由器等等
- 结点：某一个交叉点，没有特殊作用，一般算法中应该用这个结点

红黑树小结

红黑树是一种自平衡二叉查找树，平衡性相对AVL树没有那么严格，但是在插入、删除、搜索综合性能方面更加优秀
红色树主要有三个特点：
- 根结点和叶子结点都是黑色的
- 相邻的两个结点不能同时为红色
- 每一个结点到叶子结点经过的每个路径上的黑色结点个数都相同

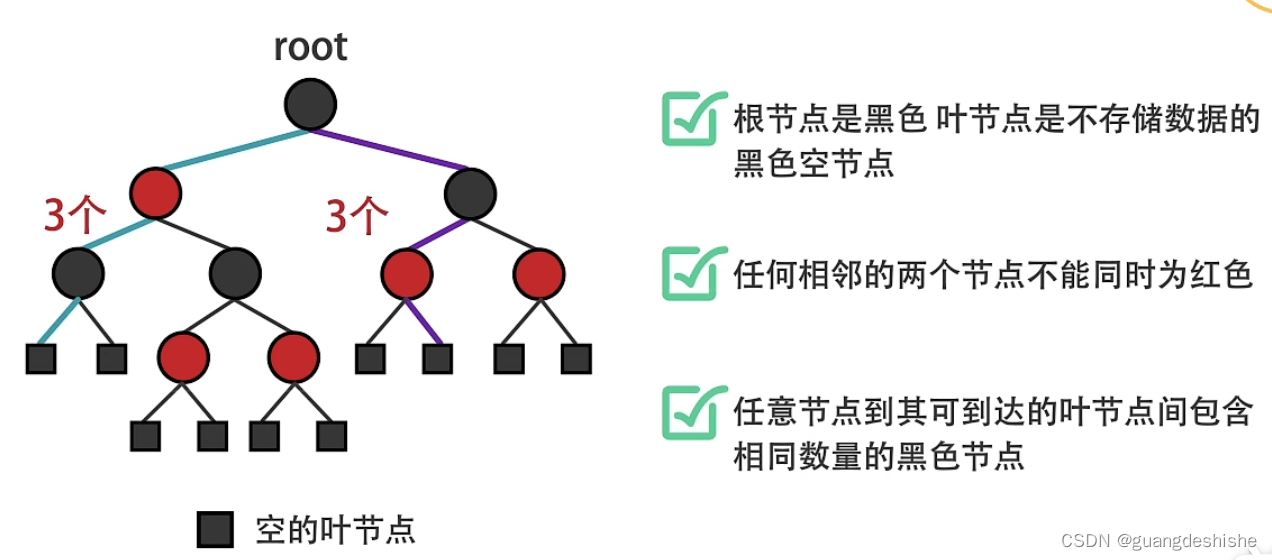
在这里插入图片描述

最多高度：2*log(n+1)；时间复杂度：logn
插入元素：
- 如果插入的是第一个根元素，则标记为黑色，结束
- 插入的元素先标记为红色
- 如果插入元素后，它的父结点是黑色的，则结束
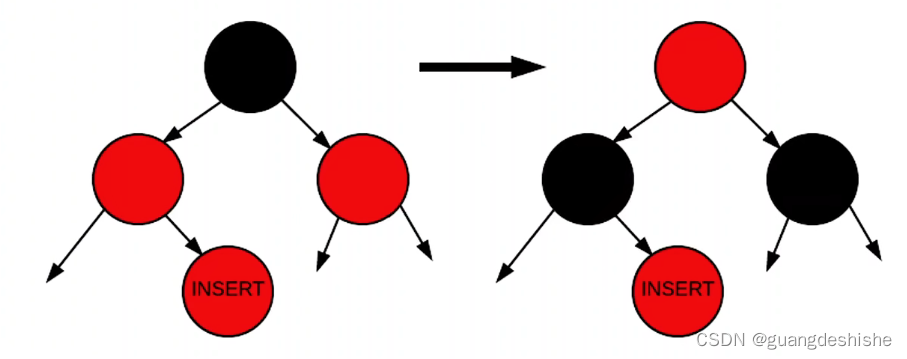
- 如果插入元素后，它的父结点和父结点的兄弟都是红色的
  - 先将父结点和父结点的兄弟都变成黑色
  - 父节点的父节点如果不是根结点则要变成红色
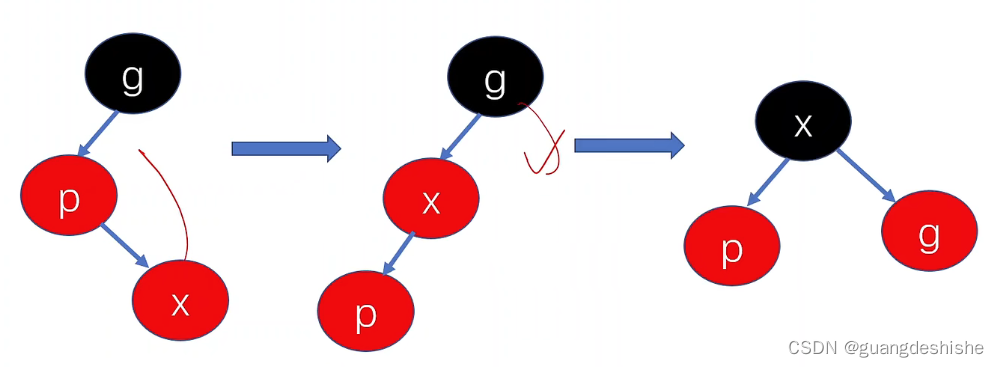
- 如果插入元素后，它的父节点是红色，但是父节点的兄弟为空或者为黑色
  - 1.先旋转平衡后变色
  - 2.具体是先将插入的元素变成黑色
  - 3.再将刚插入元素是父节点的父节点变成红色