一. 简介

在上篇文章中，已经介绍了如何使用booth算法生成部分积了，那么在这篇文章中将介绍如何使用加法树对部分积进行压缩。加法树压缩有多种形式，常见的是Wallace压缩，也是赛题中介绍一种方法。
感兴趣的可以，可以研究研究哦。

二. Wallace压缩

在Wallace压缩中，常见的压缩方法有3:2压缩和4:2压缩，罕见的有5:2压缩。

3:2压缩的表达式和框图如下

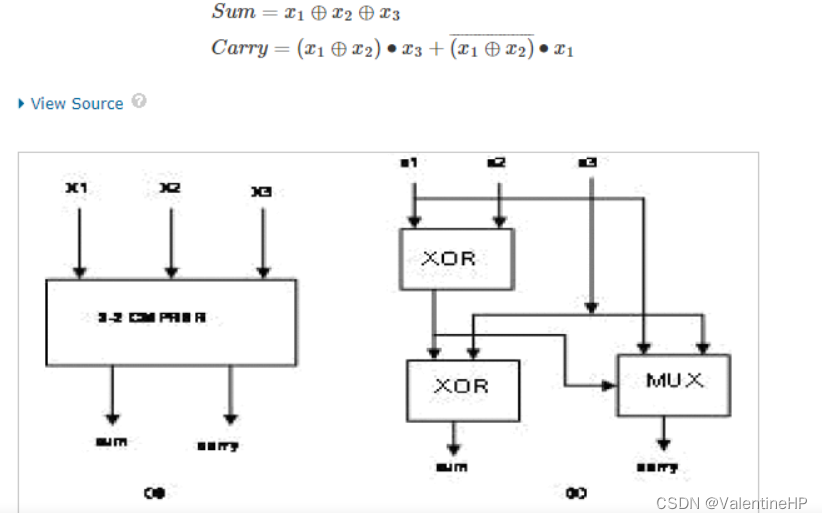
4:2压缩的表达式和框图如下

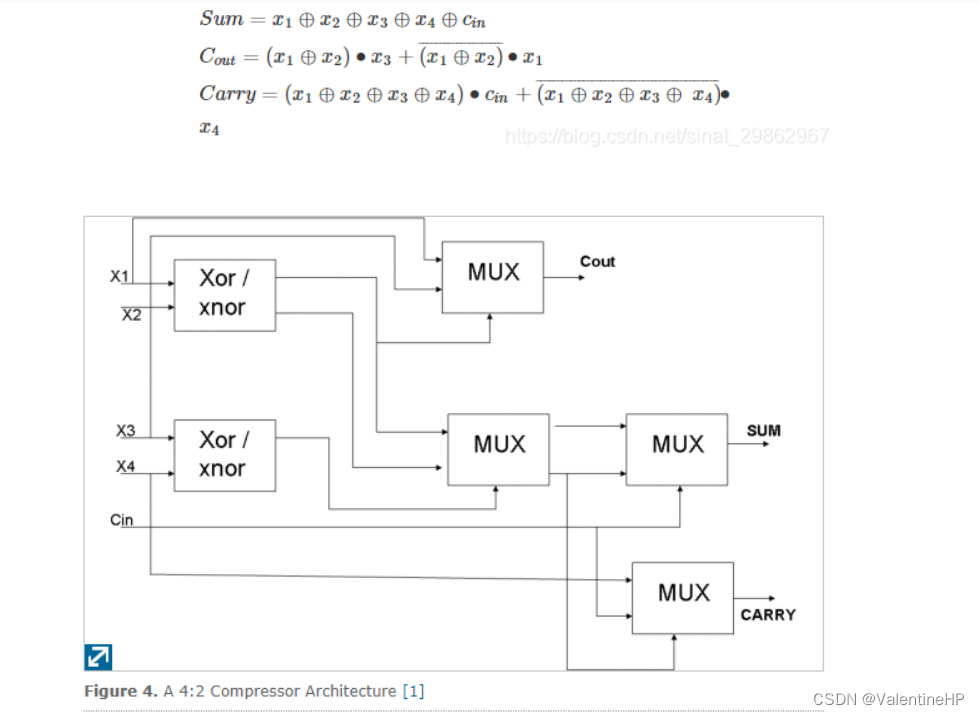
5:2的就不介绍了，这里详细说说4:2压缩器，因为经过的算法，生成的部分积恰好有8个，经过三个4:2压缩器就可以了。而使用3:2压缩则需要更深的结构，因此在我的设计中没有使用。

4:2压缩就是输入1bit的4个数据以及1bit进位，然后输出1bit的两个数据和一个进位。我们需要32bit的压缩器时，只需要将1bit的4:2压缩级联起来即可，上一个的Cout输入到下一个的Cin即可。最后的结果需要将Carry左一位。代码实现起来如下。

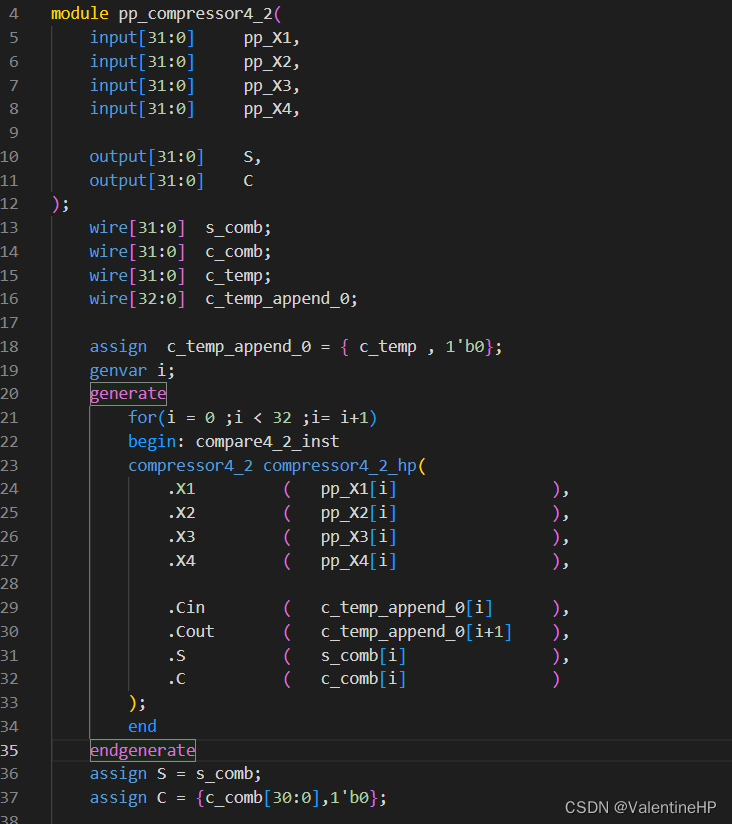
就将4个部分积压缩到了两个部分积，使用三个这样的压缩器，最终就得到了2个部分积。

压缩这里为什么不直接使用加法器呢？通过压缩器的结构即可明白。

三. 结果

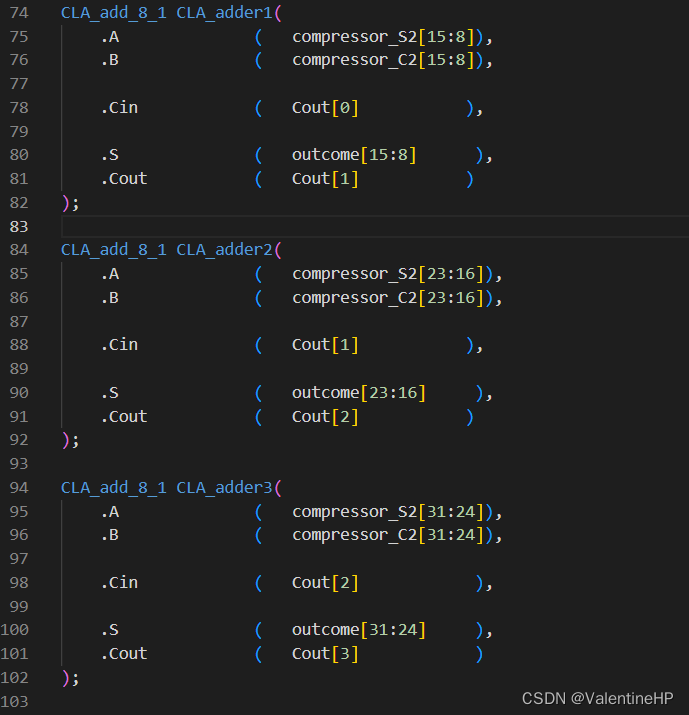
最后使用一个32bit的加法器，将最后两个部分积相加即可。这里使用了四个8bit的超前进位加法器串联成的32bit加法器。超前进位加法器可以有效减少因为进位而带来的延时。

ps: 另外可以通过选择加法器，增加额外的两个8bit加法器，以及一个选择器，进一步降低延时。

四. 小结

简单的介绍了一下定点乘法器的实现原理，以及实现过程。在此框架下想要对乘法器的性能进行优化，一般都是从两点出发，部分积的生成和部分积的压缩，在知网阅读相关论文，大部分都是从这两点进行优化。后面我也将从这两点进行优化以及程序上，希望能有所提升。

目前整个设计大概消耗了2100多个与非门 和 800多个非门（转化为与非门）使用yosys工具可以自动统计，使用DC工具综合出只使用了800多个门，计算延时为16ns(在FPGA上)，仿真图如下。还达不到比赛的要求，后续会分享优化的版本。感兴趣的可以一起研究研究。

关注回复 定点乘法器基础版本 获取完整代码