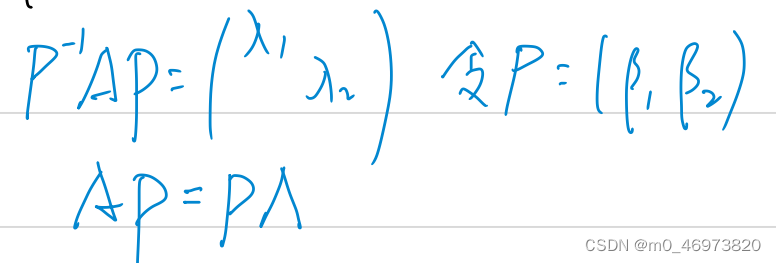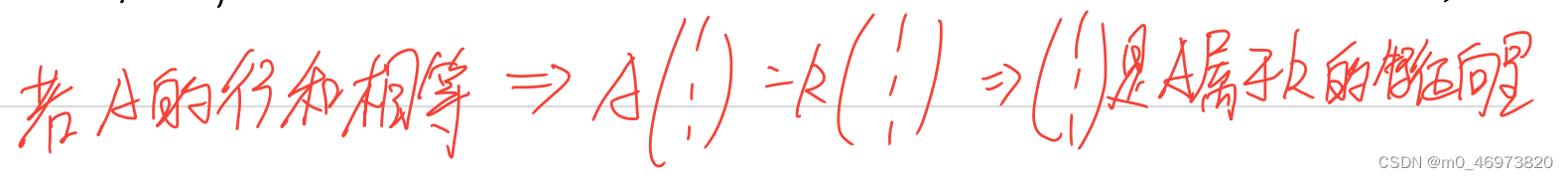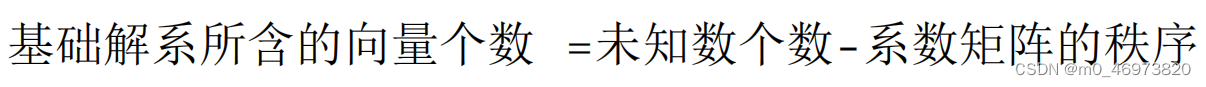A=[1 1 1 1;1 1 -1 -1;1 -1 1 -1;1 -1 -1 1];
V=eig(A);
E=eye(4);b=zeros(4,1);
X1=A-V(1)*E;Y1=null(A-V(1)*E,b);
Y2=null(A-V(2)*E,b);
%% 验证
Y4(:,1)*V(4)==A*Y4(:,1);
norm(Y4(:,1)*V(4)-A*Y4(:,1));
%% 验证
[V,D]=eig(A);
[V,D]=eig(sym(A));

>> [V,D]=eig(sym(A))
 
V =
 
[-1, 1, 1, 1]
[ 1, 1, 0, 0]
[ 1, 0, 1, 0]
[ 1, 0, 0, 1]
 
 
D =
 
[-2, 0, 0, 0]
[ 0, 2, 0, 0]
[ 0, 0, 2, 0]
[ 0, 0, 0, 2]

嗯，真帅！

 MATLAB生成正交矩阵 ，orth（A）计算A的正交基。

>> A=[2 2;2 5];
>> q=orth(A);
>> q'*A*qans =6.0000   -0.0000-0.0000    1.0000>> [V,D]=eig(sym(A))V =[-2, 1/2]
[ 1,   1]D =[1, 0]
[0, 6]

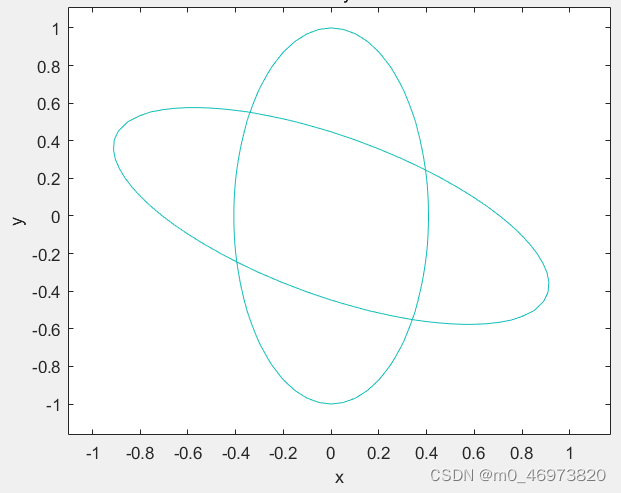
 蒙特卡洛法求椭圆面积（http://t.csdn.cn/7DVK8）

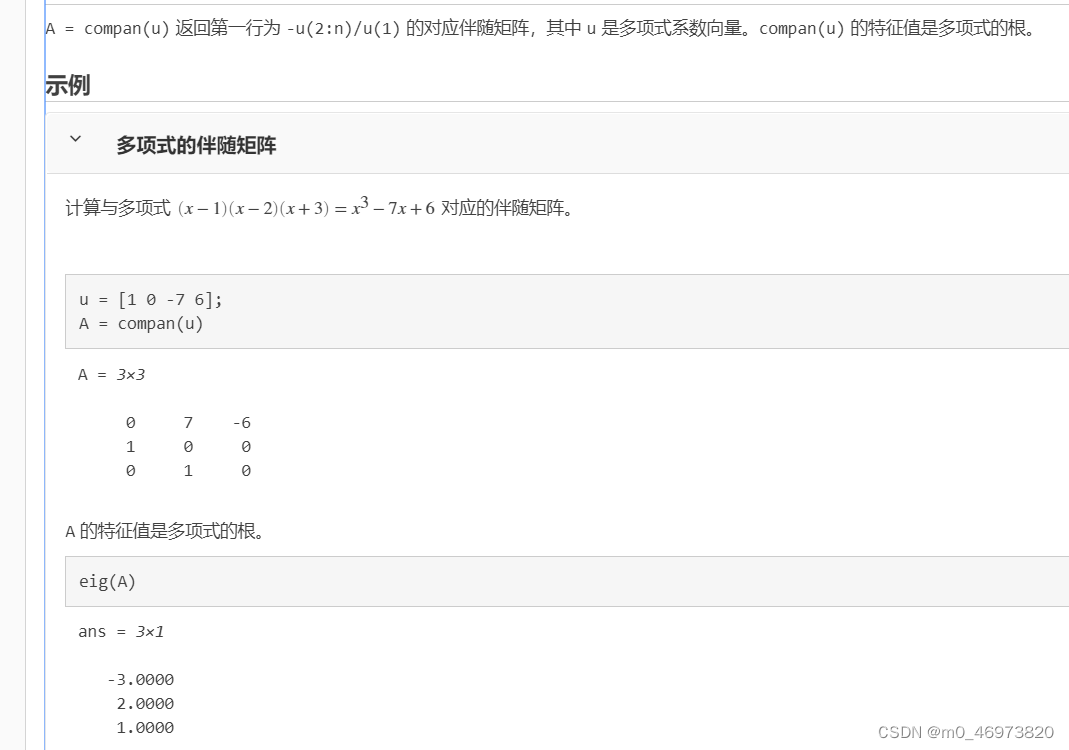
多项式的 伴随矩阵 的特征值是这个多项的根。

>> p=[1,0,-1,6];
>> A=compan(p);
>> eig(A)ans =-2.0000 + 0.0000i1.0000 + 1.4142i1.0000 - 1.4142i>> roots(p)ans =-2.0000 + 0.0000i1.0000 + 1.4142i1.0000 - 1.4142i

>> A=[3 -2 -4;-2 6 -2;-4 -2 3];
>> Astar=adjoint(A)Astar =14.0000   14.0000   28.000014.0000   -7.0000   14.000028.0000   14.0000   14.0000>> Astar=det(A)*inv(A)Astar =14.0000   14.0000   28.000014.0000   -7.0000   14.000028.0000   14.0000   14.0000>> Astar*Aans =-98.0000    0.0000         0-0.0000  -98.0000    0.0000-0.0000    0.0000  -98.0000

用代数余子式的定义求

function Astar = adjA(A)
% 输入方阵A，输出A的伴随矩阵Astar
[m,n] = size(A);
M = zeros(m,n);
if m == nfor i = 1 : mfor j = 1 : nX = A;X(i,:) = [];%去掉第i行X(:,j) = [];%去掉第j列M(i,j) = det(X)*(-1)^(i+j);%计算代数余子式endend
elseerror('输入必须为方阵'); 
end
Astar = M';
end

>> A=[3 -2 -4;-2 6 -2;-4 -2 3];
>> trace(A)ans =12>> det(A)ans =-98>> eig(A)ans =-277>> adjoint(A)ans =14.0000   14.0000   28.000014.0000   -7.0000   14.000028.0000   14.0000   14.0000

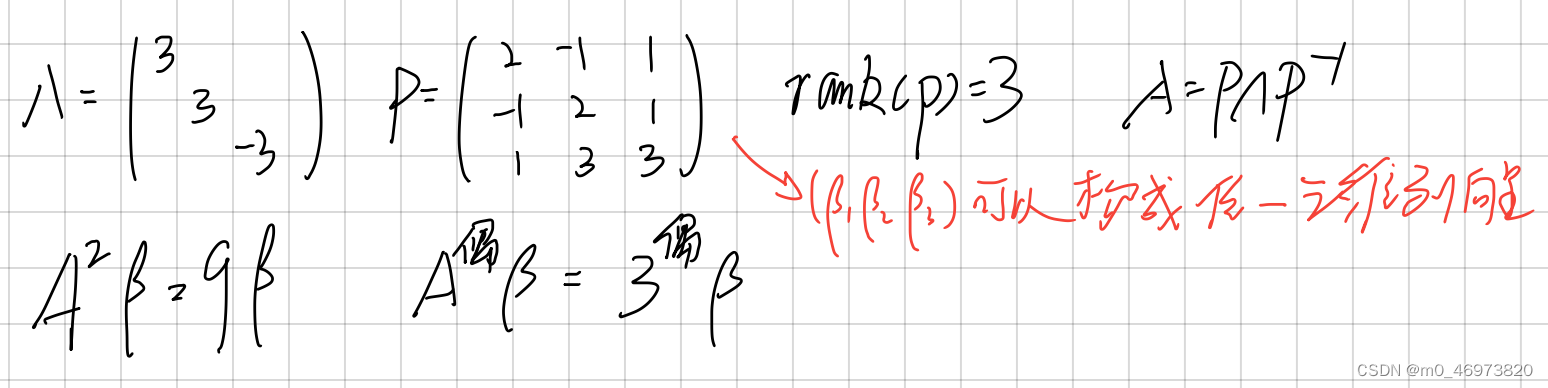
A的特征向量、特征值
>> A=[3 -2 -4;-2 6 -2;-4 -2 3];
>> [V,D]=eig(sym(A))V =[  1, -1/2, -1]
[1/2,    1,  0]
[  1,    0,  1]D =[-2, 0, 0]
[ 0, 7, 0]
[ 0, 0, 7]>> dot(V(:,1),V(:,2))ans =0

不同特征值对应的特征向量内积得0，垂直正交。

A逆的特征向量、特征值
>> An=inv(A);
>> [Vn,Dn]=eig(sym(An))Vn =[  1, -1/2, -1]
[1/2,    1,  0]
[  1,    0,  1]Dn =[-1/2,   0,   0]
[   0, 1/7,   0]
[   0,   0, 1/7]

A星的特征向量、特征值
>> Ax=adjoint(A);
>> [Vx,Dx]=eig(sym(Ax))Vx =[  1, -1/2, -1]
[1/2,    1,  0]
[  1,    0,  1]Dx =[49,   0,   0]
[ 0, -14,   0]
[ 0,   0, -14]>> det(A)ans =-98

fA的 特征向量、特征值
>> fA=A^3+2*A^2-A+5*eye(3);
>> [fV,fD]=eig(sym(fA))fV =[  1, -1/2, -1]
[1/2,    1,  0]
[  1,    0,  1]fD =[7,   0,   0]
[0, 439,   0]
[0,   0, 439]

A的相似矩阵的特征向量、特征值
>> p=[1 -2 1;2 4 -1;3 2 -2];
>> det(p)ans =-16.0000>> B=inv(p)*A*p;
>> [BV,BD]=eig(sym(B))BV =[ 9/4, -2/5, 3/10]
[-3/8,    1,    0]
[   1,    0,    1]BD =[-2, 0, 0]
[ 0, 7, 0]
[ 0, 0, 7]

>> A=[3 -2 -4;-2 6 -2;-4 -2 3];
>> [P,L]=eig(sym(A));
>> A*Pans =[-2, -7/2, -7]
[-1,    7,  0]
[-2,    0,  7]>> P*Lans =[-2, -7/2, -7]
[-1,    7,  0]
[-2,    0,  7]

>> p=[2 -1 1;-1 2 1;1 3 3]p =2    -1     1-1     2     11     3     3>> rank(p)ans =3>> j=[3 0 0;0 3 0;0 0 -3]j =3     0     00     3     00     0    -3>> A=p*j*inv(p)A =-7.0000  -14.0000    6.0000-10.0000  -11.0000    6.0000-30.0000  -42.0000   21.0000

>> b=[1 -1 3]'b =1-13

>> A^8*bans =1.0e+04 *0.6561-0.65611.9683>> ans./bans =1.0e+03 *6.56106.56106.5610>> 3^8ans =6561

>> A=magic(3)A =8     1     63     5     74     9     2>> [P,L]=eig(sym(A));
>> [P,L]=eig(sym(A))P =[1, - 24^(1/2)/5 - 7/5, 24^(1/2)/5 - 7/5]
[1,   24^(1/2)/5 + 2/5, 2/5 - 24^(1/2)/5]
[1,                  1,                1]L =[15,        0,         0]
[ 0, 24^(1/2),         0]
[ 0,        0, -24^(1/2)]

>> A=[1 1 1];
>> b=[0];
>> x=null(A,'r')x =-1    -11     00     1

实对称矩阵

>> A=round(5*rand(3));
>> A+A'ans =10     6     66     4     66     6    10

完美的结论

矩阵的行阶梯，极大无关组

>> s1=[1 2 2]';s2=[0 -1 1]';s3=[-4 1 1]';s4=[2 -5 3]';
>> s=[s1,s2,s3,s4];
>> [R,jb]=rref(s);
>> s(:,jb)ans =1     0    -42    -1     12     1     1>> RR =1.0000         0         0   -0.22220    1.0000         0    4.00000         0    1.0000   -0.5556

说明s4可有s1、s2、s3表示

伴随是啥？