变分推断 (Variational Inference)

变分推断属于对隐变量模型 (Latent Variable Model) 处理的一种技巧，其概率图如下所示

我们将 X={x1,...xN}X=\{ x_1,...x_N \}X={x1​,...xN​} 看作是每个样本可观测的一组数据，而将对应的 Z={z1,...,zN}Z=\{z_1,...,z_N\}Z={z1​,...,zN​} 看作是该组数据对应的高维空间下的对应样本点，例如使用 $X$ 表示一个班同学的所有成绩，而将 $Z$ 看作是同学的学习能力。对于更复杂的一些情况，例如图像生成任务，使用 $X$ 表示数据集中的每张图像，而使用 $Z$ 表示更高维的信息，例如基于类别/语义等控制信息。

对于生成任务，我们经常希望利用观测数据 $X$ 建模随机变量 $x$ 的真实分布 $p(x)$，使用 $z$ 来辅助概率推导，那么核心点在于计算两个条件概率分布 $p(x|z)$ 与 $p(z|x)$，通常可以使用一些先验知识假定 $p(x|z)$ 服从某种概率分布（例如对于学习能力为 $g$ 的同学成绩假定服从在 $g$ 附近的高斯分布），但对于 $p(z|x)$，注意到
$$p(z|x)=\frac{p(z)p(x|z)}{p(x)}$$
$z$ 是辅助建模的变量，可以假定其服从某已知的分布，但对于归一化项 $p(x)$，有
$$p(x)={\int }_{z}p(x,z)dz={\int }_{z}p(z)p(x|z)dz$$
由于 $z$ 是一个非常高维的信息，$p(x)$ 是很难直接计算积分进行处理的，所以 $p(z|x)$ 也是很难处理的，我们通常使用优化的方法来拟合出概率分布 $p(z|x)$

首先，我们考虑随机变量 $z$ 与 $x$ 之间的关系，假定 $p(x)$ 表示真实的数据分布，即我们观测到的数据 $x\sim p(x)$，$q(z|x)$ 为任一条件概率分布（通常是使用模型拟合出来的分布），有
$$\begin{array}{rl}\log p(x)& =\log p(x,z)-\log p(z|x)\\ & =\log \frac{p(x,z)}{q(z|x)}-\log \frac{p(z|x)}{q(z|x)}\end{array}$$
对左右两式计算关于隐变量 $z$ 的期望，有
$$\begin{array}{rl}\text{left}& ={\mathbb{E}}_{z\sim q(z|x)}[\log p(x)]=\log p(x){\int }_{z}q(z|x)dz=\log p(x)\\ \text{right}& ={\mathbb{E}}_{z\sim q(z|x)}[\log \frac{p(x,z)}{q(z|x)}-\log \frac{p(z|x)}{q(z|x)}]={\int }_{z}q(z|x)\log \frac{p(x,z)}{q(z|x)}dz+{\int }_{z}q(z|x)\log \frac{q(z|x)}{p(z|x)}dz\\ & ={\int }_{z}q(z|x)\log \frac{p(x,z)}{q(z|x)}dz+\text{KL}(q(z|x)||p(z|x))\end{array}$$
其中 ${\int }_{z}q(z|x)\log \frac{p(x,z)}{q(z|x)}dz$ 被称作是信心下界 (Evidence Lower Bound)，简单记作 ELBO，名字来源是由于KL散度满足恒大于等于0的性质，因此有 $\log p(x)\ge \text{ELBO}$，当 $q(z|x)=p(z|x)$ 时取等，因此我们有如下公式
$$\begin{array}{r}\log p(x)=\text{ELBO}+\text{KL}(q(z|x)||p(z|x))\ge \text{ELBO}\end{array}$$
如果我们希望 $q(z|x)$ 逼近真实条件概率分布 $p(z|x)$，在观测数据 $x$ 给定的情况下，最小化KL散度等价于最大化ELBO

假定 $q(z|x)$ 表示的概率分布由参数 $\varphi$ 决定（例如使用神经网络表示 $q_{\varphi }$，我们一般不改变网络结构，而只针对参数进行优化），那么该拟合问题的优化目标如下所示
$$\hat{\varphi }=\arg \underset{\varphi }{\max }\text{ELBO}$$
如果我们采用随机梯度下降法来进行优化 (Stochastic Gradient Varational Inference)，首先要计算 $\varphi$ 的导数
$$\begin{array}{rl}{▽}_{\varphi }\text{ELBO}& ={▽}_{\varphi }{\int }_z{q}_{\varphi }(z|x)\log \frac{p(x,z)}{q_{\varphi }(z|x)}dz\\ & ={\int }_z{▽}_{\varphi }{q}_{\varphi }(z|x)\log \frac{p(x,z)}{q_{\varphi }(z|x)}dz+{\int }_z{q}_{\varphi }(z|x){▽}_{\varphi }\log \frac{p(x,z)}{q_{\varphi }(z|x)}dz\end{array}$$
注意到，对于第二项，有
$${\int }_z{q}_{\varphi }(z|x){▽}_{\varphi }\log \frac{p(x,z)}{q_{\varphi }(z|x)}dz=-{\int }_z{q}_{\varphi }(z|x){▽}_{\varphi }\log q_{\varphi }(z|x)dz=-{\int }_z{▽}_{\varphi }{q}_{\varphi }(z|x)dz=-{▽}_{\varphi }{\int }_z{q}_{\varphi }(z|x)dz=0$$
因此，有如下等式
$$\begin{array}{rl}{▽}_{\varphi }\text{ELBO}& ={\int }_z{q}_{\varphi }(z|x){▽}_{\varphi }\log q_{\varphi }(z|x)\log \frac{p(x,z)}{q_{\varphi }(z|x)}dz\\ & ={\mathbb{E}}_{z\sim q_{\varphi }(z|x)}[{▽}_{\varphi }\log q_{\varphi }(z|x)\log \frac{p(x,z)}{q_{\varphi }(z|x)}]\end{array}$$
使用 Monto-Carlo 采样方法计算期望，即 $z_i\sim q_{\varphi }(z|x)(i=\mathrm{1...}L)$
$${▽}_{\varphi }\text{ELBO}\approx \frac{1}{L}\sum _{i=1}^L{▽}_{\varphi }\log q_{\varphi }(z_i|x)\log \frac{p(x,z_i)}{q_{\varphi }(z_i|x)}$$
注意到，式子中包含 ${▽}_{\varphi }\log q_{\varphi }(z_i|x)$，以下为 $y=\log (x)$ 的函数图像

在 $x$ 较小时值的变化范围很大，因此直观上来看 ${▽}_{\varphi }\log q_{\varphi }(z_i|x)\log \frac{p(x,z_i)}{q_{\varphi }(z_i|x)}$ 方差较大，对于每个 $x$ 都需要大量采样 $z$ 才能得到一个较为准确的期望值，实际应用时存在较大困难，因此引入如下重参数化技巧 (Re-parameterization)

重参数化技巧：我们希望解耦随机变量 $z$ 中的随机性与 $\varphi$ 之间的关系，使得计算期望时随机变量服从的概率分布 $z\sim q_{\varphi }(z|x)$ 转变为某个已知的概率分布，我们假定存在某随机变量 $ϵ\sim p_{ϵ}(ϵ)$，满足 $z=g_{\varphi }(ϵ,x)$，我们有 $\left|q_{\varphi }(z|x)dz\right|=\left|p_{ϵ}(ϵ)dϵ\right|$，因此，有下式
$$\begin{array}{rl}{▽}_{\varphi }\text{ELBO}& ={▽}_{\varphi }{\int }_z{q}_{\varphi }(z|x)\log \frac{p(x,z)}{q_{\varphi }(z|x)}dz\\ & ={▽}_{\varphi }{\int }_z\log \frac{p(x,z)}{q_{\varphi }(z|x)}{p}_{ϵ}(ϵ)dϵ\\ & ={\int }_z{▽}_{\varphi }\log \frac{p(x,z)}{q_{\varphi }(z|x)}{p}_{ϵ}(ϵ)dϵ\\ & ={\mathbb{E}}_{ϵ\sim p_{ϵ}}[{▽}_{\varphi }\log \frac{p(x,z)}{q_{\varphi }(z|x)}]\\ & ={\mathbb{E}}_{ϵ\sim p_{ϵ}}[{▽}_z\log \frac{p(x,z)}{q_{\varphi }(z|x)}{▽}_{\varphi }{g}_{\varphi }(ϵ,x)]\end{array}$$

变分自动编码器 (Variational AutoEncoder)

变分自编码器是变分推断与自编码器的一种组合，首先来简单介绍一下自编码器，经验可知，对于图像 $x\in {\mathbb{R}}^{H\times W\times 3}$ 等真实数据的高维数据，它们通常在空间中是稀疏分布的，大致分布在高维空间的某个流形上面，因此，我们希望将其投影到某个稠密分布的空间上，使其满足某些性质（例如，在该稠密空间上采样的任一一个点，投影回原始图像空间都能得到一个接近真实的图像），我们使用神经网络来执行不同表示空间的转换操作，如下所示

AE主要有encoder和decoder两个部分组成，其中encoder和decoder都是神经网络。其中encoder负责将高维输入转换为低维的隐变量，decoder负责将低维的隐变量转换为高维的图像输出，其中输出要跟输入尽可能的相似

通常情况下，网络的拟合能力要强于训练数据的多样性，假如 Autoencoders 中的 encoder 和 decoder 都具有无限的拟合能力，那么理论上我们就可以无损地把任何高维数据都压缩至维度为 1，无损的数据压缩往往会使得隐空间缺乏可解释性。在大多数情况下，空间转化不仅仅是为了降低数据维度，而是在降低数据维度的同时还能在隐空间中保留数据的主要结构信息。我们目前的损失函数只对每个样本点处进行约束，而并没有整个隐空间上给出约束信息，这使得该网络不能在样本点与样本点之间得到较好的插值结果

上图所示三种颜色表示三个样本点在隐空间上的位置，如果不引入额外的约束，只在样本点的某个小邻域内可以得到合理的图像结果，但大部分位置 Decoder 不能给出一个合理的图像生成结果。我们希望，对隐空间的样本点施加一个噪声的情况下，依旧约束 Decoder 重建出一张与原始图像相似的图片，整体流程如下所示

注意到对于上述流程中，采样这一步是无法进行反向传播的，采用重参数化技巧解耦 $z$ 的随机性和与参数 $\varphi$ 之间的关系。通常假定 $z|x\sim \mathcal{N}(\mu (x),{\sigma }^2(x)I)$，那么有
$$z=\mu (x)+\sigma (x)ϵ$$
其中 $ϵ\sim \mathcal{N}(0,I)$，网络结构如下所示

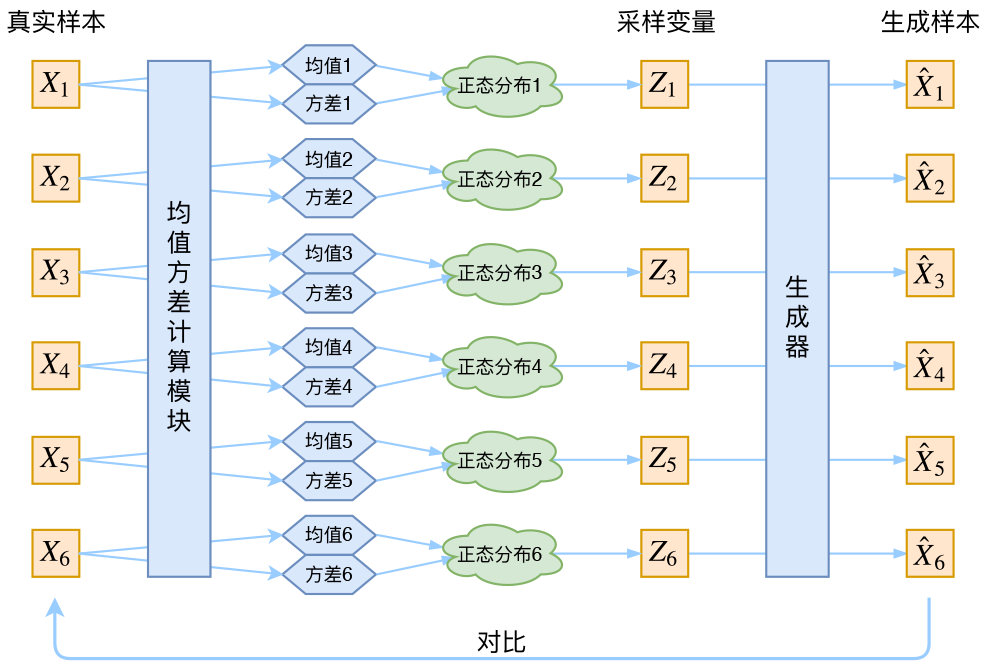
对于以上网络结构，显然噪声会增加重构的难度，其中噪声强度（方差）通过一个神经网络算出来的，如果不施加额外的约束，网络会倾向于让方差为0，模型会慢慢退化成普通的AutoEncoder，噪声不再起作用。

因此，为了避免模型退化，同时保证有意义的 $p(z)$ 分布（方便图像的生成任务），VAE让所有的 $p(z|x)$ 向标准正态分布看齐，如果所有的 $p(z|x)$ 都很接近标准正态分布 $\mathcal{N}(0,1)$，那么有
$$p(z)={\int }_{x}p(z|x)p(x)dx={\int }_x\mathcal{N}(0,1)p(x)dx=\mathcal{N}(0,1)$$
然后我们就可以从 $\mathcal{N}(0,1)$ 中采样来生成图像

约束项由 KL 散度给出，有如下结论：对于一维高斯分布 $p\sim \mathcal{N}({\mu }_1,{\sigma }_1^2)$ 和 $q\sim \mathcal{N}({\mu }_2,{\sigma }_2^2)$，满足
$$\text{KL}(p||q)=\log \frac{{\sigma }_2}{{\sigma }_1}+\frac{{\sigma }_1^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}$$
具体细节可见 高斯分布的KL散度，进一步，假定隐变量各维度是相互独立的，可以给出如下损失函数约束项（对于第 i 个分量）
$$\text{KL}(\mathcal{N}({\mu }^{(i)}(x),{\sigma }^{(i)}(x)),\mathcal{N}(0,1))=\frac{1}{2}({\mu }^{(i)}(x{)}^2+{\sigma }^{(i)}(x{)}^2-2\log {\sigma }^{(i)}(x)-1)$$

从数学角度来说，该优化问题可表示为
$$\begin{array}{rl}\hat{\theta },\hat{\varphi }& =\arg \underset{\theta ,\varphi }{\min }\text{KL}(q_{\varphi }(z|x)||p_{\theta }(z|x))\\ & =\arg \underset{\theta ,\varphi }{\max }\text{ELBO}\\ & =\arg \underset{\theta ,\varphi }{\max }{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]-\text{KL}(q_{\varphi }(z|x)||p_{\theta }(z|x))\end{array}$$

参考资料

白板推导机器学习