学习视频:
鲁鹏-计算机视觉与深度学习
同系列往期笔记:
【学习笔记】计算机视觉与深度学习(1.线性分类器)
【学习笔记】计算机视觉与深度学习(2.全连接神经网络)
【学习笔记】计算机视觉与深度学习(3.卷积与图像去噪/边缘提取/纹理表示)
【学习笔记】计算机视觉与深度学习(4.卷积神经网络)
1 AlexNet

AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的,将LeNet的思想发扬光大。该网络的精度相比2011年的冠军提升了超过10个百分点。
ImageNet大规模视觉识别挑战赛ILSVRC
- 计算机视觉领域最具权威的学术竞赛之一
- ImageNet数据集——由斯坦福大学李飞飞教授主导制作,其包含了超过1400万张全尺寸有标记图片
- ILSVRC从ImageNet数据集中抽出子集作为竞赛数据
2012年ILSVRC——1281167张训练集,50000张验证集,100000张测试集。
历年冠军
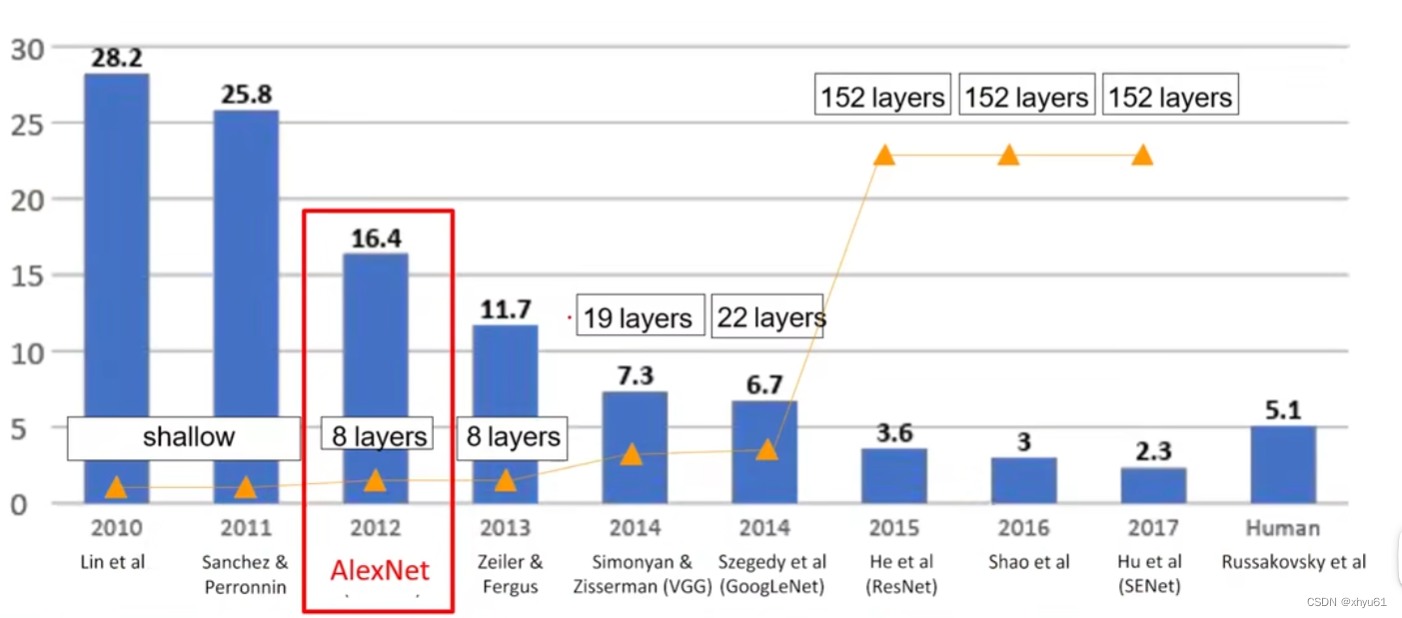
网络解析
AlexNet——验证了深度卷积神经网络的高效性
主体贡献:
- 提出了一种卷积层加全连接层的卷积神经网络结构
- 首次使用ReLU函数作为神经网络的激活函数
- 首次提出Dropout正则化来控制过拟合
- 使用加入动量的小批量下降算法加速了训练过程的收敛
- 使用数据增强策略极大地抑制了训练过程的过拟合
- 利用了GPU的并行计算能力,加速了网络的训练与推断
结构:

其中NORM为局部响应归一化层,现在已经不用了。
层数统计说明:
- 计算网络层数时仅统计卷积层与全连接层
- 池化层与各种归一化层都是对它们前面卷积层输出的特征图进行后处理,不单独算作一层。
不难看出,AlexNet是一个8层的网络(5层卷积层,3层全连接层)。
输入图像处理——去均值
假设给定图像尺寸为227×227×3227\times 227\times 3227×227×3,那么就分别求出所有样本中第iii个位置里所有数的均值μi\mu_iμi,然后把所有样本的该位置的每一个元素的数值减掉这个μi\mu_iμi。因为这个均值在我们的图像比较中没有任何意义,我们更在意其中的相对信息。
第1层 CONV1
96个11×1111\times 1111×11卷积核,步长为4,没有零填充。
问 输入227×227×3227\times 227\times 3227×227×3大小的图像,输出特征图个数及尺寸为多少?
答 特征图个数为969696(与卷积核个数相同),尺寸55×5555\times 5555×55。
问 该层有多少个参数?
答 (11×11×3+1)×96(11\times 11\times 3+1)\times 96(11×11×3+1)×96
综上:
- 第一个卷积层提取了96种结构的响应信息,得到了96个特征响应图。输出尺寸为55×55×9655\times 55\times 9655×55×96。
- 特征图每个元素经过ReLU函数操作后输出。
MAX POOL1
窗口大小3×33\times 33×3,步长为2。会发现我们每次的窗口存在重叠(重叠有助于对抗过拟合)。
作用:降低特征图尺寸,对抗轻微的目标偏移带来的影响。
特征图个数:969696
特征图尺寸:(55−3)/2+1=27(55-3)/2+1=27(55−3)/2+1=27,故为27×2727\times 2727×27
需要学习的参数个数:000
此层的输出规模为27×27×9627\times 27\times 9627×27×96。
NORM1
局部响应归一化层作用:
- 对局部神经元的活动创建竞争机制
- 响应比较大的值会变得更大
- 抑制其他反馈较小的神经元
- 增强模型泛化能力
后来的研究表明:更深的网络中该层对分类性能的提升效果并不明显,且会增加计算量与存储空间。
第2层 CONV2
256个5×55\times 55×5卷积核,步长为1,使用零填充p=2p=2p=2。
问 输入为27×27×9627\times 27\times 9627×27×96大小的特征图组,输出特征图个数及尺寸为多少?
答 特征图个数为256256256(与卷积核个数相同),尺寸27×2727\times 2727×27。
提升卷积核的个数,可以帮助捕获更多的特征。同时,相对于第一层卷积,我们每一个卷积核的尺寸小了,但是我们输入的图像也变小了,一个窗口感受到的图像区域变大了。
此层的输出规模为27×27×25627\times 27\times 25627×27×256。
MAX POOL2
采用和MAX POOL1相同的方式池化,输出规模变为13×13×25613\times 13\times 25613×13×256。
NORM2
第3/4层 CONV3/CONV4
两层结构相同:384个3×33\times 33×3卷积核,步长为1,使用零填充p=1p=1p=1。
问 CONV3时输入为13×13×25613\times 13\times 25613×13×256大小的特征图组,输出特征图个数及尺寸为多少?
答 特征图个数为384384384(与卷积核个数相同),尺寸13×1313\times 1313×13。
CONV3的输出规模为13×13×38413\times 13\times 38413×13×384。
第5层 CONV5
256个3×33\times 33×3卷积核,步长为1,使用零填充p=1p=1p=1。
MAX POOL3
通过最大池化层进一步缩小特征图尺寸。
第6~8层 FC6/FC7/FC8
全连接神经网络分类器。
MAX POOL3的输出是6×6×2566\times 6\times 2566×6×256的三维数据,我们通过逐个提取特征图按行提取数值的方式,将该三维数据拉平成一个6×6×256=92166\times 6\times 256=92166×6×256=9216维的向量,作为全连接神经网络的输入。
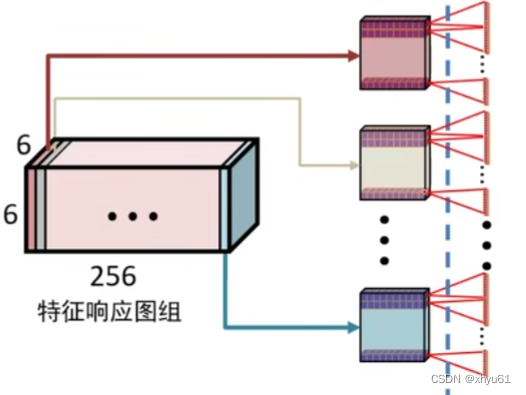
全连接神经网络的输出:图像类别概率
重要说明
- 用于提取图像特征的卷积层以及用于分类的全连接层是同时学习的
- 卷积层与全连接层在学习过程中会相互影响,相互促进
重要技巧
- Dropout策略防止过拟合
- 使用加入动量的随机梯度下降算法,加速收敛
- 验证集损失不下降时,手动降低10倍的学习率
- 采用样本增强策略增加训练样本数量,防止过拟合
- 集成多个模型,进一步提高精度
跨GPU计算

- AlexNet分布于两个GPU,每个GPU各有一半的神经元
- CONV1、CONV2、CONV4、CONV5仅使用在同一GPU的前层网络输出的特征图作为输入
- CONV3、FC6、FC7、FC8拼接前一层所有特征图,实现了神经网络的跨GPU计算
(但随着硬件的发展,今天我们已经不再使用这种策略)
卷积层到底在做什么?

2 ZFNet
与AlexNet网络结构基本一致!
主要改进:
- 将CONV1中的大小改为了7×77\times 77×7(将卷积核大小变小,关注更细节的东西)
- 将CONV1的卷积步长设置为2(减缓分辨率的下降)
- 增加了CONV3、CONV4的卷积核个数(增强分类能力)
3 VGG
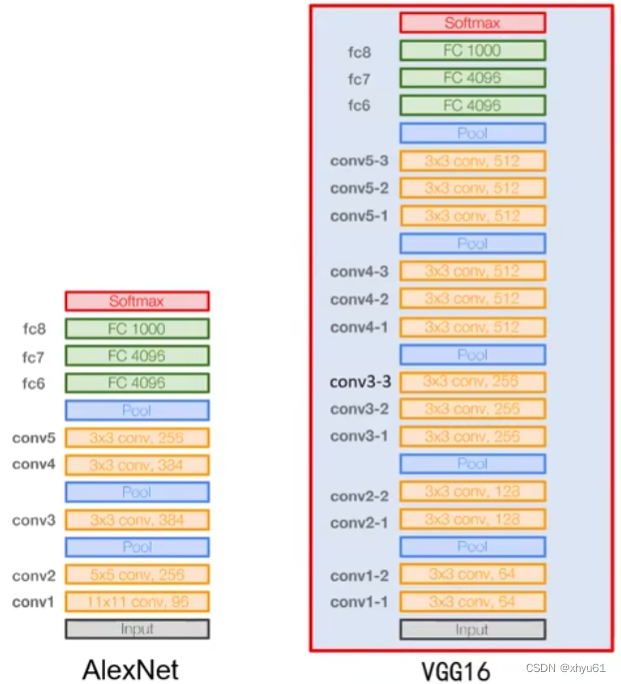
VGG网络贡献
- 使用尺寸更小的3×33\times 33×3卷积核串联来获得更大的感受野
- 放弃使用11×1111\times 1111×11和5×55\times 55×5的大尺寸卷积核
- 深度更深、非线性更强,网络的参数也更少(非线性更强,描述能力也会有所提升)
- 去掉了AlexNet中的局部响应归一化层。
网络分析
输入图像处理——与AlexNet的区别
AlexNet是针对图像的每一个位置计算一个均值,然后把每一个样本的这个位置的数值减去一个均值(RGB分别求,分别减)。VGG认为这很麻烦,所以不再考虑位置,而是把所有位置的R、G、B分别求一个均值μR,μG,μB\mu_R,\mu_G,\mu_BμR,μG,μB,然后把所有样本中每一个位置的像素点的RGB值分别减掉μR,μG,μB\mu_R,\mu_G,\mu_BμR,μG,μB。
简单特性
不难发现,VGG中,每一轮卷积均为连续进行多次想通规模的卷积,并且在每一轮卷积后都紧跟了一轮池化。
VGG16 vs VGG19
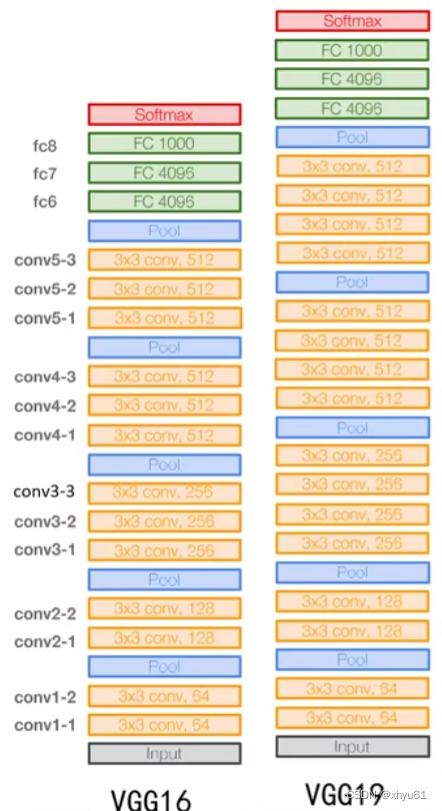
VGG19更深、精度略微,但所需的内存更多,所以通常我们更多使用的还是VGG16。
VGG16
- 由13个卷积层和3个全连接层组成,是一个16层网络
- 13个卷积层被分为5段:CONV1、CONV2、CONV3、CONV4、CONV5,每一段中卷积层的卷积核个数均相同
- 所有卷积层均采用3×33\times 33×3的卷积核以及ReLU激活函数
- 池化层均采用最大池化,其窗口为2×22\times 22×2,步长为222
- 经过一次池化操作后,其后卷积层的卷积核个数就增加一倍,直至达到512(为什么前层个数少、后层个数多?因为我们让前层先去学习一些基元——点、线、变、圆斑一类的基础图形,这些基元的数量很有限,但由基元组成的语义是非常多的,所以先少后多。同时,由于前层时输入较大,如果卷积元个数过多会导致计算量过大,经过一系列池化后,输入量逐渐变小,于是可以增加卷积核个数)
- 全连接层也是用了Dropout策略
思考
问 小卷积核有哪些优势?
答 多个小尺寸卷积核串联可以得到与大尺寸卷积核相同的感受野,如两个3×33\times 33×3的卷积核串联可以感受到一个5×55\times 55×5的卷积核的效果。
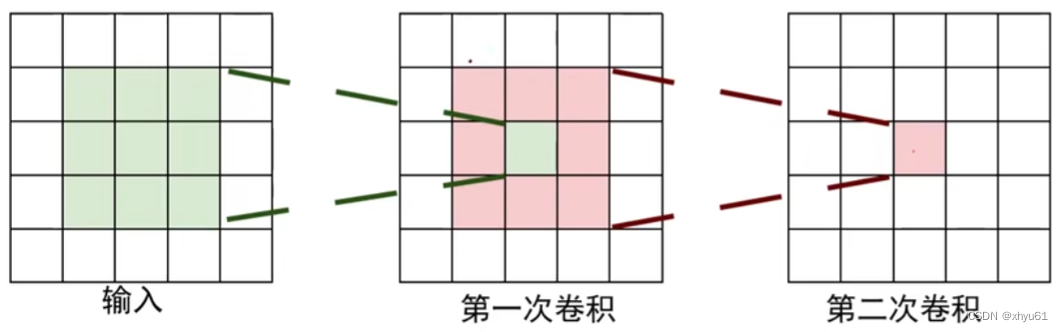
三个3×33\times 33×3,得到7×77\times 77×7的效果。
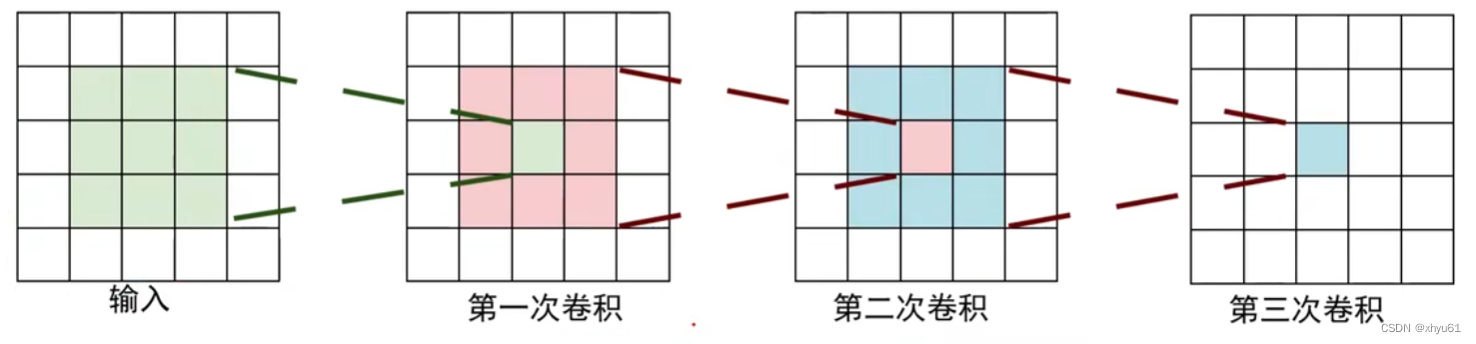
同时,使用小卷积串联构建的网络深度更深、非线性更强、参数也更少。
假设卷积层输入和输出的特征图数均为CCC,则:
- 三个3×33\times 33×3的卷积核串联时存储的参数个数为:
(3×3×C)×C×3=27C2(3\times 3\times C)\times C\times 3=27C^2(3×3×C)×C×3=27C2
(每一层输入的特征图数为CCC,所以当前层卷积核的层数也是CCC,故一个卷积核是3×3×C3\times 3\times C3×3×C个参数,由于我们要输出CCC个特征图,所以这一层我们也要准备CCC个这样的卷积核,所以在此基础上再×C\times C×C,由于我们串联了333个,所以在此基础上再×3\times 3×3) - 一个7×77\times 77×7的卷积核存储的参数个数为:
(7×7×C)×C=49C2(7\times 7\times C)\times C=49C^2(7×7×C)×C=49C2
不难看出,三个3×33\times 33×3的卷积核串联,需要存储的参数个数更少。
问 为什么VGG网络前四段里,每经过一次池化操作,卷积核个数就增加一倍?
答
- 池化操作可以减小特征图尺寸,降低显存占用
- 增加卷积核个数有助于学习更多的结构特征,但会增加网络参数数量以及内存消耗
- 一减一增的设计平衡了识别精度与存储、计算开销
最终有效提升了网络性能!
问 为什么卷积核个数增加到512个后就不再增加了?
答
- 第一层全连接层含102M参数,占总参数个数的74%(VGG最后进到FC前的参数规模为7×7×5127\times 7\times 5127×7×512,构成向量后维数很大)
- 这一层的参数个数是特征图的尺寸与个数的乘积
- 参数过多容易过拟合,且不易被训练
VGG证明的结论
- 将模型加深有助于学习结果的优化
- 小卷积核足以解决所有问题
- 归一化层效果不明显
4 GoogleNet
创新点
- 提出了一种Inception结构,它能保留输入信号中的更多特征信息
- 去掉了AlexNet的前两个全连接层,并采用了平均池化,这一设计使得GoogleNet只有500万参数,比AlexNet少了12倍
- 在网络的中部引入了辅助分类器,克服了训练过程中的梯度消失问题
串联结构存在的问题
后面的卷积层只能处理前层输出的特征图,前层因某些原因(比如感受野限制)丢失重要信息,后层无法找回。
解决方案:每一层尽量多的保留输入信号中的信息
Inception模块
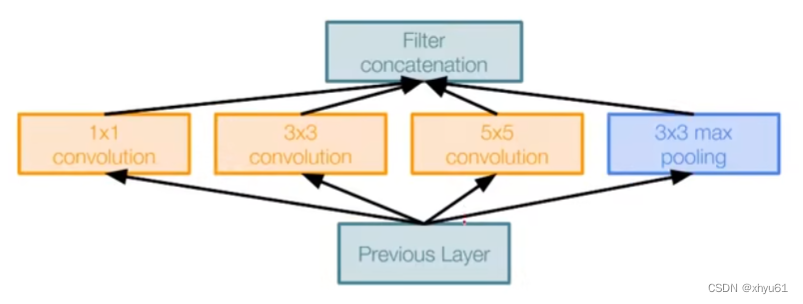
1×11\times 11×1的卷积层用于保留原图信息;3×33\times 33×3和5×55\times 55×5的卷积层用于提取不同感受野上的特征信息;3×33\times 33×3最大池化用于进行非最小化抑制。
需要控制卷积层内的卷积核大小或其他参数保证四个层的输出尺寸相同,才能将结果叠加到一起形成新的结果。
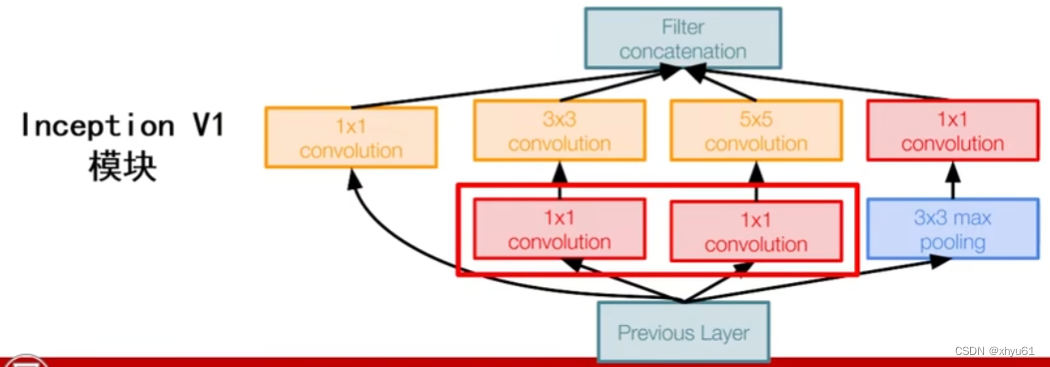
原模块的效率过慢,因此有了上图的改进。通过插入1×11\times 11×1的卷积层,控制其中的卷积核个数可以有效降低3×33\times 33×3和5×55\times 55×5的卷积层的运算速度(改变了这两层的输入参数规模)
层数更深,参数更少,计算效率更高,非线性表达能力也更强。
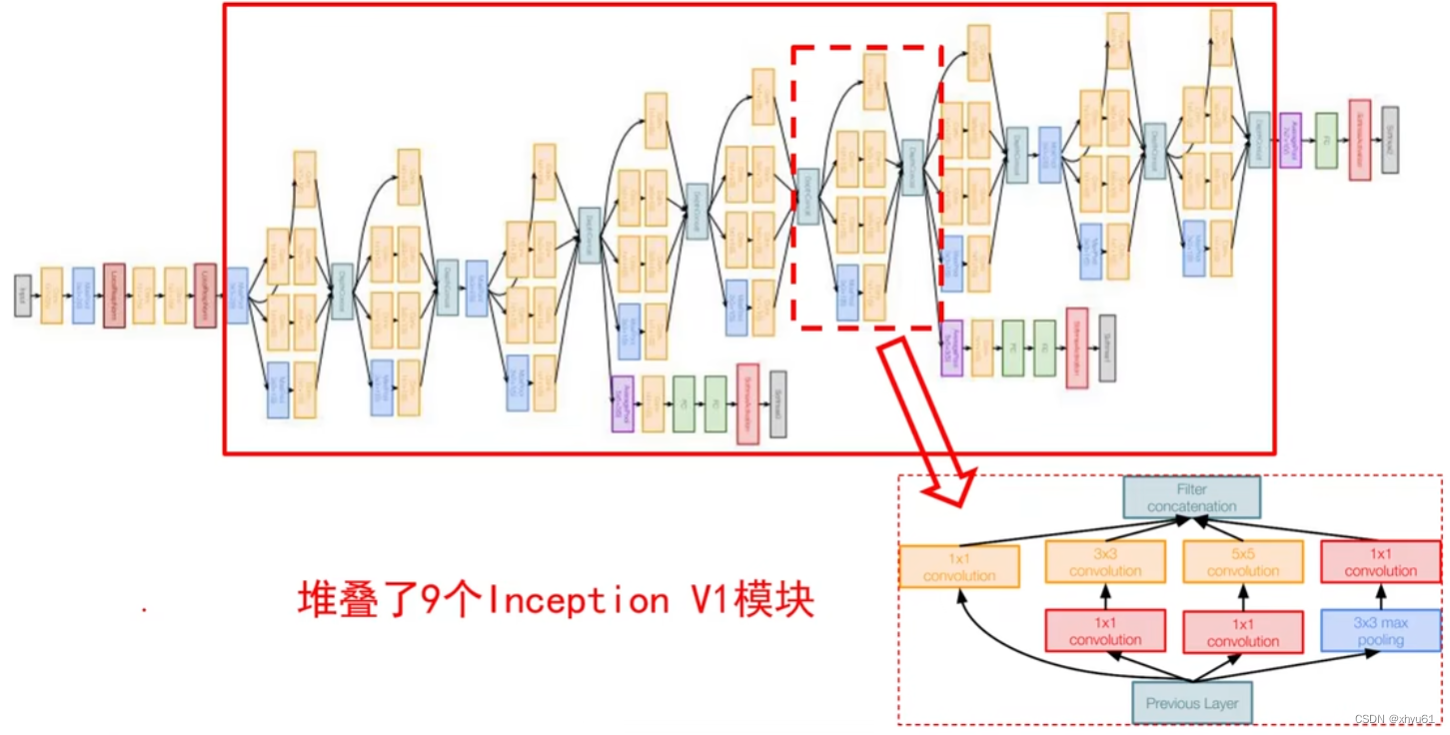
输入通过减RGB均值的方式处理;
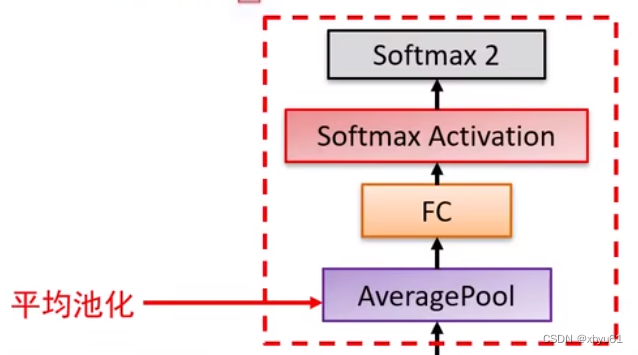
问 平均池化向量化和直接展开向量化有什么区别?
答 特征响应图上每一个位置的值反映了图像对应位置的结构与卷积核记录的语义结构的相似程度,平均池化丢失了语义结构的空间位置信息。忽略语义结构中的位置信息,有助于提升卷积层提取到的特征的平移不变性。
VGG的第一个全连接层参数占了整个网络的74%,需要dropout策略应对过拟合;
GoogleNet采用平均池化;
GoogleNet的参数总量不到500万,无需使用Dropout策略。
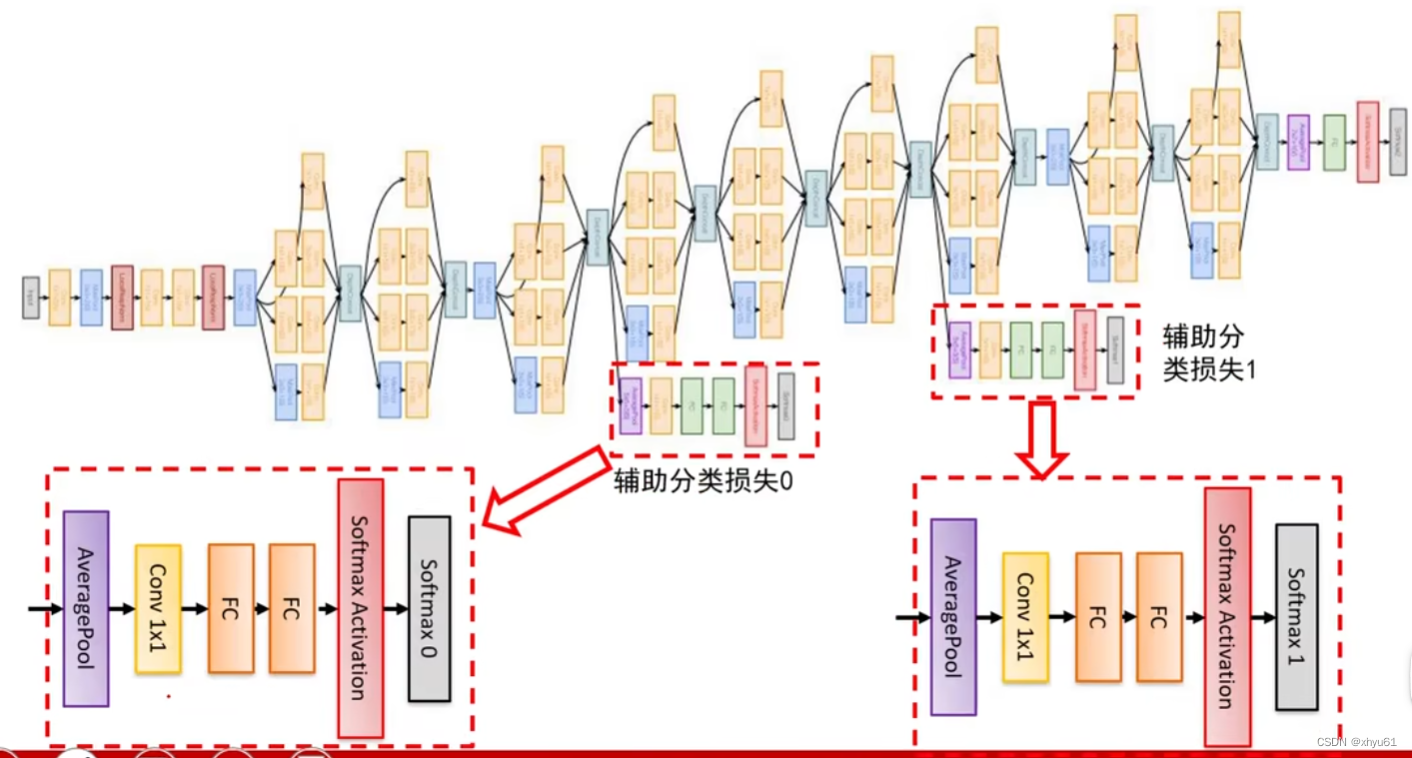
通过辅助分类损失部分可以有效解决梯度回传中存在的问题。
原因:
虽然ReLU单元能够一定程度上解决梯度消失问题,但是并不能解决深度网络难以训练的问题。离输出远的层就不如靠近输出的层训练得好。
结果:
让低层的卷积层学习到的特征也有很好的区分能力,从而让网络更好地被训练,而且低层的卷积层学到了好的特征也能加速整个网络的收敛。
网络推断:
仅利用网络最后的输出作为预测结果,忽略辅助分类器的输出。
问 利用1×11\times 11×1卷积进行压缩会损失信息吗?
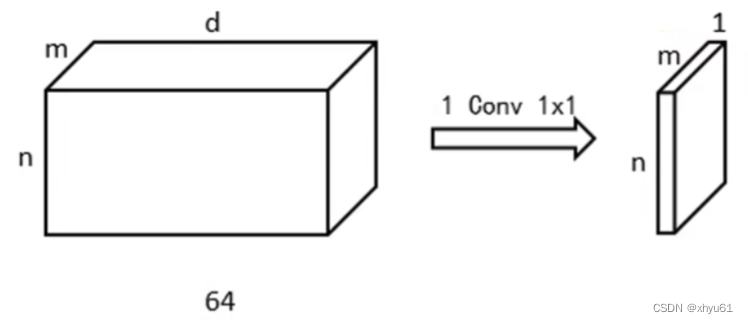
根据卷积方式不难发现,1×1×d1\times 1\times d1×1×d的卷积核并不会改变空间尺寸,对于图中n×m×dn\times m\times dn×m×d的特征图组,我们使用xxx个1×11\times 11×1的卷积核,就可以得到n×m×xn\times m\times xn×m×x的新的特征图组。通常我们选取x<dx<dx<d以实现空间压缩。
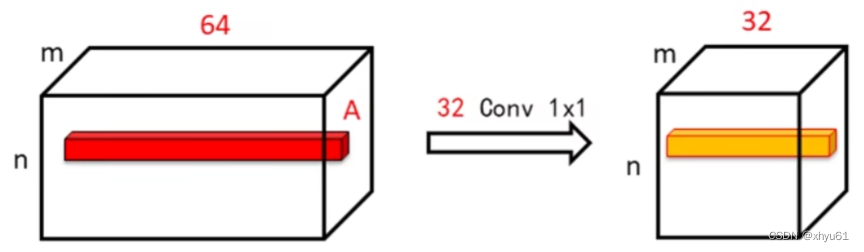
相当于如上图所示,把红色的长向量变成黄色的短向量。不论是红色的长向量还是黄色的短向量,他们都是在描述原输入图像中某一个位置上的特征信息,用646464种卷积核对这个位置的点进行比对得到646464种结果,但是同一个位置的点不会包含这么多特征,有绝大部分特征在这个点上是不匹配的,所以我们得到的646464维结果向量也会很稀疏。稀疏矩阵的压缩不会损失多少信息。绝大多数的点都只会响应至多一个向量。
5 ResNet
实验:持续向一个“基础”的卷积神经网络上面叠加更深的层数会发生什么?
在之前的几个网络中我们发现加深了神经网络层数对我们的准确率提高有帮助,这个结论真的是对的嘛?
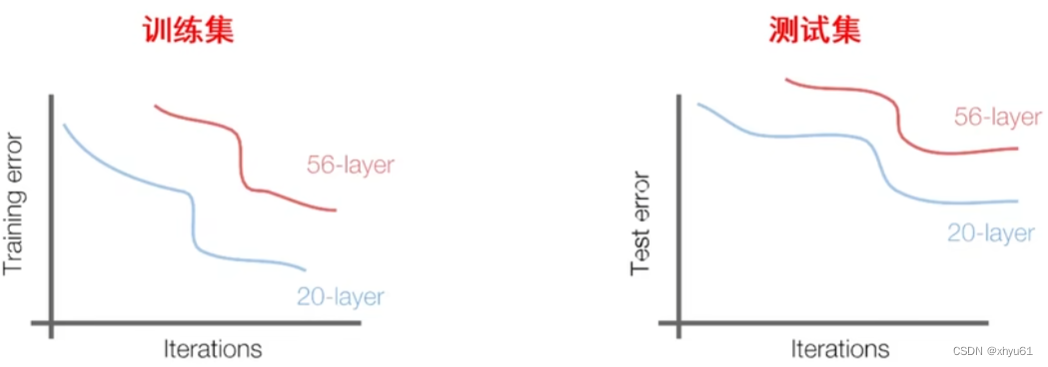
测试集上56层比20层的错误率高,猜测:加深网络层数引起过拟合,导致错误率上升。
但我们在训练集上也出现了这种56层比20层高的情况。原因是训练过程中网络的正、反向信息流动不顺畅,网络没有被充分训练。
模型的贡献
- 提出了一种残差模块,通过堆叠残差模块可以构建任意深度的神经网络,而不会出现“退化”的现象。
- 提出了批归一化方法(减均值去方差)来对抗梯度消失,该方法降低了网络训练过程对于权重初始化的依赖。
- 提出了一种针对ReLU激活函数的初始化方法。(即He初始化)
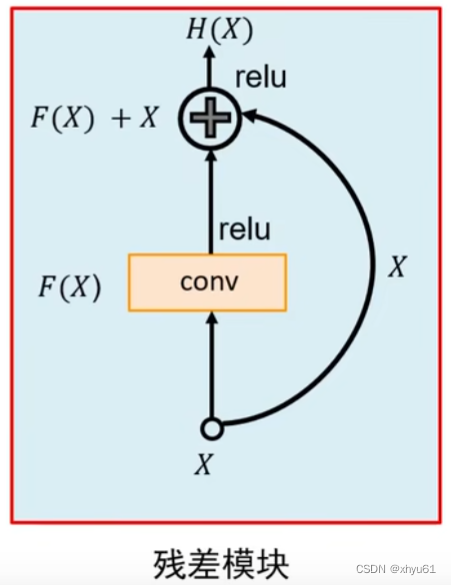
残差模块
研究者考虑了这样的问题:
浅层网络学习到了有效的分类模式后,如何向上堆积新层来建立更深的网络,使其满足即使不能提升浅层网络的性能,深层网络也不应降低性能。(后面的神经元层,即使不干好事,也别干坏事)
解决方案:残差模块
假设卷积层学习的变换为F(X)F(X)F(X),残差结构的输出是H(X)H(X)H(X),则有:
H(X)=F(X)+XH(X)=F(X)+XH(X)=F(X)+X
即哪怕F(X)F(X)F(X)没有得到好结果,被激活后,也至少会有H(X)=XH(X)=XH(X)=X。
考虑反向传递梯度:如果没有+X+X+X,那么此处根据链式法则直接从H(X)H(X)H(X)处乘上一个∂F(X)∂X\frac{\partial F(X)}{\partial X}∂X∂F(X),这个东西可能会变成000,从而导致梯度消失问题。但由于我们有一条支路XXX,在残差模块开始位置接收到的梯度永远是来自卷积层的梯度和来自XXX的梯度之和,不难发现此处的梯度永远是∂F(X)∂X+1\frac{\partial F(X)}{\partial X}+1∂X∂F(X)+1,这使得梯度消失永远不会发生。
F(X)=H(X)−XF(X)=H(X)-XF(X)=H(X)−X
其中F(X)F(X)F(X)表示残差,H(X)H(X)H(X)表示输出,XXX表示输入,于是我们有残差=输出-输入。
关于残差结构:
- 残差结构能够避免普通的卷积层堆叠存在信息丢失问题,保证前向信息流的顺畅。
- 残差结构能够应对梯度反传过程中的梯度消失问题,保证反向梯度流的通顺。
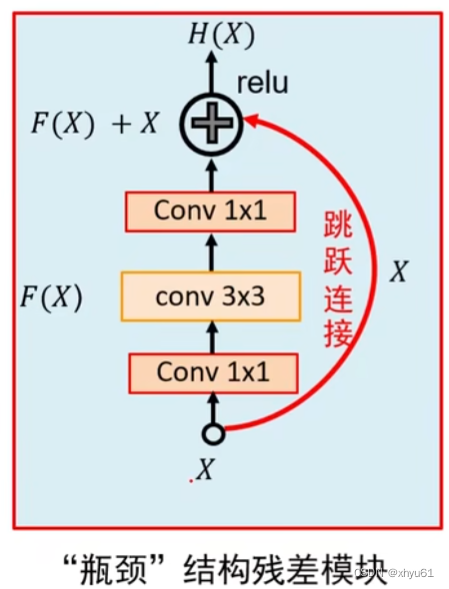
在"CONV 3×3"前后加两个"CONV 1×1",目的是降低计算量。第一个"CONV 1×1"可以先使用少量卷积核,降低特征图组的深度,但不改变尺寸,然后经过"CONV 3×3"后再用一个"CONV 1×1"把深度搞回来,回复到原来的程度。
网络结构
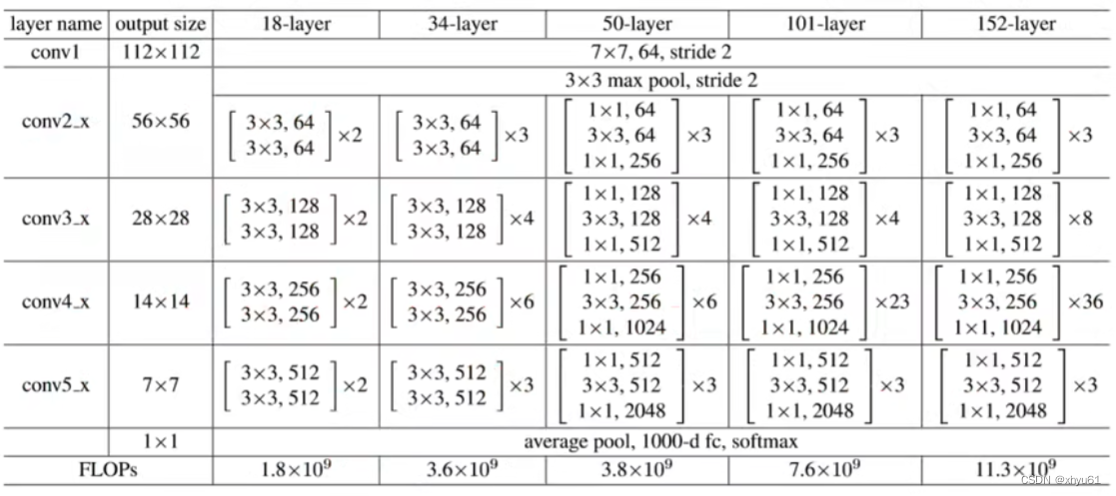
其他关键点:
- 提出了批归一化策略,降低了网络训练过程对于权重初始化的依赖
- 提出了针对ReLU非线性单元的初始化方法
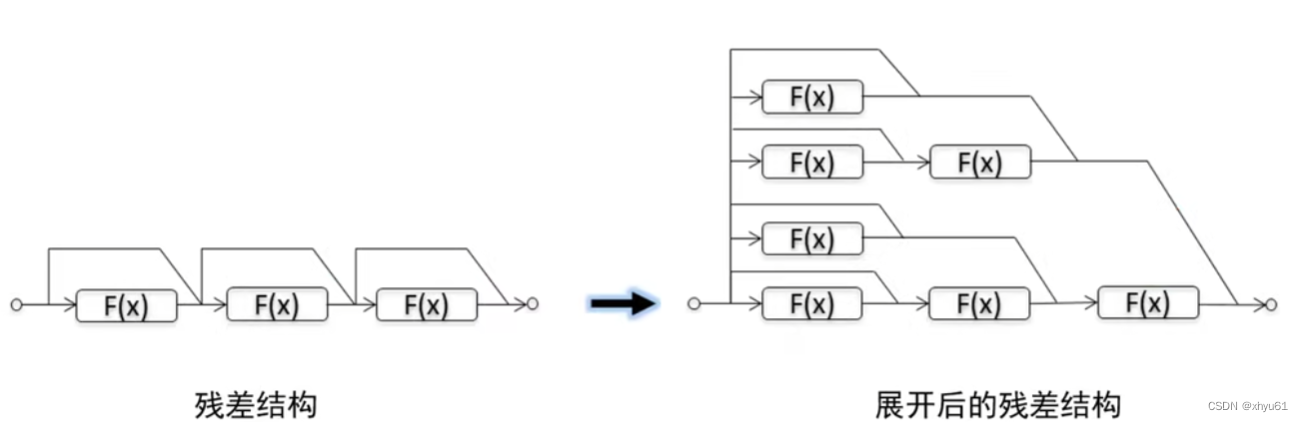
问 为什么残差网络的性能这么好?
答 一种典型的解释:残差网络可以看做是一种集成模型。它可以被看做是很多子网络的求和。同时这种结构有利于应对异常情况,当其中一层残差结构出现状况导致不能工作时,有其他残差结构组成的集成模型依旧可以很好地工作。
6 小结
- 介绍了5种经典的卷积神经网络AlexNet、ZFNet、VGG、GoogleNet、R额是Net
- 残差网络和Inception V4是公认的推广性能最好的两个分类模型
- 特殊应用环境下的模型:面向有限存储资源的SqueezeNet以及面向有限计算资源的MobileNet和ShuffleNet