题目链接: https://leetcode.com/problems/largest-divisible-subset/

Given a set of distinct positive integers, find the largest subset such that every pair (Si, Sj) of elements in this subset satisfies: Si % Sj = 0.

If there are multiple solutions, return any subset is fine.

Example 1:

nums: [1,2,3]Result: [1,2] (of course, [1,3] will also be ok)

Example 2:

nums: [1,2,4,8]Result: [1,2,4,8]

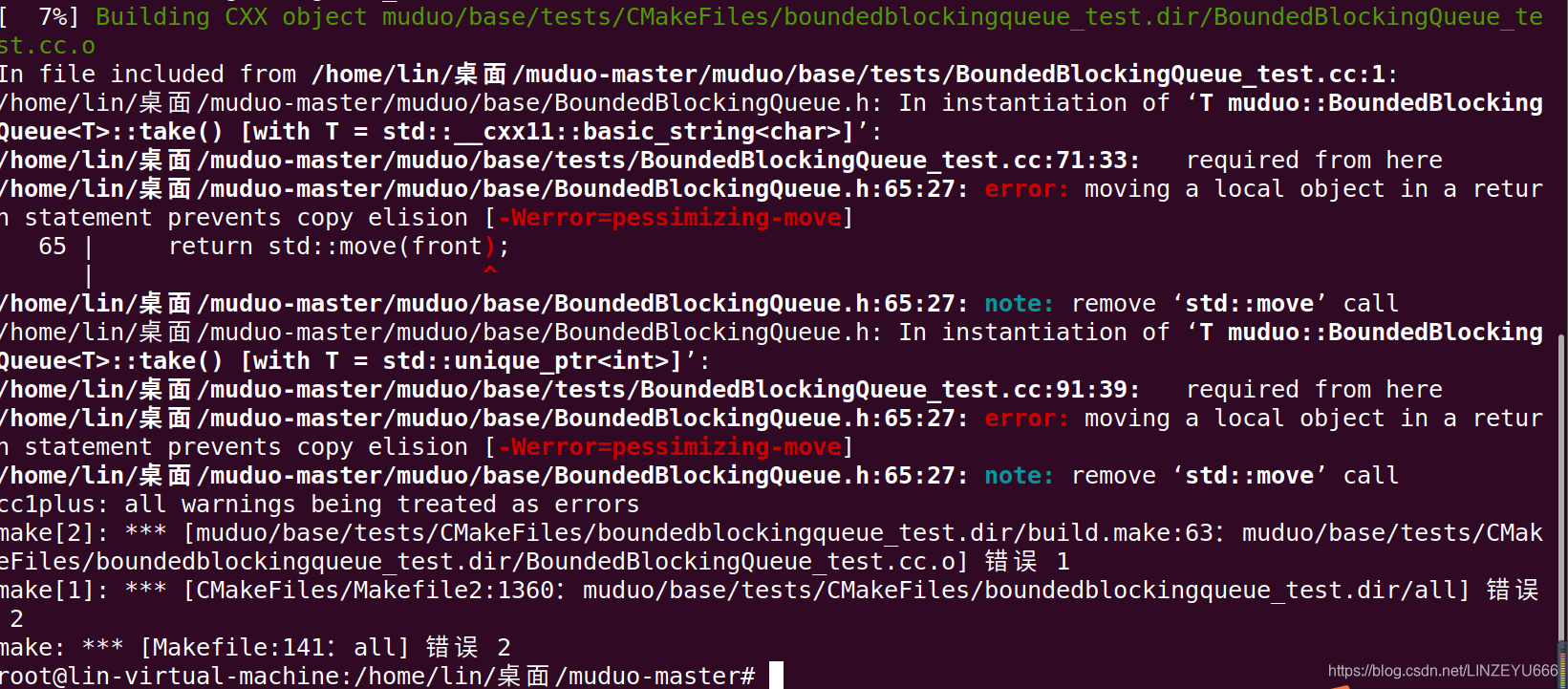
思路: 可以用动态规划来解决. 为了使得问题可以转化为子问题, 最好将数组按照降序来排列, 然后当nums[j]%nums[i]==0的时候就可以得到一个状态转移方程dp[i] = max(dp[i], dp[j]+1), 因为数组按照降序排序, 所以nums[i] < nums[j],并且之前能够被nums[j]整除的数, 也必然能够别nums[i]整除, 这就保证了状态转移方程的正确性. 

他还要求找出最大结果, 所以我们还需要记录一下路径, 每一个数字, 我们记录一个第一个能够使其到达最大长度的父结点, 最后回溯一下即可.

代码如下:

class Solution {
public:vector<int> largestDivisibleSubset(vector<int>& nums) {if(nums.size() ==0) return {}; sort(nums.begin(), nums.end(), greater<int>());int len = nums.size(), curMax=1, k=0;vector<int> par(len), dp(len, 1), result;for(int i =0; i < len; i++) par[i] = i;for(int i =1; i < len; i++){for(int j =0; j < i; j++){if(nums[j]%nums[i]!=0) continue;if(dp[i] < dp[j]+1) par[i] = j, dp[i]=dp[j]+1;if(dp[i] > curMax) curMax = dp[i], k = i;}}while(par[k] != k){result.push_back(nums[k]);k = par[k];}result.push_back(nums[k]);return result;}
};