---

前言

堆排序是一种非常高效的排序算法，它可以在O(n log n)的时间内对任意序列进行排序。它的原理是利用数据结构，堆的性质，将序列构建成一个大根堆或小根堆，然后不断地交换堆顶元素和最后一个元素，并调整堆的结构，直到堆为空。

如果你对数据结构，堆还不太熟悉，或者你想复习一下它的基本概念和操作，请先阅读我之前写的一篇文章【数据结构】堆，你可以在我的博客中找到它。如果你已经掌握了数据结构，堆的知识，那么请继续阅读这篇文章，我将为你详细地介绍算法，堆排序的过程和代码实现。如果你觉得这篇文章对你有帮助，或者你想了解更多关于数据结构和算法的知识，请给我点赞👍，并关注我的博客。我会不定期地分享更多有趣和实用的内容。谢谢你的阅读和支持！

---

堆排序的介绍

1.1 堆排序是什么

堆排序指的是将一组数据看成堆，再对其进行排序。
分为两个过程

1. 建堆：将数据排成大根堆或小根堆，用于找最大/最小
2. 排序：将数据排成升序或降序

其中它们涉及核心函数为

• 向上调整函数AdjustUp()
• 向下调整函数AdjustDown()

1.2 为什么使用堆排序

因为时间复杂度小。
建堆的时间复杂度最小为O(n)
排序的时间复杂度最小为O(n*long(n)) 这比之前学习的冒泡排序要更好

---

下面，我将为你介绍如何设计堆排序，以及如何计算它的时间复杂度。

二、建堆

建堆分为2种，向上调整建堆和向下调整建堆，其中向下调整建堆的时间复杂度更优，向上调整建堆更容易理解。

建堆可以用来找最大/最小值。现在给一个一维数组a,共十个元素，均为int类型，无序。

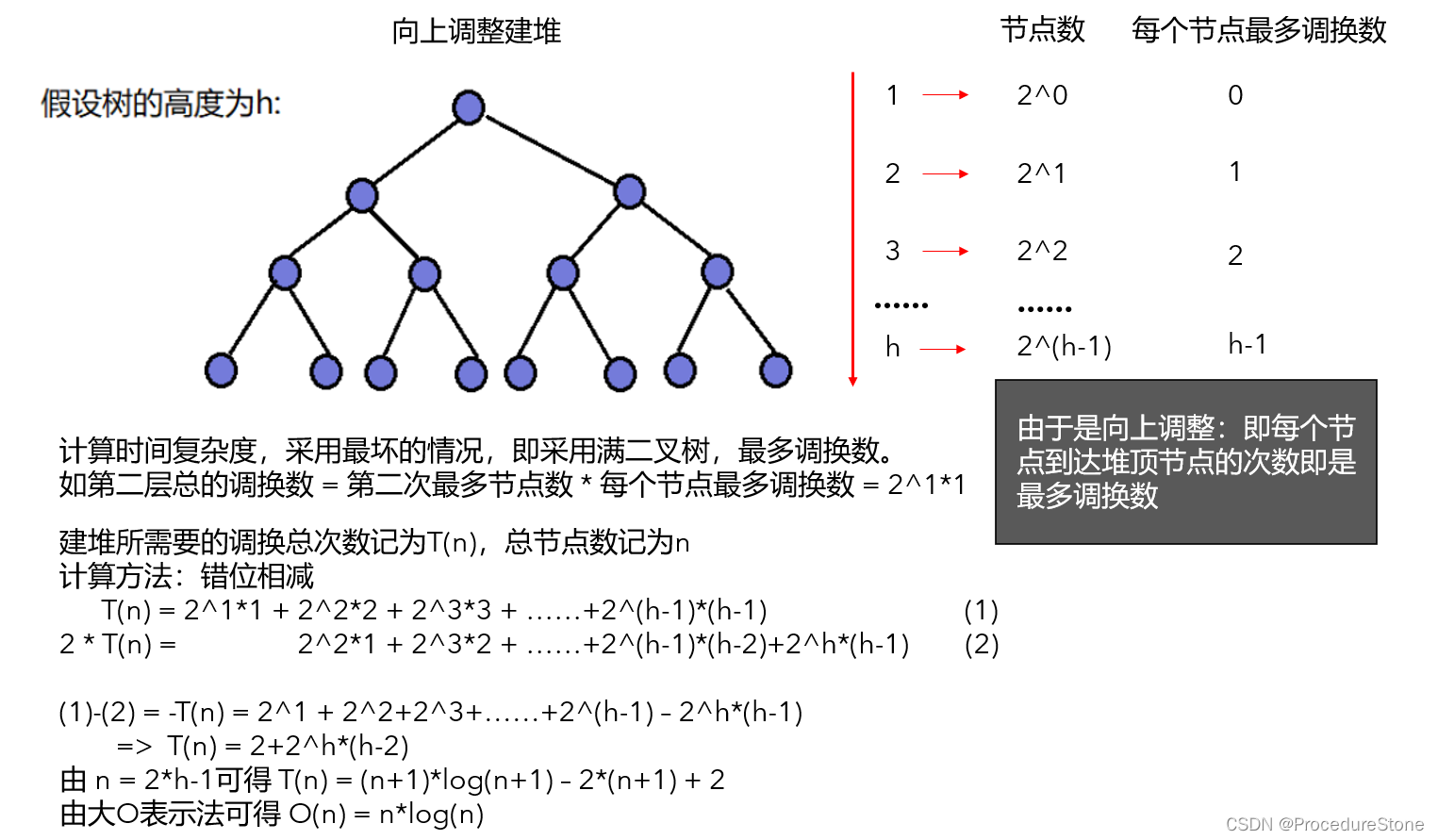
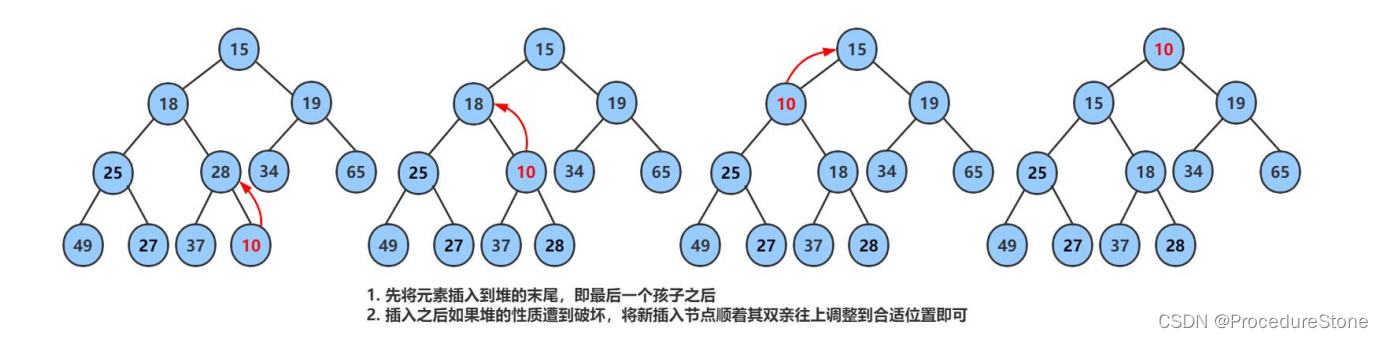
2.1 向上调整建堆 - O(n*log(n))

向上调整建堆的核心：将a[0]之后的数据看成一次次插入进去。

这里建的是大堆

---

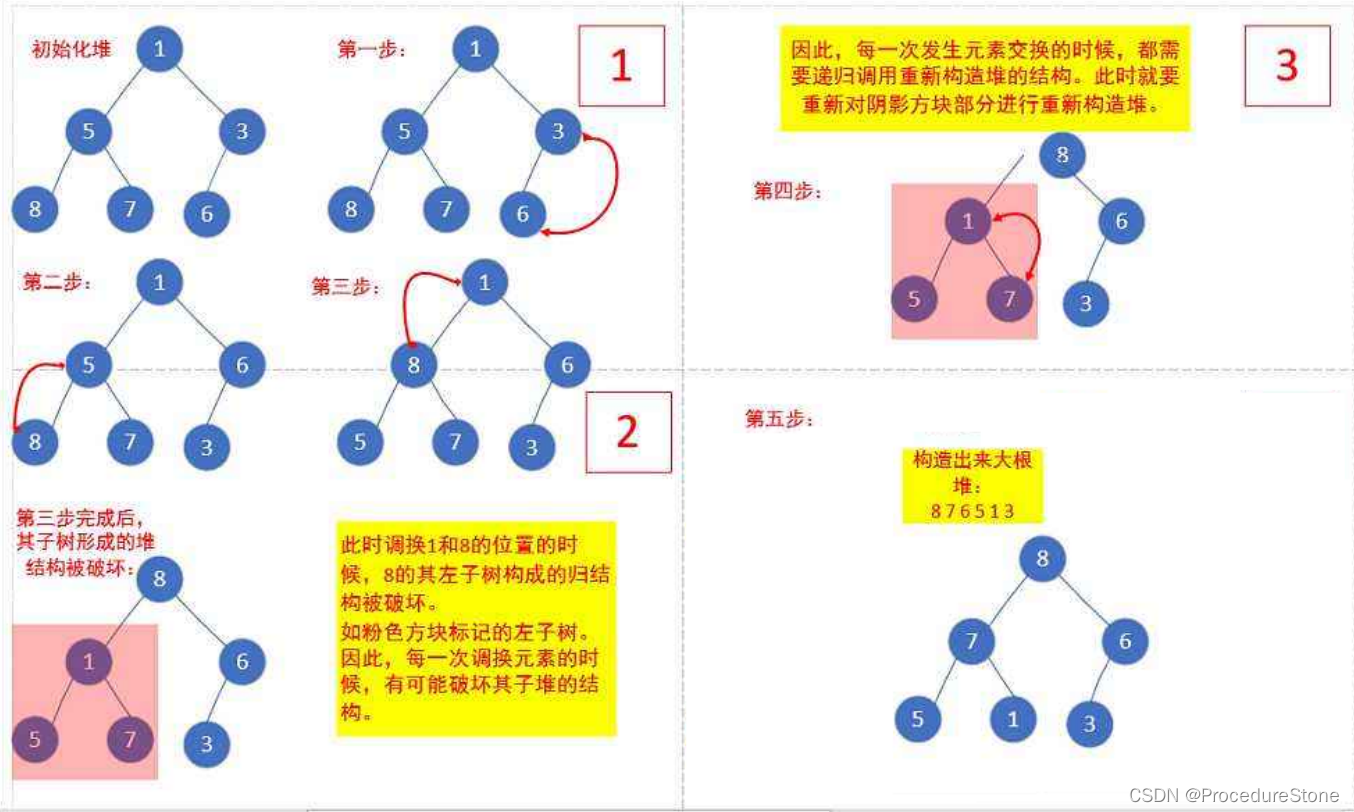
2.2 向下调整建堆 - O(n)

向下调整建堆：我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆。

---

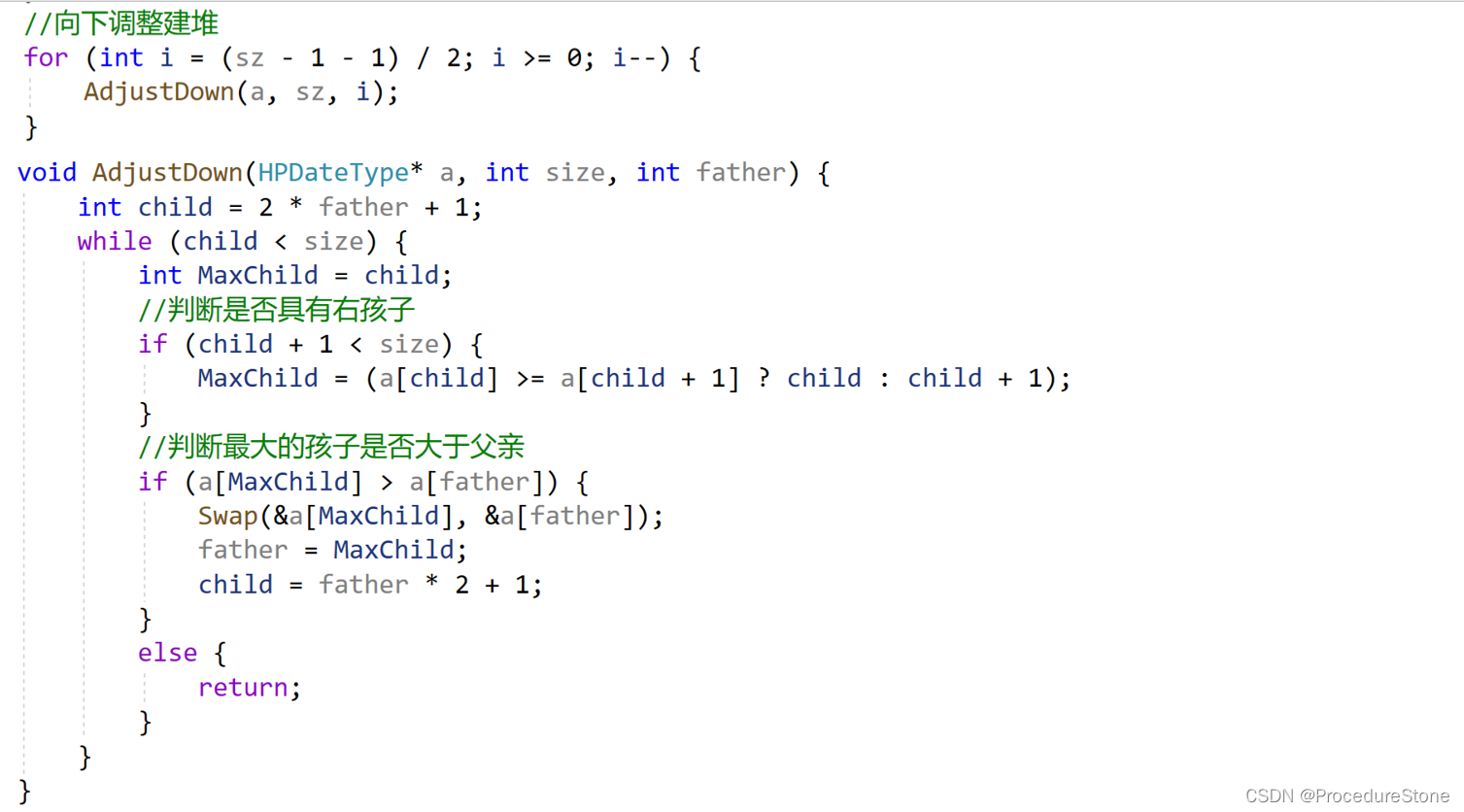
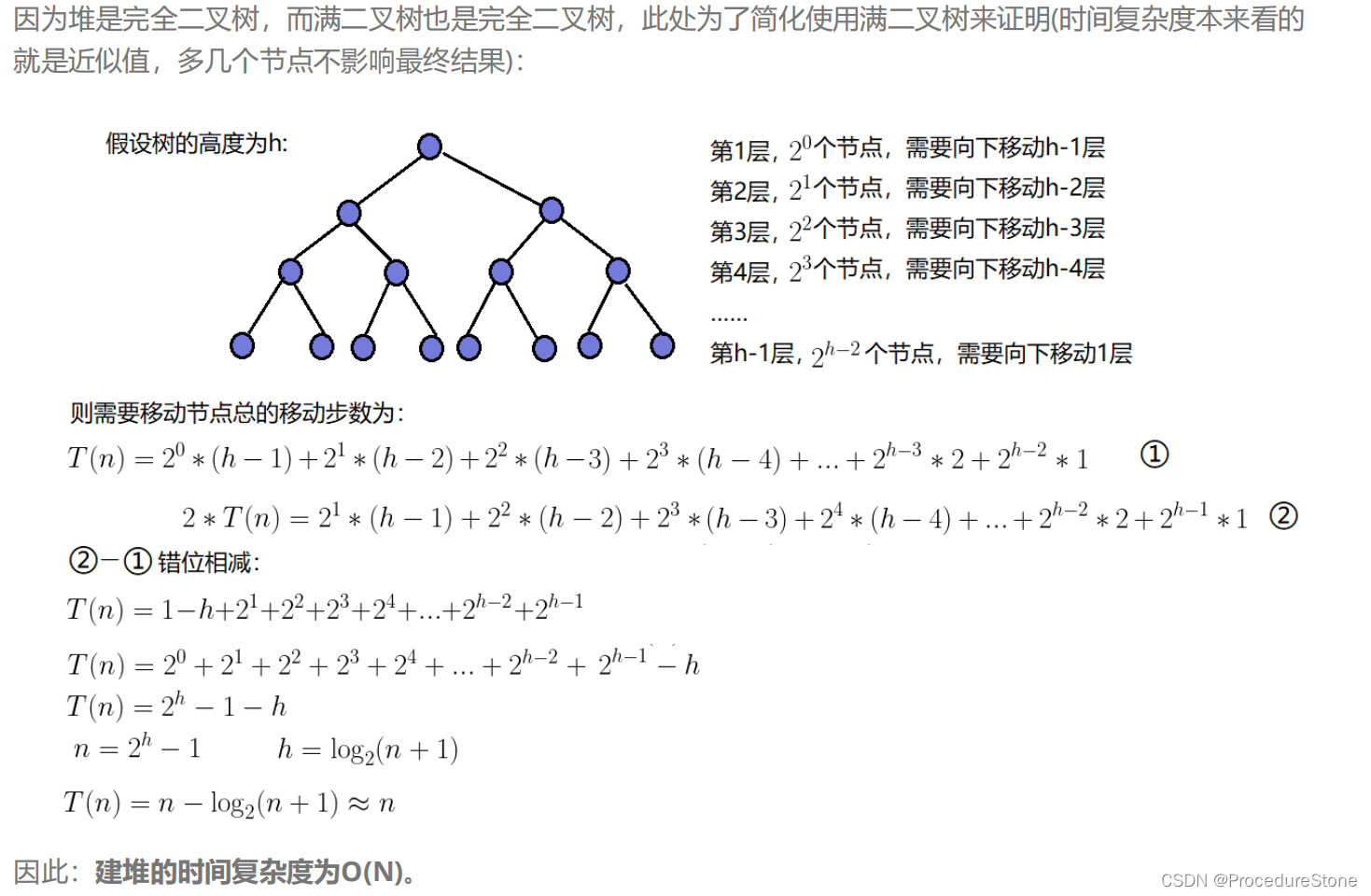
因为向下调整建堆的时间复杂度更小，所有一般采用向下调整建堆。

void HeapSort(int* a, int sz) {//建堆//向上调整建堆/*for (int i = 1; i < sz; i++) {AdjustUp(a, i);}*///向下调整建堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, sz, i);}
}

通过建堆便可以找出最大或最小值，但如果要进行拍成升序或降序则下面的排序算法。

---

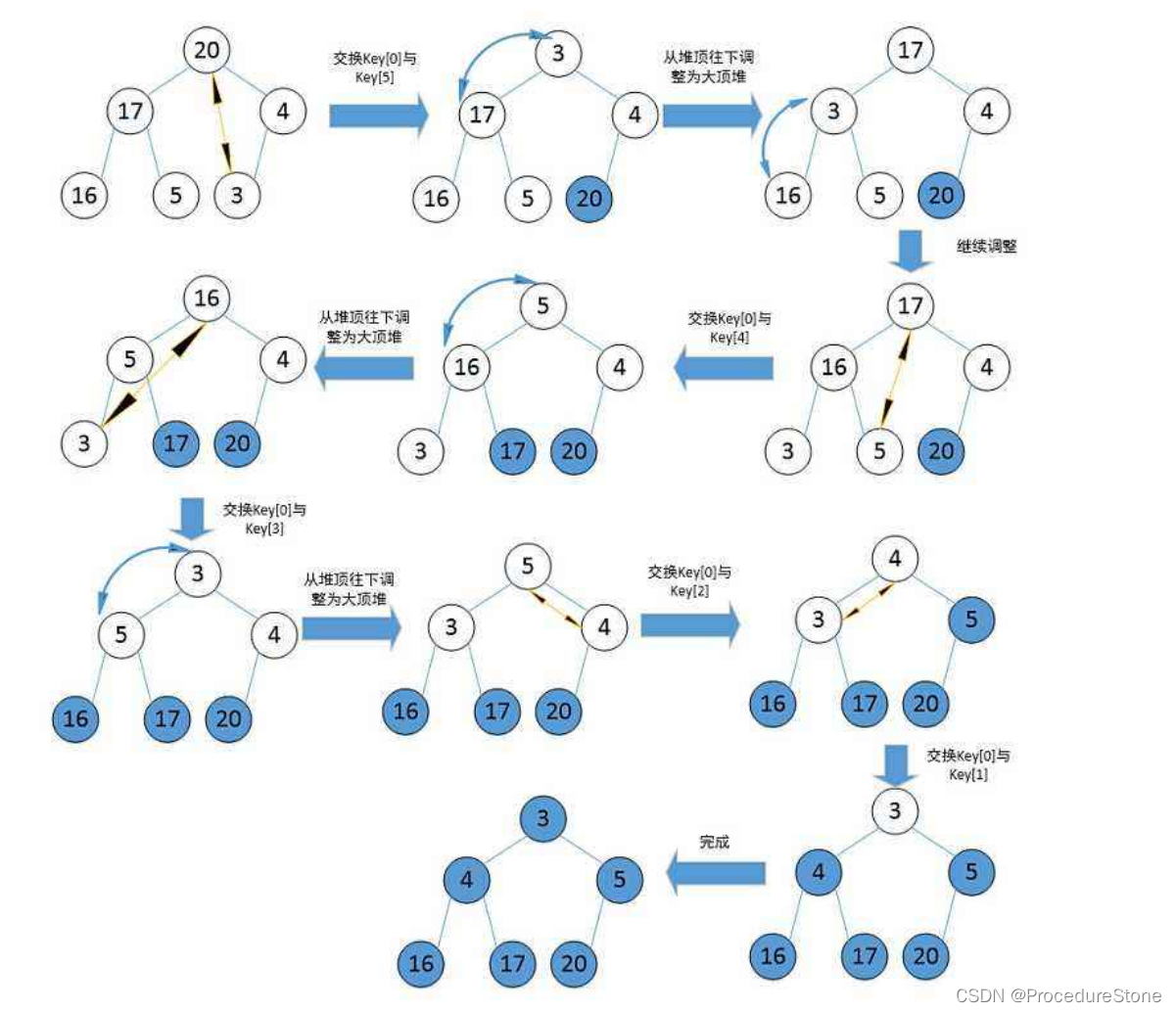
三、排序

现在我已经建好堆了，那该如何把数组a排成升序呢？

void HeapSort(int* a, int sz) {//向下调整建堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, sz, i);}//排序for (int j = 0; j < sz-1; j++) {Swap(&a[0], &a[sz - 1 - j]);AdjustDown(a, sz-j-1, 0);}
}

思想和堆的删除一样

• 先将堆顶元素与尾元素换位
• 再对首元素进行向下调整

注意：AdjustDown的第二个参数size.

---

总结

总之，堆排序是一个非常高效、稳定的排序算法，它在处理大规模数据时表现尤为出色。如果你能够理解并掌握它的实现原理，相信你在以后的程序开发中一定能事半功倍。希望这篇文章能够帮助到你，并且让你对堆排序有更深入的了解。如果你觉得这篇文章有帮助，不妨点个赞支持一下哦。谢谢大家的阅读！