112.路径总和

• 本题因为一些奇怪的原因卡了很久，注意复盘

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

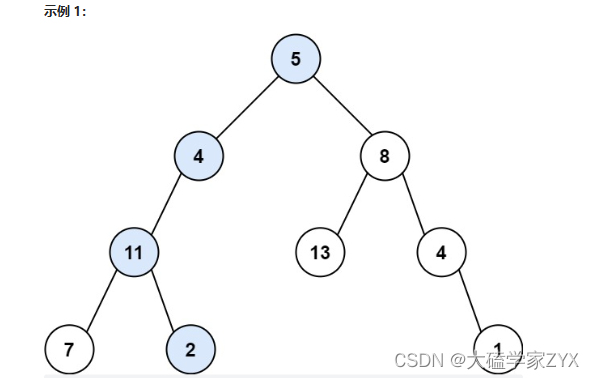
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

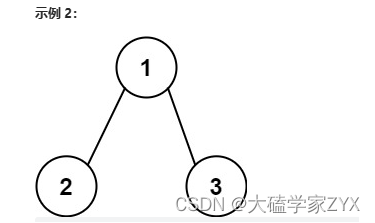
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

思路

这道题同样没有中的处理逻辑,我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。

对于递归的做法，前中后序都可以，因为没有中节点逻辑，只是左右子树一直计算节点值之和。

递归首先确定参数与返回值，此处的递归参数除了根节点之外，仍然有其他的参数，也就是传入的总和的数值。

伪代码

• 找到一条路径立刻返回，靠的就是返回值
• 从0开始累加再判断和目标和是否相等，比较麻烦，可以考虑用递减，以初始的target作为目标值，每一层减去节点val，如果遍历到了叶子节点并且target减到0，就可以返回true

bool travelsal(TreeNode* root,int target){//传入的参数也需要传计数器，累计每一条路径上节点的和  //从0开始逐渐累加比较麻烦，可以选择直接传入总和result，每到一个节点做减法操作//终止条件：叶子节点if(root->left==NULL&&root->right==NULL&&target==0){return true;}//单层递归：target--if(root->left){//本题目递归函数有返回值，需要对返回值进行处理判断bool result= travelsal(root->left,target-root->left->val);if(result){return true;}}if(root->right){bool result = travelsal(root->left,target-root->left->val);if(result){return true;}}return false;    
}

完整版写法1

class Solution {
public:bool travelsal(TreeNode* root,int target){//传入的参数也需要传计数器，累计每一条路径上节点的和  //从0开始逐渐累加比较麻烦，可以选择直接传入总和result，每到一个节点做减法操作//终止条件：叶子节点if(root->left==NULL&&root->right==NULL&&target==0){return true;}//单层递归：target--if(root->left){//本题目递归函数有返回值，需要对返回值进行处理判断bool result= travelsal(root->left,target-root->left->val);if(result){return true;}}if(root->right){//要注意如果左右子树逻辑相同，复制代码过来的时候一定要把所有的left都改成right，不能漏掉……bool result = travelsal(root->right,target-root->right->val);if(result){return true;}}//如果上面的情况都不满足，就return falsereturn false;    
}bool hasPathSum(TreeNode* root, int targetSum) {if(root==NULL){return false;}return travelsal(root,targetSum-root->val);}
};

写法1必须分开两个函数的原因

这种写法，需要把递归的部分单独拿出来，然后在主函数中传入travelsal(root,targetSum-root->val)，也就是说，需要在传入的时候就对根节点本身就是叶子节点的情况进行处理。

如果只写一个函数，那么，当二叉树只有一个叶子节点的时候，也就是输入[1]，sum=1的时候，输出是相反的。因为只写一个函数的话，没有处理二叉树根节点的root->val。

最开始只写一个函数的写法：

• 如果想要只写一个函数，应当参考写法2，在最开始就进行targetSum-root->val，然后左右子树的递归中，不再对targetSum进行数值处理。将写法1改写为只需要一个函数，那么它将与写法2变得非常相似。

class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {//传入的参数也需要传计数器，累计每一条路径上节点的和if(root==NULL){return false;}//从0开始逐渐累加比较麻烦，可以选择直接传入总和result，每到一个节点做减法操作bool result;//终止条件：叶子节点if(root->left==NULL&&root->right==NULL){if(targetSum==0){return true;}return false;}//单层递归：target--if(root->left){targetSum=targetSum-root->left->val;result = hasPathSum(root->left,targetSum);if(result){return true;}else{return false;}targetSum+=root->left->val;}if(root->right){targetSum = targetSum-root->right->val;result = hasPathSum(root->right,targetSum);if(result){return true;}else{return false;}targetSum += root->right->val;}return false;}
};

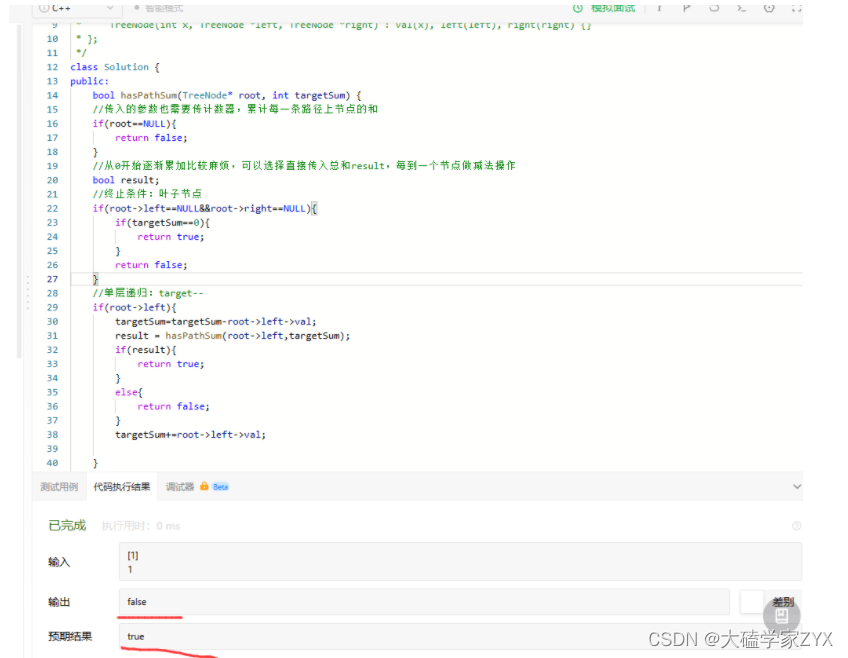
注意点

另一个注意点是，当左右子树逻辑相同的时候，如果要把左子树的代码复制粘贴到右子树，一定要把所有的left都改成right……因为这个问题卡bug了很久最后才发现，除此之外还有递归能直接返回就直接返回，有时候定义变量定义太多会给自己找麻烦。

完整版写法2

• 这道题也可以不采取回溯，直接采用前序遍历，中左右的方式，中的处理逻辑是targetSum自减，不涉及到回溯。更推荐这种写法，不需要考虑root->val传入的时候先自减的问题。
• 在最后直接return false，是因为前面所有的逻辑都会直接return，如果前面都没有return，就直接return false

class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {//bool result;//终止条件if(root==NULL){return false;}//中的处理逻辑targetSum -= root->val;// 遇到叶子节点，并且计数为0，返回trueif (!root->left && !root->right && targetSum == 0) {return true;}// 递归调用左子树和右子树,递归有返回值，直接接收返回值并判断if (hasPathSum(root->left, targetSum)){return true;}if (hasPathSum(root->right, targetSum)){return true;}//如果所有的情况都没有return,就return falsereturn false;}
};

写法2不涉及到回溯的原因

写法1里面，需要回溯的原因是在左子树内部的操作中，本层递归的targetSum发生了改变，那么在遍历右子树的时候，本层递归的targetSum必须恢复到遍历左子树之前的值，不然targetSum的值会出错。

但是，写法2中，直接在前序遍历处理逻辑中，对targetSum进行了操作，不涉及到左子树的内部操作，因此就不需要在遍历右子树的时候，恢复到遍历左子树之前的值。

• 能直接返回就直接返回，不要定义新的变量给自己找麻烦，比如写法2如果定义bool result的话，写法就麻烦很多

106.中序和后序遍历构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

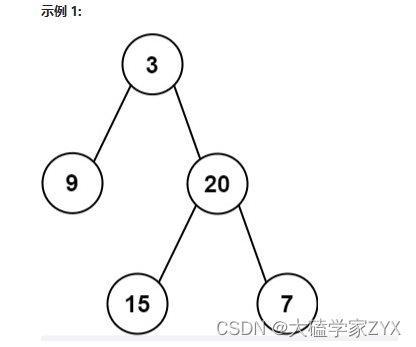
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
示例2
输入：inorder = [-1], postorder = [-1]
输出：[-1]

思路

本题的要求是从两个中序和后序遍历两个数组中构造一棵二叉树。

中序是左中右，后序是左右中，我们构造二叉树的时候首先要确定根节点的值，但中序是左中右，也不知道中节点在哪里，此时就需要结合后序。后序是左右中，也就是说，后序数组最后一个元素一定是根节点。

例如示例1，根节点一定是3，因为是后序（左右中遍历）数组的最后一个。

但是仅看后序无法区分左右，需要结合中序。当根节点是3的时候，左子树就是9，右子树就是15 20 7。能够直接确定左右子树里面所有的节点值。

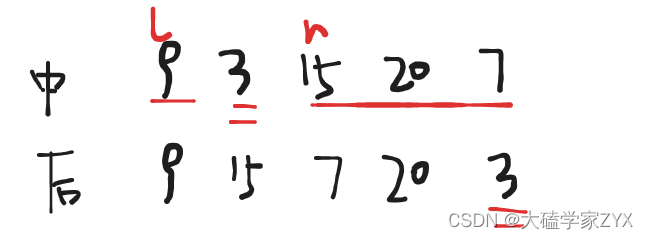
也就是说，我们先根据后序找到中间的节点，再根据中序和中间节点，在中序数组中完成左右子树切割的任务。

得到根节点左右子树后，再看后序数组，来明确左右子树的中间节点。根据后序左右中的顺序，可以知道右子树的中间节点是20。得到中间节点之后，再去切割中序，得到右子树中间节点的左右孩子是15和7。

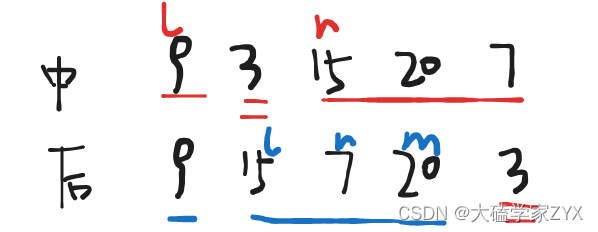
大致思路可以概括为

• 通过后序找到中间节点
• 通过中序区分左右子树的大区间
• 再根据大区间切割后序，在下一层递归的时候，再寻找左右子树大区间的中间节点。也就是找上一层节点的左右孩子。

伪代码

文字版代码思路：

• 后序数组为0，空节点
• 后序数组不为0，找到后序数组最后一个元素为根节点
• 寻找中序数组中根节点位置，切割得到根节点左右子树
• 寻找后序中左右子树区间的位置，找到区间最后一个元素就是左右子树的中间节点

//确定递归参数和返回值，返回二叉树的根节点
TreeNode* travelsal(vector<int>inorder,vector<int>postorder){if(postorder.size()==0){return null;}//找到分割点int val = postorder[postorder.size()-1];TreeNode* root = new TreeNode(val);//后序数组=1就直接返回rootif(postorder.size()==1){return root;}//单层递归逻辑int index;//寻找中序数组中根节点位置for(index=0;index<inorder.size();index++){if(inorder[index]==val){break;}}//break出来之后，此时的index就是根节点元素在中序数组的下标//切割中序数组，得到左中序数组和右中序数组//切割后序数组，切出左区间和右区间，并得到区间最后一个值就是左右孩子节点值//注意，切中序的时候已经知道了二叉树左区间，我们需要拿着中序数组左区间的大小去切后序数组//切割后序得到左后序数组和右后序数组,直接进行递归！root->left = travelsal(左中序数组，左后序数组);root->right = travelsal(右中序数组，右后序数组);return root;//返回二叉树}

后序数组如何切割出左右区间

后序数组确定了根节点之后，可以根据中序数组中得到的，左右区间的长度，在后序数组中切割出左区间和右区间。切割中序用的是index，切割后序用的是中序数组左右区间长度信息。

写法注意

因为切割过程比较复杂，我们可以先写递归的逻辑，看递归需要什么，再去前面部 分补充切割操作。

区间切割注意

切中序数组和切后序数组的时候，一定要统一区间的规则，统一为左闭右开或者左开右闭。区间切割规则如果不统一很容易出现边界值问题。

切的时候需要先切割中序，根据后序得到的根节点信息先把中序切开，再拿着中序得到的左区间，去切出来后序里面的左区间。

切区间的时候容易出问题，一定要打日志，要把中序数组和后序数组都打印出来，左中序/左后序也要打印出来。

中序和前序如何唯一构造二叉树

如果题目改成中序和前序，也能唯一构造出二叉树。中序是左中右，前序是中左右，我们可以根据前序数组先得到根节点（前序数组第一个），拿着中节点再去切中序数组。是同样的思路逻辑

后序和前序能否唯一构造二叉树？

不能。后序是左右中，前序是中左右，无法来区分左右区间，找不到分割点，就没办法进行切割。

中序把左右区间隔开的逻辑，才能知道左区间是什么，右区间是什么。

例如图上这种情况，就不能对此做出区分，但是这两棵二叉树是完全不同的二叉树。

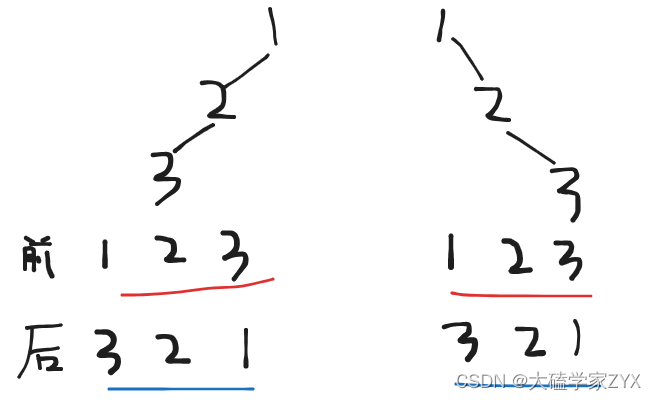
补充：

在上图结构的二叉树中

    1/2/
3

前序遍历的顺序是“根左右”，后序遍历的顺序是“左右根”。

• 前序遍历：

  遵循“根左右”的顺序，先访问根节点1，然后访问左孩子2，再访问2的左孩子3，所以前序遍历的结果是 1-2-3。

• 后序遍历：

  遵循“左右根”的顺序。由于这棵树没有右孩子，所以我们首先访问左孩子，即访问2，由于中间节点需要在最后访问，因此我们先不把2计入结果，继续访问2的左孩子3。在最后的结果中，对于每一棵子树，都是先写叶子节点，再写根节点，所以后序遍历的结果是 3-2-1。

后序访问方式的一个好处是，对于每一个节点，我们在访问该节点之前，已经访问了其所有子节点。这在一些算法问题中是非常有用的，比如计算树的高度，或者判断一棵树是否是另一棵树的子树等。

完整版

• 第一步先把除了切割左中序/左后序数组的逻辑写完，主要是递归的逻辑
• 本题是遍历，两个数组大小相同且是否为空也相同

class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//返回二叉树的根节点//如果数组大小是0，空节点if(inorder.size()==0&&postorder.size()==0){return NULL;}//找到根节点的元素值int val = postorder[postorder.size()-1];//给根节点赋值TreeNode* root = new TreeNode(val);//找中序数组中的根节点int index = 0;for(index;index<inorder.size();index++){if(inorder[index]==val){break; //跳出循环，相当于存储中序数组中val值的下标}}//根据得到的下标值，切割左中序数组//根据左中序数组的长度，切割左后序数组root->left = buidTree(左中序，左后序);root->right = buildTree(右中序，右后序);return root;}
};

• 写好框架之后再来填写切割数组的逻辑
• 切割的时候注意保持一致的切割原则！坚持循环不变量，这个原则在之前的螺旋数组里也很重要

切割中序数组

       //找中序数组中的根节点int index = 0;for(index;index<inorder.size();index++){if(inorder[index]==val){break; //跳出循环，相当于存储中序数组中val值的下标}}//根据得到的下标值，切割左中序数组，建立新的数组//左闭右开区间[0,index)vector<int>leftInorder(inorder.begin(),inorder.begin()+index);vector<int>rightInorder(inorder.begin()+index+1,inorder.end());

vector数组创建

构造函数:

// 1. 创建空vector; 常数复杂度
vector<int> v0;
// 1+. 这句代码可以使得向vector中插入前3个元素时，保证常数时间复杂度
v0.reserve(3);
// 2. 创建一个初始空间为3的vector，其元素的默认值是0; 线性复杂度
vector<int> v1(3);
// 3. 创建一个初始空间为3的vector，其元素的默认值是2; 线性复杂度
vector<int> v2(3, 2);
// 4. 创建一个初始空间为3的vector，其元素的默认值是1，
// 并且使用v2的空间配置器; 线性复杂度
vector<int> v3(3, 1, v2.get_allocator());
// 5. 创建一个v2的拷贝vector v4， 其内容元素和v2一样; 线性复杂度
vector<int> v4(v2);
// 6. 创建一个v4的拷贝vector v5，其内容是{v4[1], v4[2]}; 线性复杂度
vector<int> v5(v4.begin() + 1, v4.begin() + 3);
// 7. 移动v2到新创建的vector v6，不发生拷贝; 常数复杂度; 需要 C++11
vector<int> v6(std::move(v2));  // 或者 v6 = std::move(v2);

上面左中序数组的创建，使用的就是创建拷贝vector的方式

vector<int>leftInorder(inorder.begin(),inorder.begin()+index);

cppSTL定义区间默认的左闭右开规则

在C++中，当使用迭代器定义一个区间时，通常采用的是左闭右开的方式，即包含区间的起始位置，但不包含区间的结束位置。这一规则在大部分STL容器，包括vector，list，deque等的成员函数中都是通用的。

例如：

vector<int> v5(v4.begin() + 1, v4.begin() + 3);

新创建的v5包含的元素是v4[1]和v4[2]（v4的下标从0开始，因此v4.begin() + 1指向的就是v4[1]），但是，并不包含v4.begin() + 3所指向的元素。也就是说，并不包含v4[3]。

由于迭代器定义区间默认是左闭右开原则，因此，本题中切割数组最好也是左闭右开。例如，下面的代码构造新的左中序数组：

vector<int>leftInorder(inorder.begin(),inorder.begin()+index);

默认定义的就是左闭右开的区间，这句代码构造了一个inorder数组的拷贝数组，包含的元素从inorder[0]一直到inorder[index-1]。并不包含inorder[index]。

关于左闭右开原则cpp适用性

在C++的**STL**（Standard Template Library，标准模板库）中，区间通常被定义为左闭右开，也就是说，区间包含开始位置但不包含结束位置。这个约定对于所有STL容器的成员函数都是适用的，例如vector、list、deque等的begin()、end()、rbegin()、rend()等函数。

对于非STL的一般编程情况，是否使用左闭右开的规则取决于程序员自己。左闭右开的优势在于它能够简化编程，因为在这种情况下，一个区间的结束位置正好是下一个区间的开始位置。

切割后序数组

		//根据切割得到的左中序和右中序数组的长度，对后序数组进行切割//左中序长度=左后序，右中序长度=右后序//后序数组先删除末尾元素，因为是根节点postorder.pop_back();//切割出左后序vector<int>leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());//切割出右后序vector<int>rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());

补全的完整版

class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//返回二叉树的根节点//如果数组大小是0，空节点if(inorder.size()==0&&postorder.size()==0){return NULL;}//找到根节点的元素值int val = postorder[postorder.size()-1];//给根节点赋值TreeNode* root = new TreeNode(val);//找中序数组中的根节点，也就是分割点int index;for(index=0;index<inorder.size();index++){if(inorder[index]==val){break; //跳出循环，相当于存储中序数组中val值的下标}}//根据得到的下标值，切割左右中序数组//左闭右开区间[0,index)vector<int>leftInorder(inorder.begin(),inorder.begin()+index);vector<int>rightInorder(inorder.begin()+index+1,inorder.end());//根据左中序数组的长度，切割左右后序数组//后序数组先删除末尾元素，因为是根节点postorder.pop_back();//切割出左后序vector<int>leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());//切割出右后序vector<int>rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());//递归root->left = buildTree(leftInorder,leftPostorder);root->right = buildTree(rightInorder,rightPostorder);return root;}
};