1. 算法简介
递推和递归虽然叫法不同,但它们的基本思想是一致的,在很多程序中,这两种算法可以通用,不同的是递推法效率更高,递归法更方便阅读。
(1)递推法
递推法是一种重要的数学方法,同时也是计算机进行数值计算的个重要算法。
递推法的核心是找到计算前后过程之间的数量关系,即递推式。递推式往往根据已知条件和所求问题之间存在的某种相互联系推导得出。递推计算时,需要将复杂运算转换为若干步重复的简单运算,这样可以发挥计算机擅于重复处理数据的特点。递推法避开了求通项公式的麻烦,把一个复杂问题的求解分解成了连续的若干歩简单运算,可以将递推法看成一种特殊的迭代算法。
[案例解析]铺方格
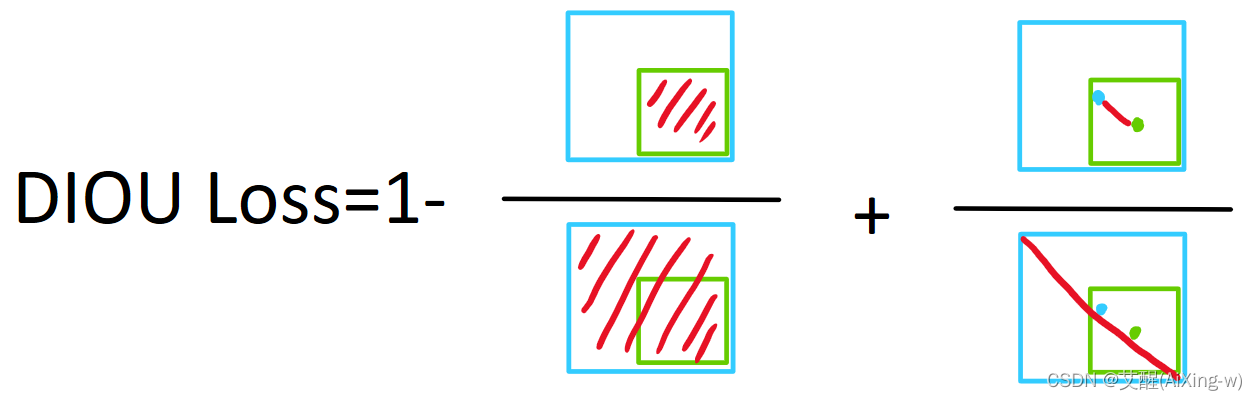
有2×n个长方形的方格,用一个1×2的骨牌铺满方格。例如当0=3时为2×3方格,骨牌的铺放方案有3种,

骨牌铺设方案(1)
编写一个程序,试对给出的任意一个n(n>0)输出铺法总数。针对这个问题,要想直接获得问题的解答是相当困难的。可以用递推法,从简单到复杂逐步归纳出问题解的一般规律。分析过程如下。
当n=1时,只能有一种铺法 ,如图4-2(a)所示,铺法总数为X1=1。
当n=2时,骨牌可以并列竖排,也可以并列横排,再无其他排列方法,如图2(b)所示,铺法总数为X2 =2。
当n=3时,骨牌可以全部竖排,也可以认为在方格中已经有一个竖排骨牌、需要在方格中排列两个横排骨牌(无重复方法),若已经在方格中排列两个横排骨牌,则必须在方格中排列一个竖排骨牌,如图2(c)所示,再无其他排列方法,铺法总数为X3= 3。

骨牌铺放方案(2)
由此可以看出,当n=3时,排列骨牌的方法数是n=1和n=2时排列方法数之和。
推出一般规律,对一般的n,要求Xn。可以这样考虑:若第一个骨牌是竖排列,则剩下n-1个骨牌需要排列,这时排列方法数为Xn-1,若第一个骨牌是横排列,则整个方格至少有2个骨牌是横排列(1×2骨牌),因此剩下n-2个骨牌需要排列,这时排列方法数为Xn-2从第一种骨牌排列方法考虑,只有这两种可能,所以有:
Xn=Xn-1+Xn-2(n> 2)
X1=1
X2=2
Xn=Xn-1+ Xn-2就是问题求解的递推公式
任意n都可以从中获得解答。
例如n=5,
X3=X2+X1=3
X4=X3+X2=5
X5=X4+X3=8
利用程序表示为:
cin>>n;
a[1]=1;a[2]=2;
for(i=3;i<=n; i++)
a[i]=a[i-1]+a[i-2];
cout<<a[n]<<"";(2)递归法
在计算机科学中,如果某个函数的实现中出现了对函数自身的调用语句,则称该函数为递归函数。
递推法可以用递归函数实现。一般来说,循环递推法比递归函数的速度更快,但递归函数的可读性更强。
例如,上述平铺方格问题改写成递归函数的形式如下。
int pu(int n)
{
if(n==1) return 1;
if(n==2) return 2;
return pu(n-1) +pu(n-2);
}递归函数在它的函数体内直接或者间接地调用自身,每调用一次,就进入新的一层。递归函数必须有结束递归的条件。函数会一直递推 ,直到遇到结束 条件返回,递归函数调用的一般过程如图3所示,这里以n=6为例。
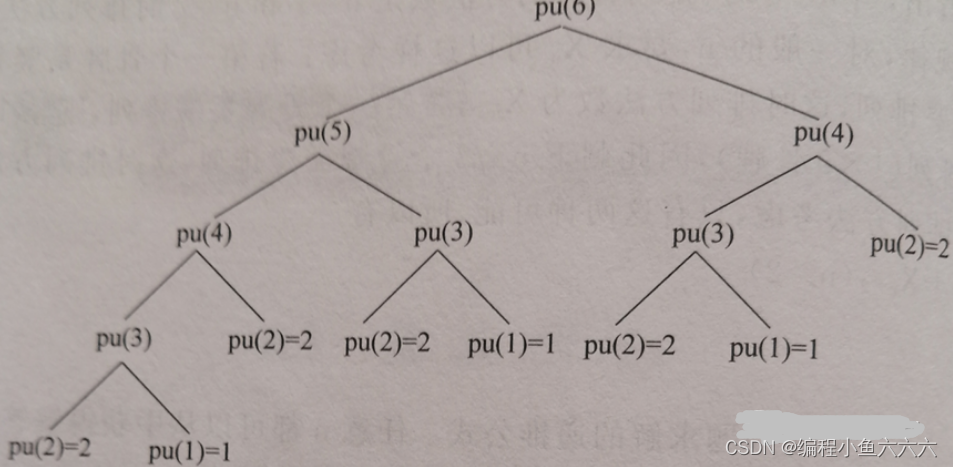
递归函数的调用过程
2. 取数位(2017年试题E)
【问题描述】
求一个整数的第k位数字有很多种方法,以下下方法就是其中一种。
//求x用十进制表示时的数位长度
int len(int x){
if(x<10) return 1;
return len(x/10)+1;
}
//取x的第k位数字
int f(int x, int k) {
if(len(x)-k==0) returnx%10;
return ( ) ;//填空
}
int main()
int x= 23574;
printf("&d\n", f(x,3));
return 0;
}对于题目中的测试数据,应该打印5。
请仔细分析源码,并补充画线部分缺少的代码。
注意:只提交缺失的代码,不要填写任何已有内容或说明性文字。
答案——取数位
//求 x 用十进制表示时的数位长度int len(int x){if(x<10) return 1;return len(x/10)+1;}//取 x 的第 k 位数字int f(int x, int k) {if(len(x)-k==0) return x%10;return f(x/10,k) ;//填空}int main()int x= 23574;printf("&d\n", f(x,3));return 0;}