BP神经网络
- 神经网络介绍
- 前馈神经网络
- BP神经网络
- BP神经网络的核心思想
- 误差反向传播算法
- BP网络结构
- 反馈神经网络
- 自组织神经网络
- 神经网络相关概念
- 激活函数
- Sigmoid函数
- tanh双曲正切函数
- ReLU函数
- Leaky RuLU函数
- Maxout函数
- 激活函数的选择
- 损失函数
- Softmax
- 交叉熵
- 均方差损失函数
- 自定义函数
- 学习率
- 过拟合
- 模型训练中的问题
- 神经网络效果评价
神经网络介绍
神经网络的训练目的是希望能够学习到一个模型,实现输出一个期望的目标值。
学习的方式是在外界输入样本的刺激下不断改变网络的连接权值。
传统神经网络主要分为以下几类:前馈型神经网络,反馈型神经网络和自组织神经网络。
- 前馈神经网络将神经元分层排列,分别是输入层、中间层和输出层。按照层数不同,划分为单层前馈神经网络和多层前馈神经网络。如感知机、BP网络、RBF网络。
- 反馈神经网络每个神经元同时将自身的输出信号作为输入信号反馈给其他神经元,Hopfield神经网络是反馈网络中最简单且应用广泛的模型。
- 自组织神经网络是无导师学习网络通常采用竞争原则进行网络学习。
前馈神经网络
前馈神经网络(Feed Forward Neural Network) 是一种单向多层的网络结构,即信息是从输入层开始,逐层向一个方向传递,一直到输出层结束。
所谓的**“前馈”是指输入信号的传播方向为前向**,在此过程中并不调整各层的权值参数,而反传播是将误差逐层向后传递,从而实现使用权值参数对特征的记忆,即通过反向传播(BP) 算法来计算各层网络中神经元之间边的权重。
BP算法具有非线性映射能力,理论上可逼近任意连续函数,从而实现对模型的学习。
BP神经网络
BP神经网络训练过程的基本步骤可以归纳如下:
- 初始化网络权值和神经元的阈值,一般通过随机的方式进行初始化
- 前向传播:计算隐层神经元和输出层神经元的输出
- 后向传播:根据目标函数公式修正权值 w i j w_{ij} wij
上述过程反复迭代,通过损失函数和成本函数对前向传播结果进行判定,并通过后向传播过程对权重参数进行修正,起到监督学习的作用,一直到满足终止条件为止。
BP神经网络的核心思想
由后层误差推导前层误差,一层一层的反传,最终获得各层的误差估计,从而得到参数的权重值。
由于权值参数的运算量过大,一般采用梯度下降法来实现。
所谓梯度下降就是让参数向着梯度的反方向前进一段距离,不断重复,直到梯度接近零时停止。此时,所有的参数恰好达到使损失函数取得最低值的状态,为了避免局部最优,可以采用随机化梯度下降。
误差反向传播算法
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用最广泛的神经网络。
BP神经网络的基本思想是梯度下降法,利用梯度搜索技术,以期使网络的实际输出值和期望输出值的误差均方差为最小。
算法包括信号的前向传播和误差的反向传播,即计算误差输出时,按从输入到输出的方向进行;而调整权值和阈值时,按从输出到输入的方向进行:
- 正向传播时,输入信号通过隐含层作用于输出结点,经过非线性变换,产生输出信号,若实际输出与期望输出不相符,则转入误差的反向传播过程。
- 误差的反向传播是将输出误差通过隐含层向输入层逐层反传,并将误差分摊给各层所有单元,以从各层获得的误差信号作为调整各单元权值的依据,所以称该算法为误差反向传播算法。
BP网络结构
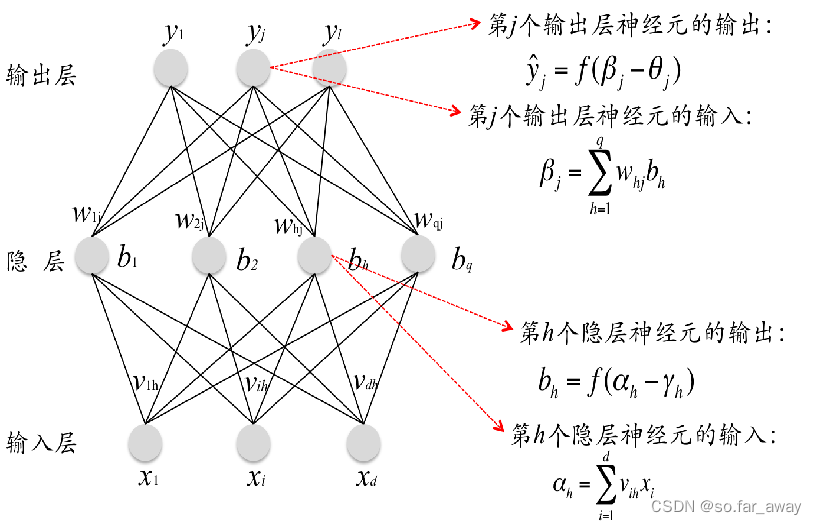
其中, f ( x ) = s i g m o i d ( x ) = 1 1 + e − x f(x)=sigmoid(x)=\frac{1}{1+e^{-x}} f(x)=sigmoid(x)=1+e−x1
网络模型的训练目标为找出合适的权值和阈值使得误差E最小:
E = 1 2 ∑ j = 1 l ( y j ^ − y j ) 2 E=\frac{1}{2}\sum_{j=1}^{l}(\hat{y_j}-y_j)^2 E=21∑j=1l(yj^−yj)2
反馈神经网络
- 与前馈神经网络相比,反馈神经网络内部神经元之间有反馈(即非单向),可以用一个无向完全图表示,包括了Hopfield 网络、BAM网络,Elman网络等。
- Hopfield网络类似人类大脑的记忆原理,即通过关联的方式,将某一件事物与周围场中的其他事物建立关联,当人们忘记了一部分信息后,可以通过场中信息回忆起来,将缺失的信息找回。通过在反馈神经网络中引入能量函数的概念,使其运行稳定性的判断有了可靠依据,由权重值派生出能量函数是从能量高的位置向能量低的位置转化,稳定点的势能比较低。基于动力学系统理论处理状态的变换,系统的稳定态可用于描述记忆。
- Hopfield网络分为离散型和连续型两种网络。
- 在Hopfield网络中,学习算法是基于Hebb学习规则,权值调整规则为若相邻两个神经元同时处于兴奋状态,那么他们之间的连接应增强,权值增大;反之,则权值减少。
自组织神经网络
自组织神经网络又称Kohonen网,这一神经网络的特点是当接收到外界信号刺激时,不同区域对信号自动产生不同的响应。
这种神经网络是在生物神经元上首先发现的,如果神经元是同步活跃的则信号加强,如果异步活跃则信号减弱。
神经网络相关概念
激活函数
激活函数经常使用Sigmoid函数、tanh函数、ReLu 函数
激活函数通常有以下性质:
- 非线性
- 可微性
- 单调性
- f(x)≈x
- 输出值范围
- 计算简单
- 归一化
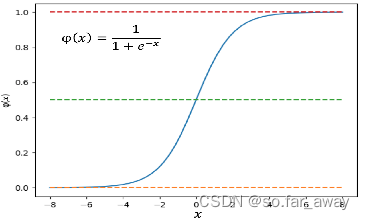
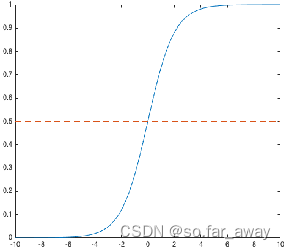
Sigmoid函数
优点:
- 输出范围有限,数据在传递的过程中不容易发散,并且其输出范围为(0,1),可以在输出层表示概率值。
- Sigmoid函数的导数是非零的,很容易计算。
缺点:
- 梯度下降非常明显,且两头过于平坦,容易出现梯度消失的情况,输出的值域不对称,并非像tanh函数那样值域是-1到1。
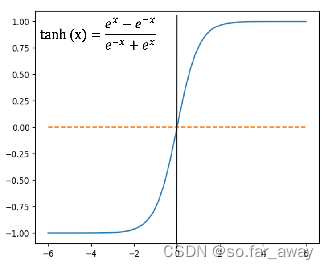
tanh双曲正切函数
- 双曲正切函数将数据映射到[-1,1],解决了Sigmoid函数输出值域不对称问题。
- 它是完全可微分和反对称的,对称中心在原点。
- 它的输出值域两头依旧过于平坦,梯度消失问题仍然存在。
- 为了解决学习缓慢和梯度消失问题,可使用其更加平缓的变体,如log-log、Softsign、Symmetrical Sigmoid等。
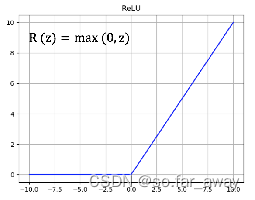
ReLU函数
- ReLU函数是目前神经网络里常用的激活函数。
- 由于ReLU函数是线性特点使其收敛速度比Sigmoid、Tanh更快,而且没有梯度饱和的情况出现。计算更加高效,相比于Sigmoid、Tanh函数,只需要一个阈值就可以得到激活值,不需要对输入归一化来防止达到饱和。
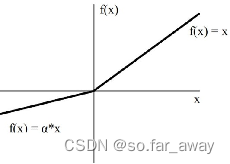
Leaky RuLU函数
带泄漏修正线性神经元( Leaky RuLU)的出现是解决“死亡神经元”的问题。
f ( x ) = { a x , x < 0 x , x ≥ 0 f(x)=\begin{cases} ax, & \text x<0 \\ x, & \text x≥0 \end{cases} f(x)={ax,x,x<0x≥0
Maxout函数
Maxout是一种分段线性函数,理论上可以拟合任意凸函数,与其它激活函数相比,它计算k次权值,从中选择最大值作权值,所以其计算量成k倍增加。
当k为2时,可看成是分成两段的线性函数,它的函数公式如下:
m a x ( w 1 T x + b 1 , w 2 T x + b 2 ) max(w_1^Tx+b_1,w_2^Tx+b_2) max(w1Tx+b1,w2Tx+b2)
激活函数的选择
- 通常使用ReLU函数,并注意设置好学习率
- 如果存在死亡神经元的问题,就尝试Leaky ReLU或Maxout函数
- 尽量避免使用Sigmoid函数
- tanh函数大部分情况下效果不如ReLU和Maxout函数
损失函数
- 损失函数评价的是模型对样本拟合度,预测结果与实际值越接近,说明模型的拟合能力越强,对应损失函数的结果就越小;反之,损失函数的结果越大。
- 损失函数比较大时,对应的梯度下降比较快。
- 为了计算方便,可以采用欧式距离作损失度量标准,通过最小化实际值与估计值之间的均方误差作为损失函数,即最小平方误差准则(MSE):
m i n C ( Y , G ( X ) ) = ∣ ∣ G ( X ) − Y ∣ ∣ 2 = ∑ i ( G ( x i ) − y i ) 2 minC(Y,G(X))=||G(X)−Y||^2=∑_i(G(x_i)−y^i)^2 minC(Y,G(X))=∣∣G(X)−Y∣∣2=i∑(G(xi)−yi)2 - 其中G(X)是模型根据输入矩阵X输出一个预测向量,预测值G(X)和真值Y的欧式距离越大、损失就越大,反之就越小,即求 ∣ ∣ G ( X ) − Y ∣ ∣ 2 ||G(X)−Y||^2 ∣∣G(X)−Y∣∣2的极小值。
- 如果是批量数据,则将所有数据对应模型结果与其真实值之间的差的平方进行求和。
- 合适的损失函数能够确保深度学习模型更好地收敛,常见的损失函数有Softmax、欧式损失、Sigmoid交叉熵损失、Triplet Loss、Moon Loss、Contrastive Loss等。
Softmax
- 使用Softmax函数的好处是可以使分类问题的预测结果更加明显,不同类别之间的差距更大。
- 在实际应用中,特别是在Tensorflow中推荐采用交叉熵与Softmax结合作为损失函数,可以避免数值不稳定的情况。
交叉熵
- 目标为 二分类问题,分类误差越小,则损失越小,对正负分类计算各自的损失。
- 会产生梯度爆炸问题:
L ( w ) = 1 N ∑ n = 1 N H ( p n , q n ) = − 1 N ∑ n = 1 N [ y n l o g y n ^ + ( 1 − y n ) l o g ( 1 − y n ^ ) ] L(w)=\frac{1}{N}∑_{n=1}^NH(p_n,q_n)=−\frac{1}{N}∑_{n=1}^N[y_nlog\hat {y_n}+(1−y_n)log (1−\hat {y_n})] L(w)=N1n=1∑NH(pn,qn)=−N1n=1∑N[ynlogyn^+(1−yn)log(1−yn^)] - 交叉熵损失函数的用途主要应用在互相排斥的分类任务中。
- 交叉熵也可以用于目标为[0,1]区间的回归问题。
均方差损失函数
M S E = 1 n ∑ i = 1 n ( y i − t i ) 2 MSE=\frac{1}{n}∑_{i=1}^n(y_i−t_i)^2 MSE=n1i=1∑n(yi−ti)2
自定义函数
对于某些候选属性,单独将一些预测值取出或者赋予不同大小的参数。或者合并多个损失函数,实现多目标训练任务,或者在不同的情况下采用不同的损失函数。
学习率
学习率控制每次更新参数的幅度,过高和过低的学习率都可能对模型结果带来不良影响,合适的学习率可以加快模型的训练速度。
常见学习率调整方法:
- 基于经验的手动调整
- 固定学习率
- 均分分步降低策略
- 指数级衰减
- 多项式策略
- AdaGrad动态调整
- AdaDelta自动调整
- 动量法动态调整
- RMSProp动态调整
- 随机梯度下降
- Adam自动调整
过拟合
过拟合是指模型在训练集上预测效果好,但在测试集上预测效果差。
常用的防止过拟合的方法有:
- 参数范数惩罚
- 数据增强
- 提前终止
- Bagging等集成方法
- Dropout
- 批正则化
模型训练中的问题
- 选择恰当的激活函数
- 权重初始化
- 学习率
- 使用Dropout正则化
- 周期 / 训练迭代次数
- 训练过程可视化
神经网络效果评价
- 用于分类的模型评价以**准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1分值(F1 Score)**为主,辅以ROC、AUC并结合实际应用进行结果评价。
- 如果神经网络用于聚类,数据源并没有进行标记,那么其模型结果的评价按照聚类算法的标准来操作,如RMSSTD、R Square、SRP等。
- 随着机器学习在不同领域中的应用,其评价方式需要与实际业务相结合,通过确定目标要求来定量设计评价标准,例如在目标检测等方面使用平均曲线下面积(mean Average Precision, mAP)指标进行衡量识别准确性。