噪 声

一. 噪声定义

  从物理学的角度来看：噪声是发声体做无规则振动时发出的声音。在图形学中，我们把各种妨碍人们对其信息接受的因素称为图像噪声 。噪声在理论上可以定义为“不可预测，只能用概率统计方法来认识的随机误差”。因此将图像噪声看成是多维随机过程是合适的，因而描述噪声的方法完全可以借用随机过程的描述，即用其概率分布函数和概率密度分布函数。由此看来，噪声是百无一用了，确实，因为噪声的出现，让图像变得不够完美和有缺陷，所以好多时候我们都在想尽办法去除噪声。但事情总是两面的，如一刀，你可以用来切菜砍柴，也可以杀人越货，但对刀本身来说，它是中性的，不存在好与不好的概念。噪声也一样，它可能会把图像搞得很糟，但也可能会制造出令人瞠目结舌的效果。

  噪声种类很多，在不同的领域，噪声有不同的定义和应用，我们的讨论仅仅局限于图像处理方面，图像处理其实也是个很大的类别，加之前人的研究涉猎范围非常广，我们的讨论也只局限于图像处理中应用非常广的几种噪声，从我查阅的资料来看，没有找到成体系的介绍图像和游戏图形处理方面的噪声资料。但实事上，噪声在图像处理和游戏中应用如此之广，以至于我们或多或少都与噪声打过交道。接下来的几篇文章，我们会从最简单的入手，系统的讨论一下噪声类型、原理及应用。

  笔者认为，噪声其实就是随机数，根据随机数出现的频率、分布函数的不同而有区别。随机数如果太随机了，分布毫无规律则没什么用，因为就只是噪点了，所以实际有用的是那些看似随机，但实际受某种规律约束的噪声。就像自然界里的蜂巢结构、长颈鹿身上的花纹、植物叶片的纹理，看似没有规律，实际上却是受到某种神秘力量的控制，爱因斯坦、牛顿、沃罗诺伊、图灵等科学家都进行过研究，也建立起了数学模型。

  上面的两张图看似随机，但其实规律又很明显，自然界之神奇，从细胞结构到宇宙的变幻无不受某种神秘力量的约束。很多科学家也为之惊叹，并作出了不懈努力去破解个中缘由。

  这两张图片是用有规律随机数（噪声）生成的模拟图，神奇如斯，这就是噪声和数学的魅力，合理的利用噪声可以产生让人匪夷所思的神奇效果，而这种效果有时往往用定量的方法没办法生成。

二. 图形学中的常见噪声

  图形图像中，常用的噪声也很多，按照分类的不同，可以有不同的分法，比如按照噪声分布函数分，可以分为高斯噪声、瑞利噪声、伽马(爱尔兰)噪声、指数分布噪声、均匀分布噪声、脉冲噪声、椒盐噪声等等，按照噪声生成方式可以分为单噪声和合成噪声（分形噪声），单噪声指的是使用一种方式生成的一种频率，振幅的噪声，分形噪声是对多种频率，振幅噪声的合成。按照产生噪声所使用方法的不同可以分为梯度噪声和值噪声，值噪声仅使用点值来产生噪声，如Worley噪声和Voronoi噪声，而梯度噪声生成时不仅用到点值，还需要用到一个梯度值，通过点值与梯度值的运算来产生噪声，如Perlin噪声和Simplex噪声。因为梯度噪声和值噪声产生的噪声再进行分形叠加，可以很好的模拟自然现象，我们也主要就只关注这几种噪声的生成和运用。

(一)白噪声

  白噪声（white noise）是指功率谱密度在整个频域内均匀分布的噪声。 所有频率具有相同能量密度的随机噪声称为白噪声。也就是说，白噪声是完全随机的，它不偏袒任何频率，所以看起来很均匀。因此，白噪声只具有统计学上的意义，单独讨论一个噪声点几乎没用意义。

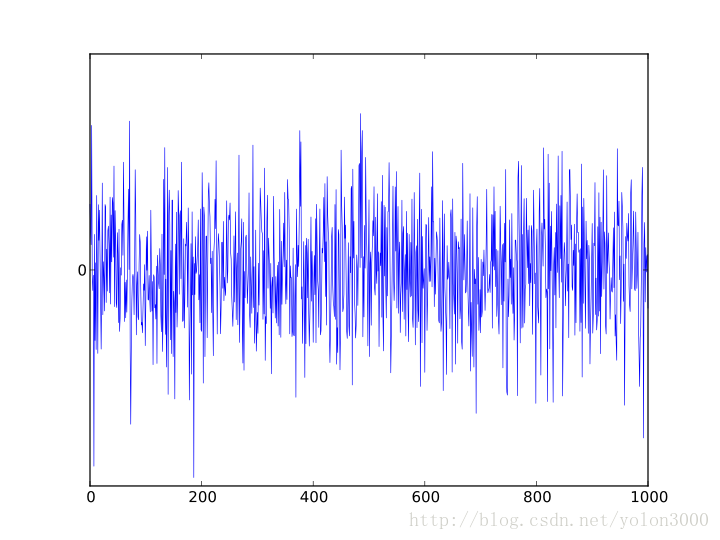
  这就是白噪声的波型，直观的印象，这跟我们平时见到的音频波型最大的区别就是白噪声波型几乎没有什么高低起伏、轻重缓急。

  这是白噪声的二维纹理，分布相对很均匀。白噪声通常是作为一种背景噪声出现，很多时候都是非我们意愿的。

(二)Perlin噪声（Gradient噪声）

  Perlin噪声是由Ken Perlin于1983年提出来的一种基于梯度（Gradient）的噪声，Perlin噪声一经提出即被广泛应用，主要是Perlin噪声生成噪声看似离散实则有非常好的聚合性，能用来模拟山脉，果冻体和流体，下面是Perlin噪声生成的二维噪声图。

  初一看，Perlin噪声很像积雨云，原始的Perlin噪声看起来很模糊，不锐利，没有细节，但通过分形叠加，可以产生各种频率、各种幅度、各种波长的细节，可以模拟从大尺度到小尺度的自然现象。

(三)Simplex噪声（Gradient噪声）

  Simplex噪声是由Ken Perlin于2001年对Perlin噪声的改进，主要是优化了缓释函数和改进了高维度性能，因此Simplex在高维和高阶时有更好的连续性和性能表现。

  看起来，Simplex噪声跟Perlin噪声没什么不同，但理解来说相对要复杂一些。

(四)Worley噪声（Value噪声）

  Worley噪声是一种典型的值噪声，Worley噪声特别适合用来模拟像蜂巢，长颈鹿花纹，也是一种孔状程序纹理生成方法。

  从上图可以看到，Worley噪声生成的纹理与Perlin噪声生成的纹理还是有比较大的区别的。

(五)Voronoi噪声（Value噪声）

  Voronoi噪声其实叫Voronoi 图（ Voronoi diagram），在数学上，Voronoi图用来依据离散点将一个平面切分成一系列的子平面，生成的子平面又中Voronoi图元（Voronoi cells），Voronoi噪声生成的纹理与Worley噪声生成的纹理又一些相似之处。

  Voronoi噪声用来模拟叶片纹理或者细胞结构有时效果会非常好。

三. 图形学中的距离算法类型

(一)Euclidean Distance

  欧几里得距离（euclidean Distance）（也称欧氏距离）是一个通常采用的距离定义，也是最好理解的距离，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。这个距离就是我们平时在数学里的距离，计算公式很简单：
在二维空间中，设a(x,y),b(x,y)为二维空间中的两点，则欧几里得距离的计算公式如下：

$$distance = \sqrt{(a.x-b.x)^2+(a.y-b.y)^2}$$
公式很容易推广到三维空间中，设a(x,y,z),b(x,y,z)为三维空间中的两点，则欧几里得距离的计算公式如下：
$$distance = \sqrt{(a.x-b.x)^2+(a.y-b.y)^2+(a.z-b.z)^2}$$
同样，公式可以很容易的推广到三维以上的n维空间。
  可以看到，欧几里得距离即是两点之间真实的直线距离，这个距离在我们日常生活中也是用得最多的，但是，从计算来看，这个距离的计算有乘方、还有开方，计算时性能需要留心，特别是在大规模底层运算时，这个性能开销还是很大的。

(二)Manhattan Distance

  曼哈顿距离（Manhattan Distance）用以标明两个点在标准坐标系上的绝对轴距总和，曼哈顿距离可以理解为在纵横棋盘上行子，在只能上下左右移动，不能斜线移动时棋子从一个地方移动到另一个地方的距离。在早期的计算机图形学中，计算机硬件有限，浮点运算代价昂贵，科学家们为了用整数方法处理屏幕像素而发明这种方法，方法简单，运算快捷，而且因为是整数，不会导致误差累积。
  设a(x,y),b(x,y)为二维空间中的两点，则在二维空间中曼哈顿距离计算公式如下：

$$distance=|a.x-b.x|+|a.y-b.y|$$
  同样，可以很方便的推广到三维，设a(x,y,z),b(x,y,z)为三维空间中的两点，则在三维空间中曼哈顿距离计算公式如下：
$$distance=|a.x-b.x|+|a.y-b.y|+|a.z-b.z|$$
  当然，也可以很轻松的推广到n维空间，从曼哈顿距离的计算公式可以看出，曼哈顿距离计算简单方便，计算代价小。

(三)Chebyshev Distance

  切比雪夫距离（Chebyshev Distance）定义的是两点之间其各坐标数值差绝对值的最大值。若将国际象棋棋盘放在二维直角坐标系中，格子的边长定义为1，座标的x轴及y轴和棋盘方格平行，原点恰落在某一格的中心点，则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离，因此切比雪夫距离也称为棋盘距离。任何一个不在棋盘边缘的位置，和周围八个位置的切比雪夫距离都是1。

  由切比雪夫距离的定义可以得到它的计算公式，设a(x,y),b(x,y)为二维空间中的两点，则在二维空间中切比雪夫距离计算公式如下：
$$distance=max(|a.x-b.x|,|a.y-b.y|)$$
  推广到三维，设a(x,y,z),b(x,y,z)为三维空间中的两点
$$distance=max(|a.x-b.x|,|a.y-b.y|,|a.z-b.z|)$$
  根据定义，也可以很方便的把切比雪夫距离推广到n维空间，除此之外，常用的距离还有闵可夫斯基距离(Minkowski Distance)、 标准化欧氏距离 (Standardized Euclidean distance )、马氏距离(Mahalanobis Distance)等，但我们一般就只用到前面介绍的这三种距离。其他的不再赘述。

  关于这三种距离，切比雪夫距离只是求个最大值，最好理解。关于欧几里得距离和曼哈顿距离可以看下面的这张图，这张图可以很明确的看到这两种距离的差异。

  图中红线代表曼哈顿距离，绿线代表欧几里得距离，而蓝色和黄色代表等价的曼哈顿距离。从这三种距离计算公式可以看到，欧几里得距离计算量是最大的，曼哈顿距离和切比雪夫距离则相对简单。我们在应用中，有时我们并不是为了得到距离而计算距离，有时只是为了比较两个“距离”大小，这时，对欧几里得距离来说，开方是不必要的，这时我们可以不开方，因为是用来作比较，开不开方不会影响结果。这时可以使用这种变形的欧几里得距离，可以大大减少计算量。

四. 几种随机数生成方式

  随机数发生器理解起来很简单，但要得到真正随机分布的随机数却并不那么容易，随机数大致可以分成两类，一类是非相关的，即本次产生的随机数与上次产生的随机数没有关系，随机数产生不具备可重复性（Reproduceable）,另一类是相关的，即本次产生的随机数与上次产生的随机数有关，给定一个相同的输入，产生一个相同的输出，随机数产生具备可重复性（Reproduceable）。

(一)HASH

  hash函数是我们平时用得最多的函数之一，可以用hash来生成地址，可以用hash来排序，可以用hash作加密生成摘要等，hash函数也可以当成随机数发生器使用，给它一个种子，就能到了一个随机值，hash函数的均匀性与我们构造的hash函数有关，通常，在我们对随机数产生要求不高或者把它作用另一个随机数发生器的种子时，选择Hash函数作一个中间件使用。在图形学中，我们希望取得的值在[－1，1]之间，比如下面这个hash函数，它的返回值域就是[－1，1],这也是我们经常会用到的随机数发生器之一。

float hash(int x)
{      x = (x<<13) ^ x;return ( 1.0 - ( (x * (x * x * 15731 + 789221) + 1376312589) & 7fffffff) / 1073741824.0);
}

float hash(vec2 p)
{return fract(sin(dot(p, vec2(12.9898, 78.233))) * 43758.5453);// 下面这个更好，但可能在mac机子上会有些问题。//return fract(sin(dot(p, vec2(1.0,113.0)))*43758.5453123);}vec3 hash( vec3 p )
{p = vec3( dot(p,vec3(127.1,311.7, 74.7)),dot(p,vec3(269.5,183.3,246.1)),dot(p,vec3(113.5,271.9,124.6)));return fract(sin(p)*43758.5453123);
}

(二)LCG

  LCG(Linear Congruential Generator)线性同余发生器。这个随机数发生器目前用得非常广，从它的名字可以看出，它的计算方式是对一个线性函数取余，它的每个随机数都与之前产生的随机数有关，其计算公式可以写为

N(i) = (a*N(i-1)+c) % m

  其中，m>0, 0 < a < m,0 <＝ c < m, 参数a,c,m的选择很重要，他们将直接影响随机数产生的质量。
  为了得到足够大的随机数范围，这里m需要取一个很大的值，不然重复性将大大增加，从而导致随机性不足。Lehmer于1951年已经证明，该随机数生成的数在（0，1]之间分布均匀，这也符合我们期望。该算法应用如此之广，Microsoft的随机数发生器Rand()就是采用了LCG，其中a=214013,c=2531011,m=2^32,N（1）=1。刚才提到了，该随机数发生器的值会均匀的分布在(0,1]范围内，所以Rand()产生随机数可能性小于等于m=2^32,这个数还是不够大，只能满足一般应用。当然可以通过添加种子那产生更随机的结果。
  当然，还有很多其它随机数产生方法，比如进位相乘法（Multiply With Carry MWC）、线性反馈移位寄存器法（Linear Feedback Shift Register,LFSR）、斐波那契LFSR（Fabonacci LFSR）、伽罗华LFSR（Galois LFSR）、Mersenne Twister（MT）等等，设计一个好的随机数发生器并不容易，还好，前面提到的几种发生器对满足一般任务还是足够了。总的来说，LCG很高效，时间空间效率均衡，MT随机性高，但相对较消耗空间。
  在这特别要说的是，在图形学中，噪声的生成与这些随机数发生器有千丝万缕的联系，选择一个好的随机数发生器将会让工作更加得心应手。

五. 常见插值方法

  当我们或者噪声值后，这些噪声值只是些离散的值，用这些插值来来填充离散值之间空隙。如果不插值，那噪声看起来是这样的（一维）。

  对离散值进行平滑处理的方式也有很多，下面我们从最简单的入手，作以介绍。

(一)线性插值

  线性插值（linear interpolation）是最简单的插值，其插值公式为：

$$l=a*t + (1-t)*b$$
  其中参数 0<= t<=1，对上图线性插值的结果如下：

  可以看到，线性插值其实是将两个点用直线直接连接起来了，所以在边界处会有明显的峰，或者说不够平滑。在某些场合下，这些锐利的峰会让处理结果非常不尽如人意。

(二)余弦插值

  余弦插值就是为了解决线性插值不平滑的问题的，余弦插值思想也非常简单，将线性插值中的 t 替换成一个余弦值。

  float Cos_Interpolate(float a, float b, float t){float ft = t * 3.1415927t = (1 - cos(ft)) * 0.5return a*t + (1-t)b}

  其中参数 0<= t<=1，对上图线性插值的结果如下：

  可以看到，经过余弦插值后，生成的曲线平滑多了，这也更符合自然规律了。

(三)Cubic 插值

  Cubic插值不叫立方体插值，而是立方插值，更直白一些就叫三次方插值，因为Cubic插值就是利用最高阶为三次方的多项式来计算插值。Cubic插值比余弦插值有更好的平滑性，其插值公式利用三次多项式及其导数：

$$f(x)=ax^3+bx^2+cx +d$$
$$f'(x)=3ax^2+2bx+c$$
在端点处的值求解参数a,b,c,d，最后得出插值公式：
$$f(p_0,p_1,p_2,p_3,x) = (-\tfrac{1}{2}p_0 + \tfrac{3}{2}p_1 - \tfrac{3}{2}p_2 + \tfrac{1}{2}p_3)x^3 + (p_0 - \tfrac{5}{2}p_1 + 2p_2 - \tfrac{1}{2}p_3)x^2 + (-\tfrac{1}{2}p_0 + \tfrac{1}{2}p_2)x + p_1$$
从上面的表达式可以看出，Cubic插值需要四个参数来确定一个值，即利用四个点来做插值计算，如果要在边界处插值就需要定义额外的点来模拟了，简单的做法就是在端点处，让v’(0) = v(0)和v’(3) = v(3),或者将端点视为额外点与端点后一点（前一点）的中点，即v(0)=1/2(v’(0)+v(2))，v(3)=1/2(v(2)+v’(3))，得出v’(0)=2v(0)-v(2)，v’(3)=2v(3)-v(2)。知道公式了，Cubic插值算法就简单了：

float Cubic_Interpolate(float v0, float v1, float v2, float v3, float t)
{return  v0 + 0.5 * t*(v2 - v0 + x*(2.0*v0 - 5.0*v1 + 4.0*v2 - v3 + x*(3.0*(v1 - v2) + v3 - v0)));
}

效果如下，比余弦插值更平滑了。

(四)Hermite插值

  Hermite插值是我们最熟悉的陌生插值算法，熟悉是smoothstep就是采用的Hermite插值来做计算的（采用了优化版本），三次Hermite插值公式是 :

$$f(t) = (2*t^3 - 3*t^2 + 1)v0 + (t^3 - 2*t^2 + t)m0 + (t^3 - t^2)m1 + (-2*t^3 + 3*t^2)v1$$
  其中v0，v1是两个端点，m0是v0点处的方向，m1是v1处的方向,或者说是插值后平滑曲线在v0,v1处的切向量，即m0=v1-v0,m1=v3-v2，参数t从0变化到1的过程中f(t)形成的轨迹构成了从v0到v1的平滑曲线，m0,m1的大小会影响到曲线的形状。

float Hermite_Interpolate(float v0, float m0, float v1, float m1, float t)
{return  v0 + t*(m0 + t*(-3v0 - 2m0 - m1 + 3v1 + t*(2v0 + m0 + m1 - 2v1)));
}

(五)Sphere 插值

  Sphere插值往往跟四元数插值相关，用来在两个四元数之间进行平滑插值以达到动画平滑的目的。Sphere插值原理也很简单，但需要注意处理小角度和正反旋转的问题。其C++代码如下：

private  Quternion LerpAndNormalize(Quternion p,Quternion q, float t)
{return Normalize((1.0f-t)*p+t*q);
}
public Quternion Slerp(Quternion p,Quternion q, float t) 
{if(Length(p-q) > Length(p+q))  q=-q;float cosphi = DotP(p,q);if(cosphi > (1.0f - 0.001))return LerpAndNormalize(p,q,t);float phi = (float)Math.Acos(cosphi);float sinphi =(float)Math.Sin(phi);return ((float)Math.Sin(phi*(1.0f - t)/sinphi)*p + ((float)Math.Sin(phi*t)/sinphi)*q;
}

六. 小结

  本篇文章是这个系列的开篇，简单的介绍了噪声，主要引入了随机数和插值，这些最基本的操作在接下来的噪声生成过程中将扮演十分重要的角色，理解这些基本的元素有助于其他工作的展开。

参考文献：
1、百度百科 图像噪声
2、【数字图像处理学习笔记之一】数字图像噪声 http://blog.csdn.net/zhougynui/article/details/51764798
3、Hash without Sine https://www.shadertoy.com/view/4djSRW