小蓝本 第一本 《因式分解技巧》 第七章 综合运用 笔记 (第七天)
- 前言
- 换元法
- 好题
- 例2
- 题目
- 解法
- 经验
- 补充
- 例3
- 题目
- 解法
- 经验
- 例5
- 题目
- 解法
- 补充
- 例9
- 题目
- 解法
- 经验
- 补充
- 例10
- 题目
- 解法
- 补充
- 例11
- 题目
- 解法
- 补充
- 例13
- 题目
- 解法
- 习题7
- 题目
- 题解
- 错题
- 题号
- 改错
前言
12天攻掉《因式分解技巧》的计划,已经过半,今天主要是对前6章的提升,主要讲一下第七章的题目。
我写的因式分解技巧专栏
换元法
概念
换元法就是在我们之前章中提到的观察式子整体结构把其中的一个式子看成一个字母的意识,化简后在代入
目的 : 简化运算复杂度
建议 : 这个意识真的很重要
好题
例2
题目
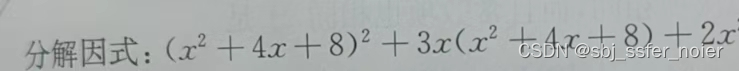
解法
- 把x2+4x+8x^2+4x+8x2+4x+8看成一个整体
- 套用模板十字相乘,如下图:
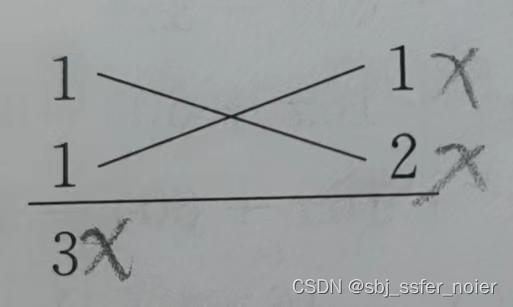
- 由此可得原式=(x2+5x+8)(x2+6x+8)原式 = (x^2+5x+8)(x^2+6x+8)原式=(x2+5x+8)(x2+6x+8)
- 在对x2+6x+8x^2+6x+8x2+6x+8进行十字相乘化简, 可得原式=(x+2)(x+4)(x2+5x+8)原式=(x+2)(x+4)(x^2+5x+8)原式=(x+2)(x+4)(x2+5x+8)
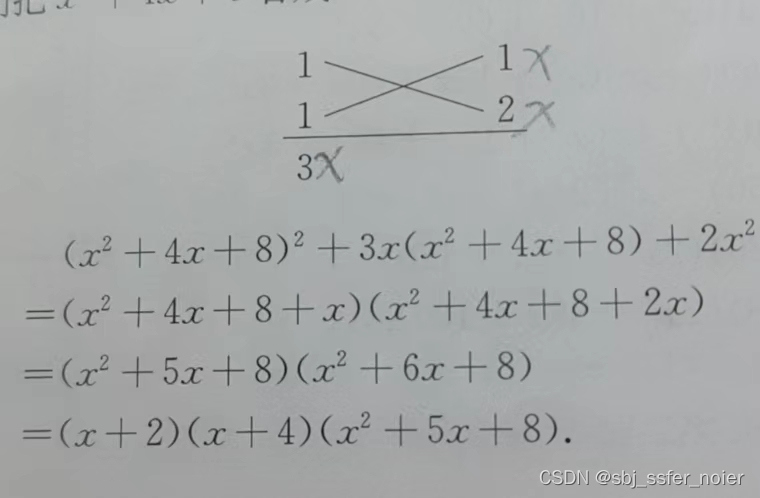
经验
善于使用换元法
补充
(x2+5x+8)(x^2+5x+8)(x2+5x+8)在有理数集内不能分解,期待第11章求根公式部分
例3
题目

解法
- 设这4个整数分别是 x+1x+1x+1、x+2x+2x+2、x+3x+3x+3、x+4x+4x+4
- 根据题目可得式子(x+1)(x+2)(x+3)(x+4)+1(x+1)(x+2)(x+3)(x+4)+1(x+1)(x+2)(x+3)(x+4)+1,最终就是将他因式分解看是不是平方数
- 不难发现(x+1)(x+4)(x+1)(x+4)(x+1)(x+4)和(x+2)(x+3)(x+2)(x+3)(x+2)(x+3)二次项和一次项系数都相同,将他们相互乘起来
- 得新式(x2+5x+4)(x2+5x+6)+1(x^2+5x+4)(x^2+5x+6)+1(x2+5x+4)(x2+5x+6)+1
- 把(x2+5x+4)(x^2+5x+4)(x2+5x+4)与(x2+5x+6)(x^2+5x+6)(x2+5x+6),分别看成他们得平均数±n±n±n
- 得新式(x2+5x+5−1)(x2+5x+5+1)+1(x^2+5x+5-1)(x^2+5x+5+1)+1(x2+5x+5−1)(x2+5x+5+1)+1
- 根据平方差公式反推出新式(x2+5x+5)2−1+1(x^2+5x+5)^2-1+1(x2+5x+5)2−1+1
- 化简得(x2+5x+5)2(x^2+5x+5)^2(x2+5x+5)2
- 得证

经验
反向十字相乘观察式子得规律性
例5
题目
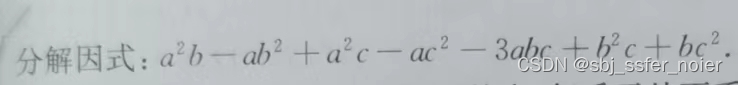
解法
- 关于a、b、c的多项式,有这么多项组成。这种问题抓一个对象进行降幂排列
- 抓a进行降幂排列,得式子(b+c)a2−(b2+c2+3bc)a+(b2c+bc2)(b+c)a^2-(b^2+c^2+3bc)a+(b^2c+bc^2)(b+c)a2−(b2+c2+3bc)a+(b2c+bc2)
- 对这里的"常数项"提公因式,得新式(b+c)a2−(b2+c2+3bc)a+bc(b+c)(b+c)a^2-(b^2+c^2+3bc)a+bc(b+c)(b+c)a2−(b2+c2+3bc)a+bc(b+c)
- 套用十字相乘模板,如下图:
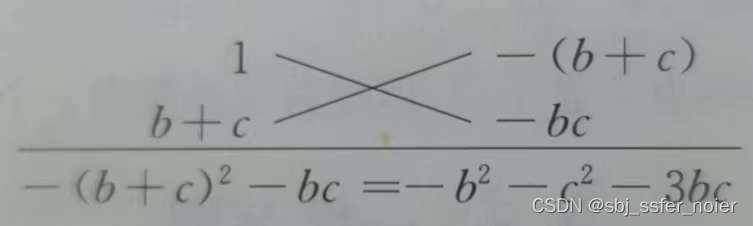
- 得新式,(a−b−c)(ab+ac−bc)(a-b-c)(ab+ac-bc)(a−b−c)(ab+ac−bc)
补充
10.4章例11还有另一种解法
例9
题目
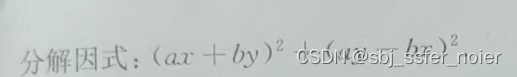
解法
- 这种情况不能继续分解,将式子展开处理,得新式a2x2+2abxy+b2y2+a2y2−2abxy+b2x2a^2x^2+2abxy+b^2y^2+a^2y^2-2abxy+b^2x^2a2x2+2abxy+b2y2+a2y2−2abxy+b2x2
- 继续化简得a2x2+b2y2+a2y2+b2x2a^2x^2+b^2y^2+a^2y^2+b^2x^2a2x2+b2y2+a2y2+b2x2
- 最终提取2次公因式,得(a2+b2)(x2+y2)(a^2+b^2)(x^2+y^2)(a2+b2)(x2+y2)

经验
完全平方和与完全平方差的互补效应
补充
等式表明了2个平方和的积还是平方和
例10
题目
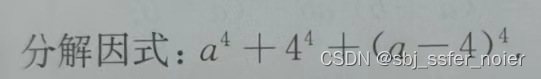
解法
- 为了式子更加对称,设x=a−2x=a-2x=a−2
- 新式为,(x+2)4+44+(x−2)4(x+2)^4+4^4+(x-2)^4(x+2)4+44+(x−2)4
- 分别应用完全平方和与完全平方差公式,推出式子为:(x2+4x+4)2+(x2−4x+4)2+44(x^2+4x+4)^2+(x^2-4x+4)^2+4^4(x2+4x+4)2+(x2−4x+4)2+44
- 在应用完全平方和与完全平方差公式,得新式:(x4+16x2+16+8x3+8x2+32x)+(x4+16x2+16−8x3+8x2−32x)+44(x^4+16x^2+16+8x^3+8x^2+32x)+(x^4+16x^2+16-8x^3+8x^2-32x)+4^4(x4+16x2+16+8x3+8x2+32x)+(x4+16x2+16−8x3+8x2−32x)+44
- 进一步化简:2(x4+24x2+16)+2562(x^4+24x^2+16)+2562(x4+24x2+16)+256
- 2(x2+24x2+144)2(x^2+24x^2+144)2(x2+24x2+144)
- 2(x2+12)22(x^2+12)^22(x2+12)2
- 带入x,2(a2−4a+16)22(a^2-4a+16)^22(a2−4a+16)2

换元法
补充
第11章例12的特殊情况
例11
题目
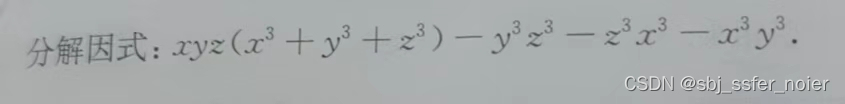
解法
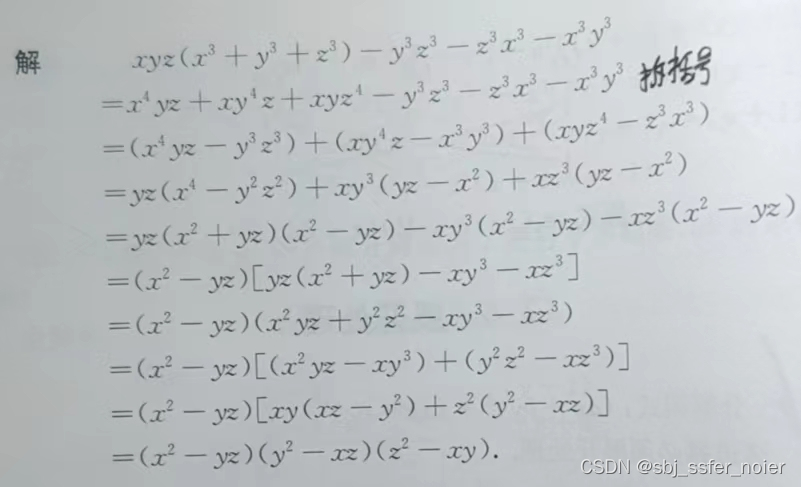
补充

例13
题目

解法

习题7
题目

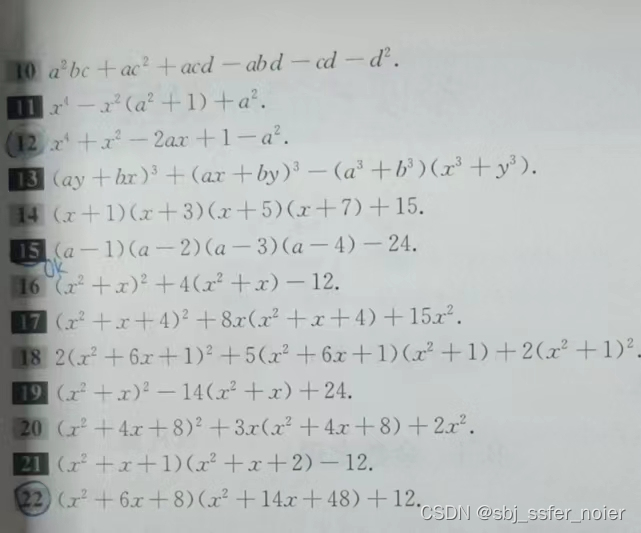
题解



错题
题号
5 6 12 15 22
改错