前言

本文章一部分内容参考于《代码随想录》----如有侵权请联系作者删除即可，撰写本文章主要目的在于记录自己学习体会并分享给大家，全篇并不仅仅是复制粘贴，更多的是加入了自己的思考，希望读完此篇文章能真正帮助到您！！！

算法题（LeetCode刷题59螺旋矩阵II）—（保姆级别讲解）

力扣题目链接

分析题目：

1. 元素按照顺时针顺序螺旋排列的正方形矩阵
2. 正方形：就需要保证每一边的长度是不变的
3. 遍历过程需要保证循环不变量原则

算法思想（重要）

1. 什么是循环不变量原则？
   在之前的二分查找中我们就已经运用了循环不变量原则，在这里再提一下：由于在本篇中我们要遍历螺旋矩阵，也就意味着同样一个点不需要重复遍历很多次，所以为了避免这个情况，我们将遍历每条边的规则确定下来，即在本篇中使用左闭右开的规则，这样就可以成功解决问题。
2. 在本篇中我们需要给定一个正整数n，那么这个正整数有什么作用呢？
   正整数n一共分为两种情况，分别是奇数和偶数。这里举个例子，假设n为奇数，即n = 3，那么最终输出结果应该为[ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]，所以我们需要通过这个参数n来确定我们一共需要循环遍历几圈，只不过每圈遍历的规则是一样的。在本篇中循环几圈可以通过n/2确定。
3. 假设我们现在在循环遍历第一圈，即可以将完整的一圈分为四种情况，分别是上，右，下，左。以上为例，由于我们采取左闭右开的规则，所以最后一个节点是下一次遍历的开始节点，以此类推。

螺旋矩阵II代码：

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n, 0)); int startx = 0, starty = 0; int loop = n / 2; int mid = n / 2; int count = 1; int offset = 1; int i,j;while (loop --) {i = startx;j = starty;for (j = starty; j < n - offset; j++) {res[startx][j] = count++;}for (i = startx; i < n - offset; i++) {res[i][j] = count++;}for (; j > starty; j--) {res[i][j] = count++;}for (; i > startx; i--) {res[i][j] = count++;}startx++;starty++;offset += 1;}if (n % 2) {res[mid][mid] = count;}return res;}
};

时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
空间复杂度 O(1)

我们还是老样子，对代码逐句进行分析：

 vector<vector<int>> res(n, vector<int>(n, 0)); 

//使用vector定义一个二维数组

int startx = 0, starty = 0; 

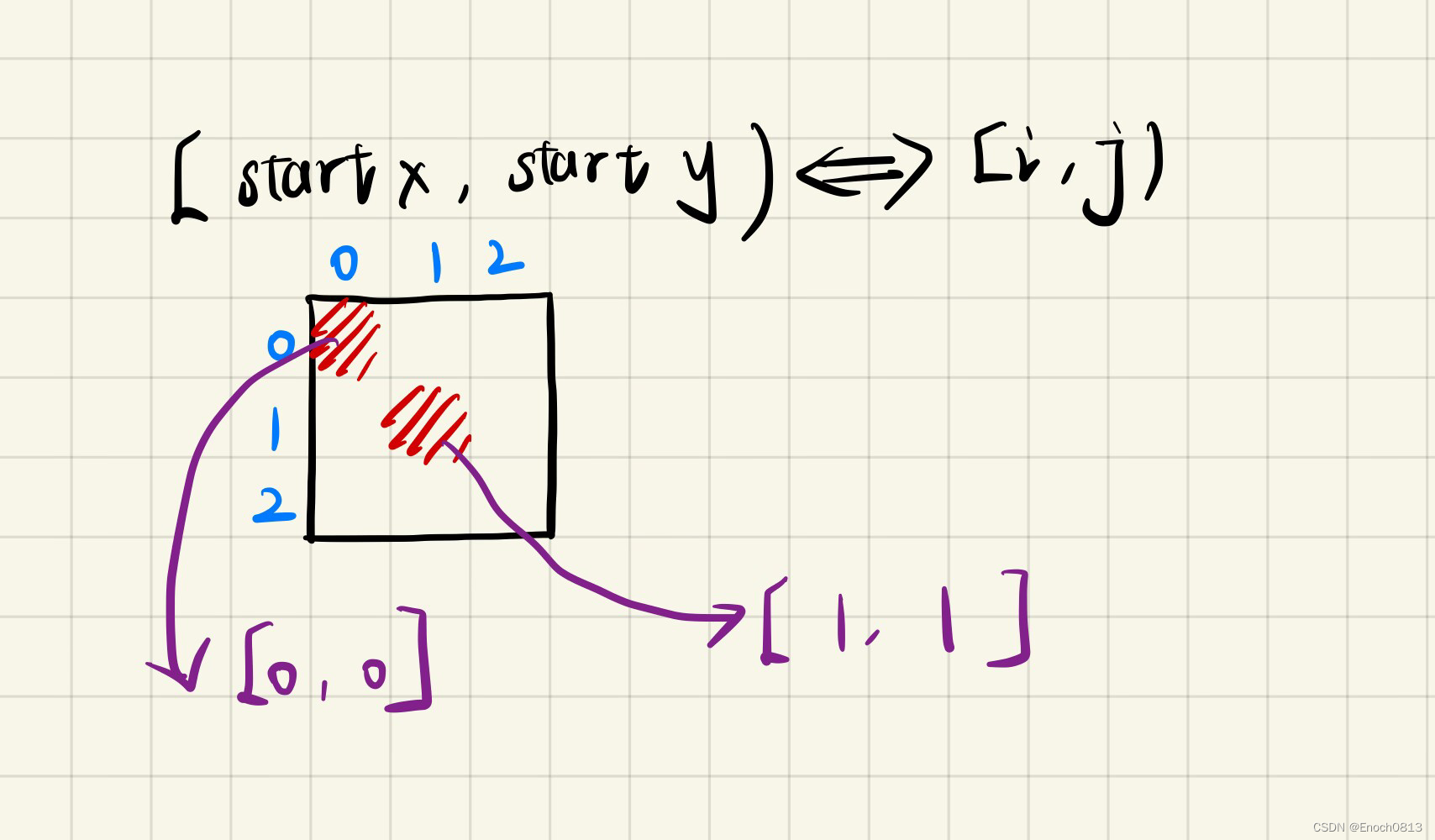
 int loop = n / 2; 

//相当于是确定了遍历螺旋矩阵需要循环的圈数。例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理。假设n为偶数4，那么loop = 2就循环两圈，也就相当于矩阵没有需要单独处理的中间值。

int mid = n / 2; 

//相当于是n为奇数就会遗留出中间值的情况，所以mid相当于是矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)

int count = 1; 

这里count = 1 相当于第一个数为1，一次递增即可。

int offset = 1; 

// 需要控制每一条边遍历的长度，每次循环右边界收缩一位

while (loop --) 

//前面已经提过总共循环的圈数。

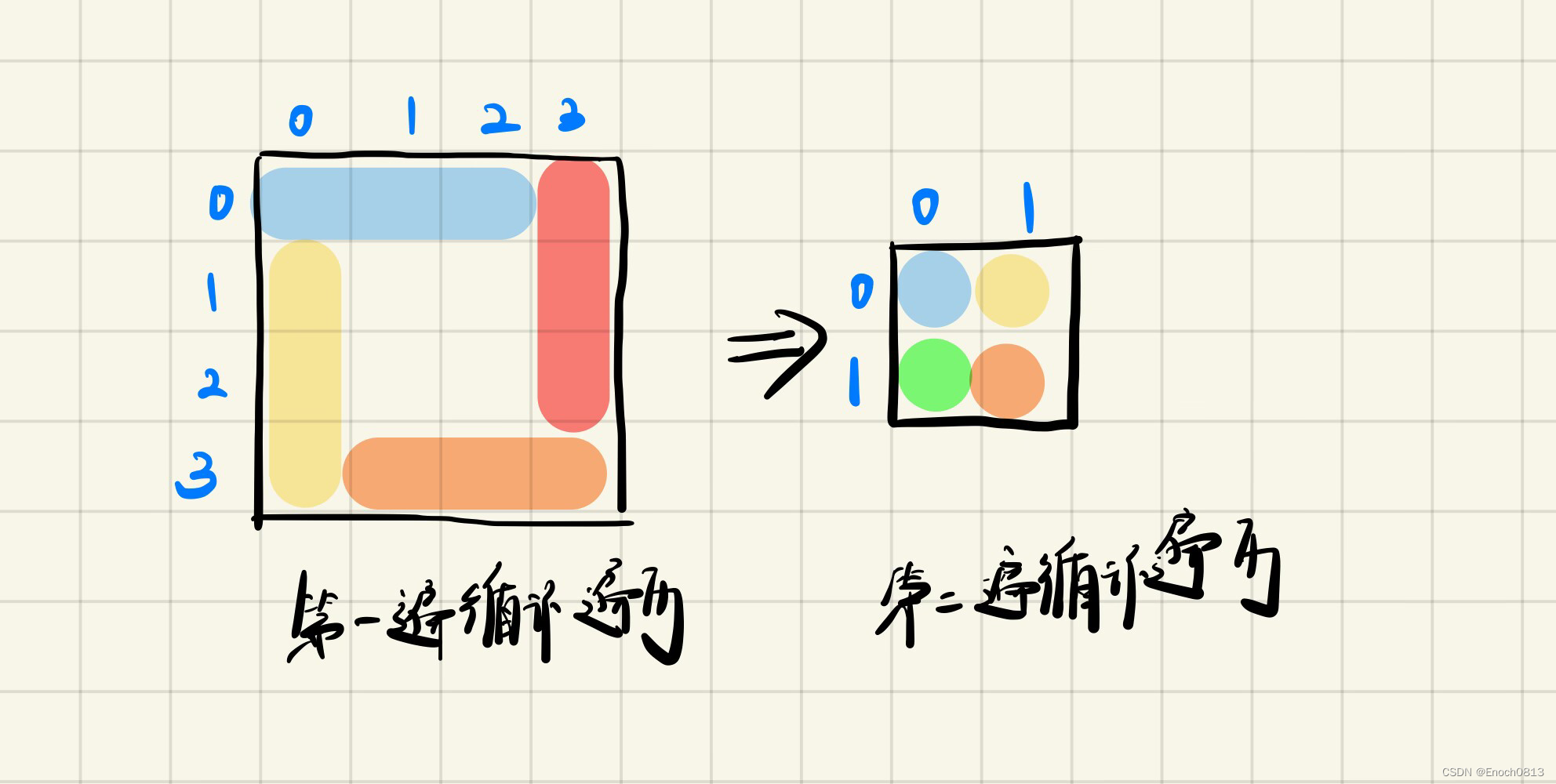
for (j = starty; j < n - offset; j++) {res[startx][j] = count++;}

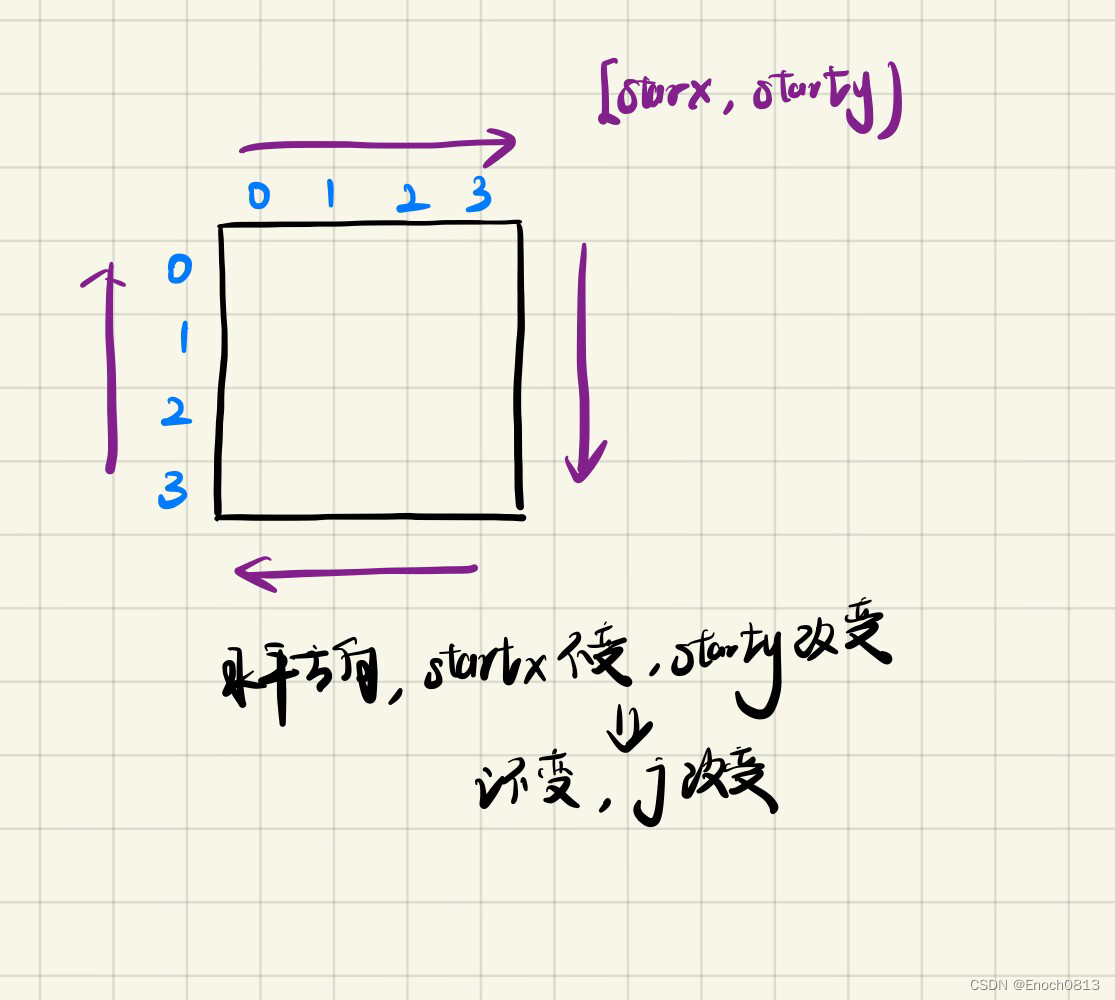
//初始化offest为1，由于遵循左闭右开的原则，所以是j < n - offset，即第一圈为j < n - 1，如上图所示为j的范围为[0,3)

for (i = startx; i < n - offset; i++) {res[i][j] = count++;}

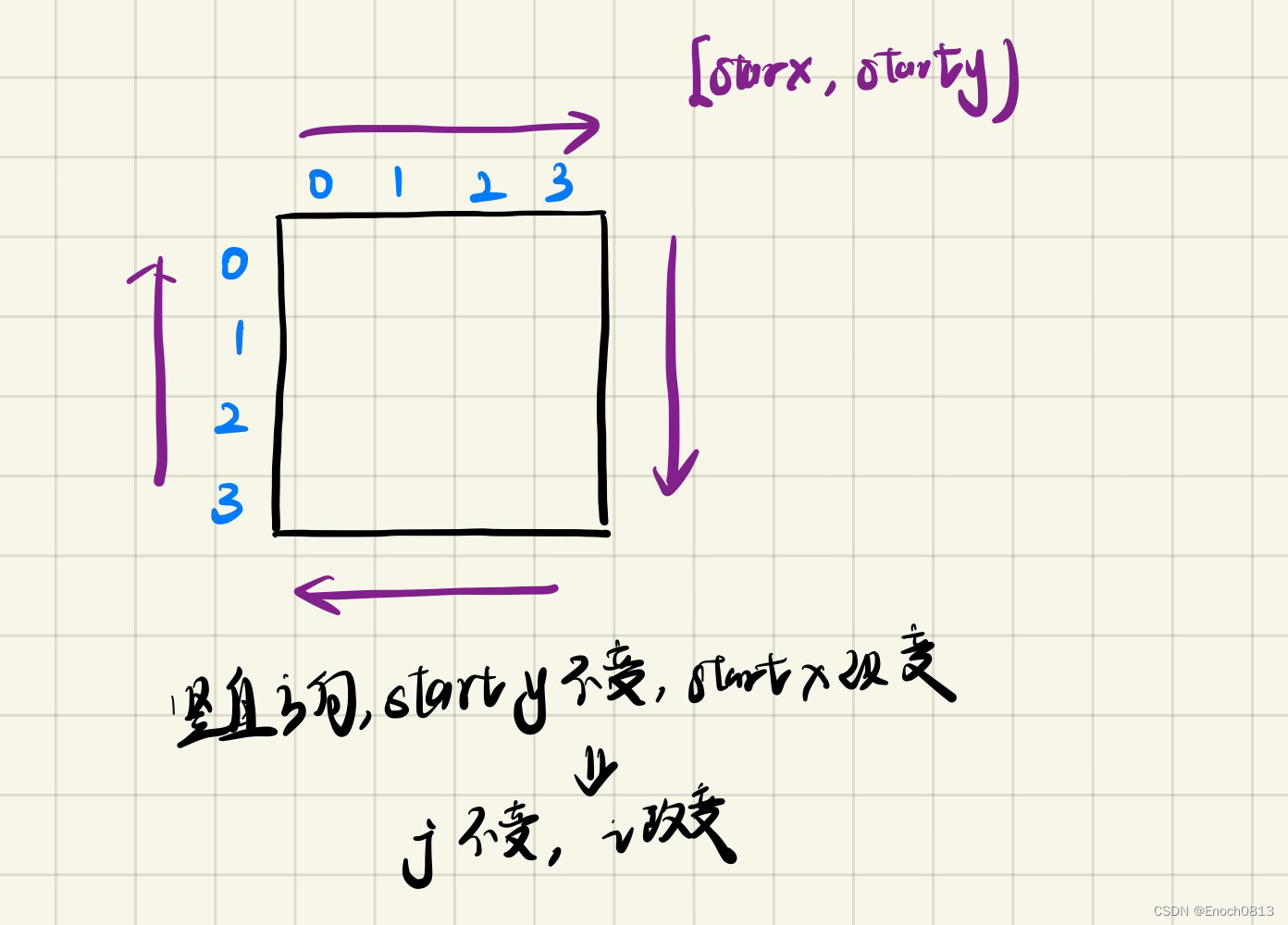
初始化offest为1，由于遵循左闭右开的原则，所以是i < n - offset，即第一圈为i < n - 1，如上图所示为i的范围为[0,3),并且此时j的值已经为n - offest，所以直接为j即可。

for (; j > starty; j--) {res[i][j] = count++;}

//由于此时j的值已经为最大值，即n - offset，所以就没必要对j进行初始化。并且此时starty 为0

 for (; i > startx; i--) {res[i][j] = count++;}

//由于此时i的值已经为最大值，即n - offset，所以就没必要对i进行初始化。并且此时startx 为0

 startx++;starty++;

//第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)

 offset += 1;

//offset 控制每一圈里每一条边遍历的长度

if (n % 2) {res[mid][mid] = count;}

//如果n为奇数的话，需要单独给矩阵最中间的位置赋值

结束语

如果觉得这篇文章还不错的话，记得点赞 ，支持下！！！