前缀和

输入一个长度为 n的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r

对于每个询问，输出原序列中从第 l 个数到第 r个数的和。

输入格式第一行包含两个整数 n和 m

第二行包含 n个整数，表示整数数列。

接下来 m行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式共 m 行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n ,
1≤n,m≤100000 ,
−1000≤数列中元素的值≤1000

输入样例：

输出样例：

3
6
10

前缀和的用处：前缀和数组能以On(1)的方式求出给定范围内数组的和。

在很多地方都用的上前缀和数组，只是它很容易被人忽略，所以得多练练加深印象。

解题思路：本题是一维数组的前缀和，思路很简单，直接在原数组上进行修改即可。

求前缀和数组：设原数组为a[],我们可知递推方程为a[i]=a[i-1]+a[i]

前缀和数组求出后，要知道给定范围内[i,j]的数组和，就很简单了
方程为 vla=a[j]-a[i-1]

代码：

#include<iostream>using namespace std;const int N=100010;
int a[N];
int b[N];int main()
{int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) a[i]=a[i-1]+a[i];while(m--){int l,r;scanf("%d%d",&l,&r);cout<<a[r]-a[l-1]<<endl;}
}

子矩阵的和

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n，m，q

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q行，每行输出一个询问的结果。

数据范围：

1≤n,m≤1000
,
1≤q≤200000
,
1≤x1≤x2≤n
,
1≤y1≤y2≤m
,
−1000≤矩阵内元素的值≤1000

输入样例：

输出样例：

17
27
21

本题大致意思同上题差不多，只是从一维数组变为二维数组，有些不太好理解；

要求给定范围内的数组和，先说求二维前缀和的递推公式

a[i][j]=a[i][j-1]+a[i-1][j]-a[i-1][j-1]+a[i][j];

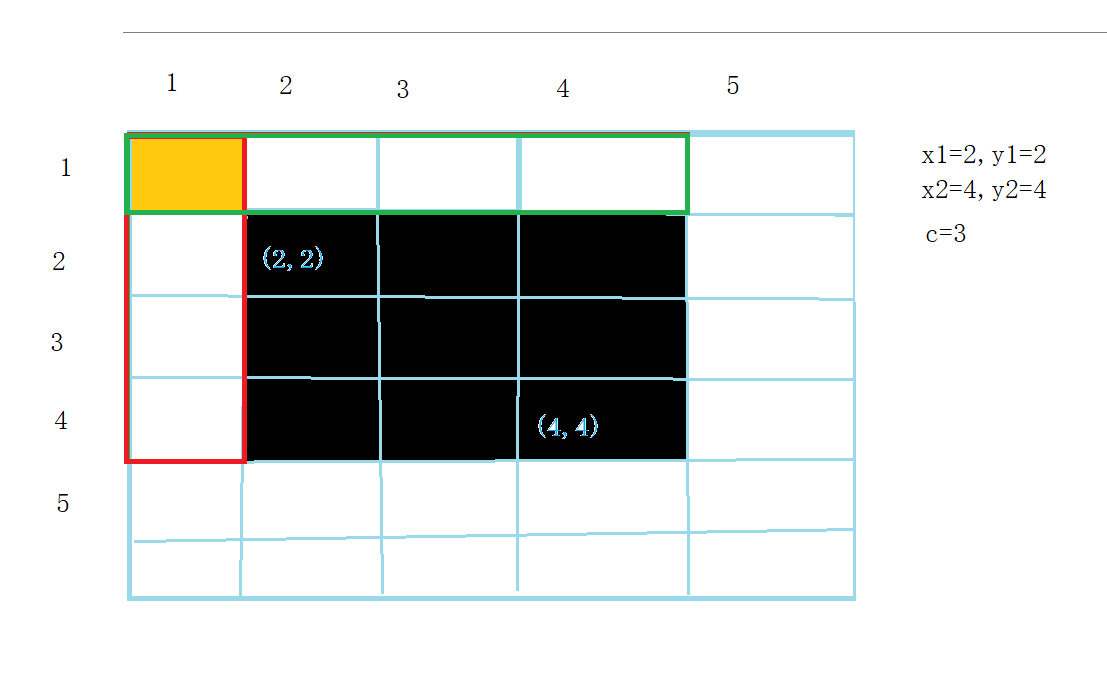
在这里插入图片描述

看图：
黑颜色即为所求，但是当我们在减去多余部分的时候，有一块区域会被减去两次，如上图，就是橙色的区域，因此我们需要将其加回来。
代码：

#include<iostream>using namespace std;const int N=1010;
int a[N][N];int main()
{int n,m,q;scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){a[i][j]=a[i][j-1]+a[i-1][j]-a[i-1][j-1]+a[i][j];}}while(q--){int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);int val=a[x2][y2]-a[x2][y1-1]-a[x1-1][y2]+a[x1-1][y1-1];cout<<val<<endl;}return 0;
}