前言

相比于D1T1，这题才是真正的签到题，然而，我却爆0了。为了纪念这悲壮的0分，写下了这篇题解。

题目大意

给出 $n(1\le n\le 10^5)$ 个字符串及其出现时间（以几点几分给出），每个字符串会存在 $m(1\le m\le 1440)$ 个单位时间（分钟），求存在字符串最多的时间点有多少个字符串（注意：同个字符串在同一时间点重叠只算一个字符串）

解题思路

实际上，最麻烦的地方是相同会出现重叠，并且不管重叠几次，都只造成 $1$ 的贡献。所以，显而易见，我们需要将每一个字符串分开考虑。参考下图：

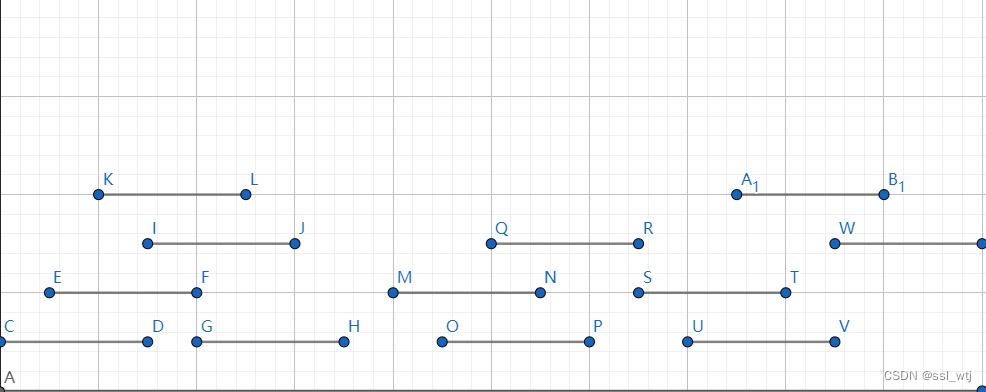
由于重叠部分也只造成 $1$ 的贡献，我们考虑进行区间合并。先按照左端点排序：

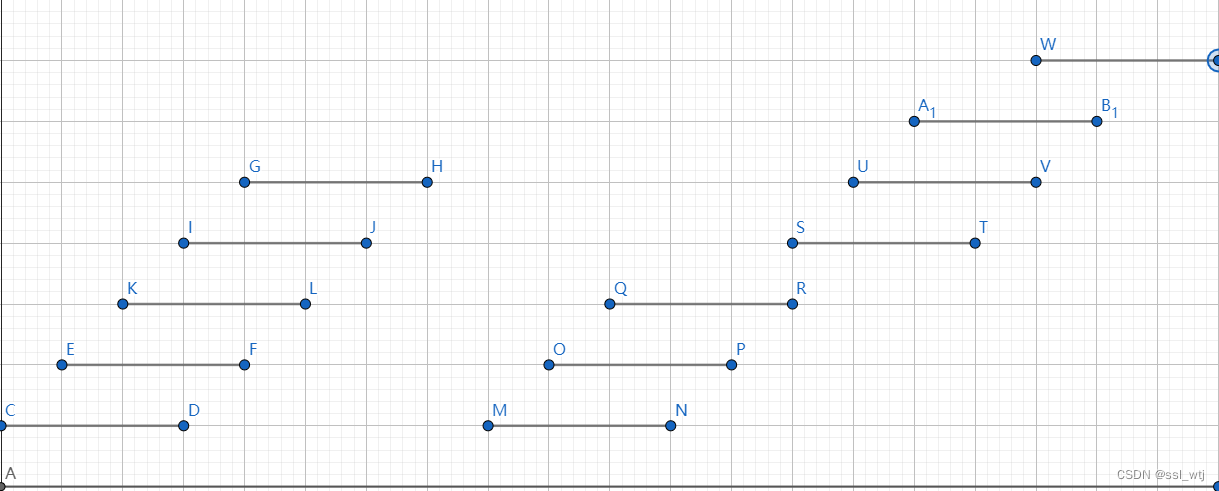
如果下一个区间的左端点小于这一个区间的右端点，那么一定可以进行区间合并，也就是将右端点后移，合并后，得到下图：

再进行区间加即可。相信大家第一个想到的都是差分，可是从这里开始，我突然脑抽了，果断打起了线段树，过了样例（因为太水了……），然后爆0了。赛后调出来了，写篇题解给自己一个警告：就算再喜欢线段树，考场上也尽量不要写！！！

代码实现

#include <bits/stdc++.h>
using namespace std;
struct node {long long l, r, laz, Max;
} segment_tre[10010];
struct node2 {long long f, t;
};
long long n, m, tot;
unordered_map<string, long long> mem;
vector<node2> v[100010], sorted_v[100010];
string s1, s2;
void setup(long long i, long long l, long long r) {segment_tre[i].l = l;segment_tre[i].r = r;if (l == r)return;long long mid = ((l + r) >> 1);setup(i * 2, l, mid);setup(i * 2 + 1, mid + 1, r);
}
void push_d(long long i) {if (segment_tre[i].laz != 0) {segment_tre[i * 2].Max += segment_tre[i].laz;segment_tre[i * 2].laz += segment_tre[i].laz;segment_tre[i * 2 + 1].Max += segment_tre[i].laz;segment_tre[i * 2 + 1].laz += segment_tre[i].laz;segment_tre[i].laz = 0;}return;
}
void change(long long i, long long l, long long r, long long num) {if (segment_tre[i].l >= l && segment_tre[i].r <= r) {segment_tre[i].laz++;segment_tre[i].Max++;return;}push_d(i);if (segment_tre[i * 2].r >= l)change(i * 2, l, r, num);if (segment_tre[i * 2 + 1].l <= r)change(i * 2 + 1, l, r, num);segment_tre[i].Max = max(segment_tre[i * 2].Max, segment_tre[i * 2 + 1].Max);return;
}
long long ask(long long i, long long l, long long r) {if (segment_tre[i].l >= l && segment_tre[i].r <= r)return segment_tre[i].Max;push_d(i);long long value = 0;if (segment_tre[i * 2].r >= l)value = max(value, ask(i * 2, l, r));if (segment_tre[i * 2 + 1].l <= r)value = max(value, ask(i * 2 + 1, l, r));return value;
}
long long work(string s) { return ((s[0] - '0') * 10 + s[1] - '0') * 60 + (s[3] - '0') * 10 + s[4] - '0'; }
int main() {ios::sync_with_stdio(false);cin.tie(0);freopen("switch.in", "r", stdin);freopen("switch.out", "w", stdout);cin >> n >> m;setup(1, 0, 24 * 60);for (int i = 1; i <= n; i++) {cin >> s1 >> s2;if (mem[s1] == 0) {mem[s1] = ++tot;v[tot].push_back((node2){ work(s2), work(s2) + m - 1 });} elsev[mem[s1]].push_back((node2){ work(s2), work(s2) + m - 1 });}for (int i = 1; i <= tot; i++) {sort(v[i].begin(), v[i].end(), [&](node2 q, node2 h) -> bool { return q.f < h.f; });long long f = v[i][0].f, t = v[i][0].t;for (int j = 1; j < v[i].size(); j++)if (v[i][j].f <= t)t = v[i][j].t;else {sorted_v[i].push_back((node2){ f, t });f = v[i][j].f;t = v[i][j].t;}sorted_v[i].push_back((node2){ f, t });}for (int i = 1; i <= tot; i++)for (int j = 0; j < sorted_v[i].size(); j++) change(1, sorted_v[i][j].f, sorted_v[i][j].t, 1);cout << ask(1, 0, 24 * 60);return 0;
}