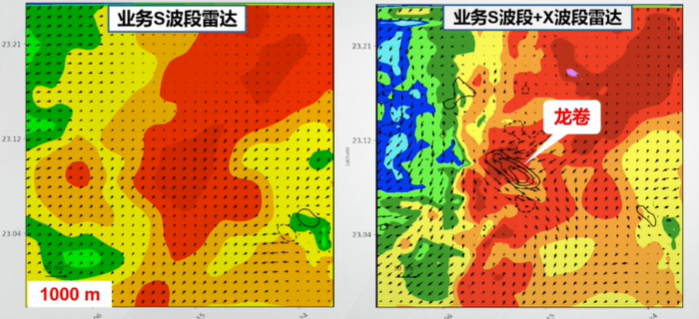
说起小波变换就需要提起傅里叶变换。傅里叶变换就是把波进行分解，可以认为任意一个周期波都可以有足够多的正弦（余弦）波组成，这里足够多的正弦波对应的频率不同，把这些足够的正弦波放在频域中，就是傅里叶变换，详细傅里叶变换可以参见这里，如图1。

详细的小波变换可以参考这里，简单说来就是用一系列集中的、能量有限的波代替正弦波。而Haar小波变换就是利用haar滤波器进行计算。

一维Haar 变换计算如下：

设原始一维数据 ,   Haar低通滤波 [1, 1] , Haar高通滤波[-1, 1], 

则Haar小波变换为：， 当需要进行下2采样时计算其均值（也有保留偶数序列），直接取

再次进行小波变换：， 下2采样为 c1 。将 称为细节系数。因此通过Haar 变换，一幅分辨率为4的数据就可以由分辨率为1，以及3个细节系数表示。同样由降采样的数据和细节系数可以恢复出原始数据。从上面计算过程可以看出：矢量a 与低通滤波器卷积得到近似，与高通滤波器卷积得到细节

二维图像Haar变换：

对于二维图像Haar变换不再从一个方向进行滤波，而是从水平和竖直两个方向进行低通和高通滤波（水平和竖直先后不影响），用图像表述如图2所示：图2中a表示原图，图b表示经过一级小波变换的结果，h1 表示水平反向的细节，v1 表示竖直方向的细节，c1表示对角线方向的细节，b表示下2采样的图像。图c中表示继续进行Haar小波变换。一级Haar小波变换实际效果如图3所示