激活函数
- 1- SIgmoid
- 1-1 sigmoid导数
- 2- tanh
- 2-1 tanh函数导数
- 3- ReLU
- 4- LeakyReLu
- 5- LR 公式推导
Sigmoid、tanh、ReLU、LeakyReLu
1- SIgmoid
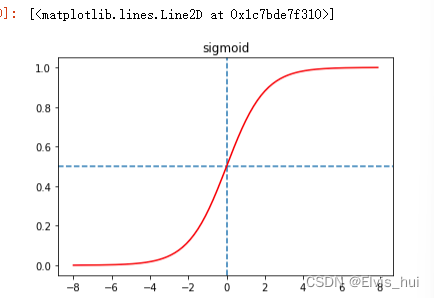
sigmoid 函数将元素的值映射到0和1之间
sigmoid(x)=11+exp(−x)sigmoid(x)=\frac{1}{1+exp(-x)}sigmoid(x)=1+exp(−x)1
import torch
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.sigmoid()
plt.title('sigmoid')
plt.axhline(0.5,ls='--')#画横线
plt.axvline(0,ls='--')#画竖线
plt.plot(x.detach(), y.detach(),'red')
1-1 sigmoid导数
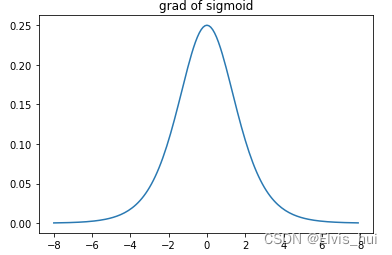
sigmoid′(x)=sigmoid(x)(1−sigmoid(x))sigmoid^{'}(x)=sigmoid(x)(1-sigmoid(x))sigmoid′(x)=sigmoid(x)(1−sigmoid(x))
绘制sigmoid函数的导数。当输入为0时,sigmoid函数的导数达到最大值0.25;当输入越偏离0时,sigmoid函数的导数越接近0
sigmoid斜率图
import torch
import matplotlib.pyplot as pltx = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.sigmoid()
x.grad = torch.zeros_like(x)#创建一个与x形状相同的全零张量,并将其赋值给x.grad属性,以便在之后的backward()计算中重新计算梯度。
y.sum().backward()
plt.plot(x.detach().numpy(), x.grad.detach().numpy())
plt.title('grad of sigmoid')
plt.show()
2- tanh
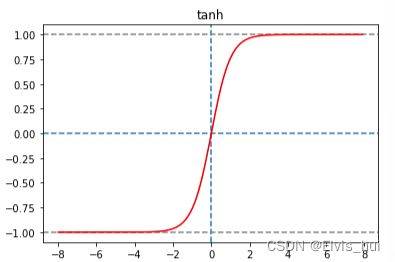
tanh(双曲正切)函数可以将元素的值变换到-1和1之间 ,阈值(-1,1)
tanh(x)=1−exp(−2x)1+exp(−2x)=ez−e−zez+e−ztanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)}=\frac{e^z-e^{-z}}{e^z+e^{-z}}tanh(x)=1+exp(−2x)1−exp(−2x)=ez+e−zez−e−z
函数图像
y = x.tanh()
plt.title('tanh')
plt.axvline(0,ls='--')
plt.axhline(0,ls='--')
plt.axhline(1,ls='--',c='gray')
plt.axhline(-1,ls='--',c='gray')
plt.plot(x.detach(), y.detach(),'red')
2-1 tanh函数导数
tanh′(x)=1−tanh2(x)tanh'(x)=1-tanh^2(x)tanh′(x)=1−tanh2(x)
y = x.tanh()
x.grad.zero_()
y.sum().backward()
plt.title('grad of tanh')
plt.plot(x.detach().numpy(), x.grad.detach().numpy())
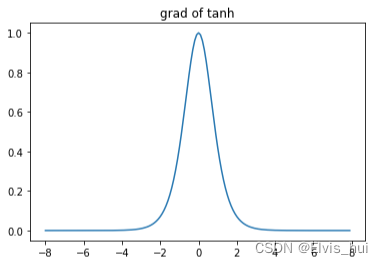
σ和tanh有一个缺点,那就是z非常大或是非常小的时候,那么导数的梯度或者说这个函数的斜率就很小,拖慢梯度学习算法,造成梯度消失
3- ReLU
非线性激活函数,被称为修正线性单元
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.relu()
plt.title('relu')
plt.plot(x.detach(), y.detach(),c='red')
plt.axvline(0,ls='--')
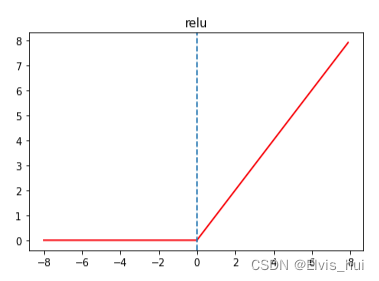
给定元素x,该函数定义为:ReLU(x)=max(x,0)x,该函数定义为:ReLU(x)=max(x,0)x,该函数定义为:ReLU(x)=max(x,0)
显然,当输入为负数时,ReLU函数的导数为0;当输入为正数时,ReLU函数的导数为1。尽管输入为0时ReLU函数不可导,但是我们可以取此处的导数为0
4- LeakyReLu
f(x)=max(αx,x)f(x) = max(\alpha x, x)f(x)=max(αx,x)
def ReakyReLU(x, alpha=0.01):return np.where(x < 0, alpha * x, x)y=ReakyReLU(x.detach().numpy())
plt.plot(x.detach().numpy(),y)
plt.axhline(0,c='grey')
plt.title('ReakyReLU function')
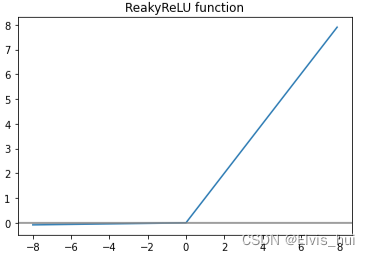
LeakyReLu:g(z)=max(0.001z,z),g′(z)=[0.01ifz<0else1]Leaky ReLu:g(z)=max(0.001z,z), \\ g^{'}(z)=[0.01 \space if \space z<0\space else\space 1]LeakyReLu:g(z)=max(0.001z,z),g′(z)=[0.01 if z<0 else 1]
其中,α\alphaα是一个小的正数,通常取0.01。与ReLU函数不同的是,当输入值小于0时,Leaky ReLU函数输出的是输入值的一个小的比例,而不是0。这样可以避免ReLU函数在输入为负时出现死亡神经元的问题,提高了模型的稳定性和泛化性能。
Summary
sigmoid:g′(z)=a(1−a)tanh:g′(z)=1−tanh2(z)=1−a2ReLu:g(z)=max(0,z),g′(z)=[0ifz<0else1]LeakyReLu:g(z)=max(0.001z,z),g′(z)=[0.01ifz<0else1]\\sigmoid:g^{'}(z)=a(1-a)\\ tanh: g^{'}(z)=1-tanh^{2}(z)=1-a^2\\ ReLu:g(z)=max(0,z) ,g^{'}(z)=[0 \space if \space z<0\space else\space 1]\\ Leaky ReLu:g(z)=max(0.001z,z),g^{'}(z)=[0.01 \space if \space z<0\space else\space 1]sigmoid:g′(z)=a(1−a)tanh:g′(z)=1−tanh2(z)=1−a2ReLu:g(z)=max(0,z),g′(z)=[0 if z<0 else 1]LeakyReLu:g(z)=max(0.001z,z),g′(z)=[0.01 if z<0 else 1]
5- LR 公式推导
repeat some operations ,update the parameter weight and bais for the loss fun
z=wTx+bz=w^Tx+bz=wTx+b
y^=a=σ(z)=11+e−z\hat y=a =σ(z)=\frac{1}{1+e^{-z}}y^=a=σ(z)=1+e−z1
损失函数
L(a,y)=−(ylog(a)+(1−y)log(1−a))L(a,y)=-(ylog(a)+(1-y)log(1-a))L(a,y)=−(ylog(a)+(1−y)log(1−a))
通过链式求导法则求出参数-单个训练样本
求偏导
da=∂L∂a=−ya+1−y1−ada=\frac{\partial L}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}da=∂a∂L=−ay+1−a1−y
dz=∂L∂z=∂L∂a∗∂a∂z=∂L∂a∗a(1−a)=a−ydz=\frac{\partial L}{\partial z}= \frac{\partial L}{\partial a}*\frac{\partial a}{\partial z}=\frac{\partial L}{\partial a}*a(1-a)=a-ydz=∂z∂L=∂a∂L∗∂z∂a=∂a∂L∗a(1−a)=a−y
z=w1∗x1+w2∗x2+......+bz=w1*x1+w2*x2+......+bz=w1∗x1+w2∗x2+......+b
dw1=∂L∂a∗∂a∂z∗∂z∂w1=dz∗x1dw1=\frac{\partial L}{\partial a}*\frac{\partial a}{\partial z}*\frac{\partial z}{\partial w1}=dz*x1dw1=∂a∂L∗∂z∂a∗∂w1∂z=dz∗x1
dw2=dz∗x2dw2=dz*x2dw2=dz∗x2
更新参数
w1:=w1−α⋅dw1w1:=w1-α·dw1w1:=w1−α⋅dw1
w2:=w2−α⋅dw2........w2:=w2-α·dw2........w2:=w2−α⋅dw2........
b:=w1−α⋅dbb:=w1-α·dbb:=w1−α⋅db