可穿戴传感器底层原理

摘要：传感器原理按过程基本分四层：现实层，电信号转换层，集成电路层，信号处理层。现实层将现实信息转换为传感器将要测量的量；电信号转换层是将测量量转换为电学信号；集成电路层通过电路设计使得电信号能够快速稳定准确的输出给开发人员；信号处理层通过运用高效的算法处理信号来实现各种应用。开发者的工作在于信号处理层，但是本篇主要内容在于现实层和电信号转换层。

加速度传感器

理论力学原理

• 测量质量块的惯性力，通过牛顿第二定律转化为加速度

什么是惯性力？

  物体做加速运动时，以物体本身为参考系，物体内部如同受到一个反方向的“力”一般，此力即惯性力。

• 简单例子
  
  当公交车加速时，站不稳的你会向后倾倒，不用抱怨谁在后面拉你，请把锅甩给惯性力。
  
• 惯性力是力？
  
  加速度运动的参考系，是非惯性系，非惯性系里牛顿定律是不适用的，然而为了能用牛顿定律去分析这个效果，故引入了惯性力这一概念。

惯性力与现实加速度的关系？

• 用坐标转换可得到三种加速度（物体在惯性系中的加速度$a_S$，物体在非惯性系中的加速度$a_{S^{{}^{\prime }}}$，非惯性系在惯性系中的加速度$a$）之间的关系

  $a_S=a_{S^{{}^{\prime }}}+a$

  我们需要测量的是非惯性系相对惯性系的加速度$a$，可以理解为你的智能手表在现实观测到的加速度。 用牛顿第二定律对非惯性系里的物体受力分析，有

  $F+f=m{a}_{S^{{}^{\prime }}}$

  其中$f$就是惯性力，F为表征出来就是真实力，移项转化得

  $f=m{a}_{S^{{}^{\prime }}}-F=-ma$*

  传感器直接测量的是应变，反映的是真实力F，而不是惯性力f，一般传感器内部相对运动很微弱，故$a_{S^{{}^{\prime }}}<<a$，故以现阶段的研究尺度有，$f=F=ma$

  实际上，$a_{S^{{}^{\prime }}}$的存在对加速度计的带宽，频率特性，灵敏度有很大影响。

电学原理

电学这一层面主要是测量物体内部因为惯性力产生的各种形变的，这里花样就多了

百度找到了7种：压电，压阻，电容，伺服，热电偶，谐振式，光波导

维基找到了27种：略。

可用于移动设备主要用压电式、压阻式、可变电容式

压电式(PE)

• 正压电效应
  压电材料在一定方向上受到外力而变形时，它的两个相对表面上会产生电位差，即电压。

  根据作用力对移动电荷的方向，可以识别出三种不同类型的效果，如图
  
  (A) 纵向, 输出电荷只与力成比例，与元件尺寸无关，机械串联和电路并联多个元件可增加电荷输出
  $Q_x=d_{xx}{F}_{x}n$
  其中，n为机械串联和电路并联的元件个数，d为该方向上的压电系数（下同）

  (B) 横向，电荷与材料几何尺寸相关，可微调元件提高敏感度
  $Q_x=d_{xy}{F}_{y}b/a$
  其中，a为元件横向上的尺寸，b为元件在电荷移动方向上的尺寸，

  (C) 剪切 ，输出电荷与元件的尺寸无关
  $Q_x=2d_{xx}{F}_{x}n$

• 压电材料
  用于加速度计的压电材料分为两类：单晶（通常为石英）和陶瓷材料。两者相比单晶寿命长，陶瓷灵敏度高。

• 基本结构

  • 剪切式
    压电材料夹在质量块和基底上的中心柱间，质量块与压电材料接触面几乎垂直于基底，竖直方向上的惯性力造成压电材料剪切式压电效应。这种设计大大减小了温度和基底应变带来的影响。

    

  • 压迫式
    压电材料夹在质量块和基底间，质量块被弹簧压在压电材料上，压力垂直于接触面。容易因为里面的基底热膨胀而产生测量误差。
    

  • 悬臂式
    杠杆一端固定住，质量块在杠杆另一端牵动着杠杆上的压电材料。因为杠杆放大了惯性力，灵敏度是最高的，但是因为这种头重脚轻的结构并不稳固，其谐振频率和带宽都很低。

• 压电集成电路：IEPE
  由上面介绍，我们知道压电式传感器并不需要外电源，但是这样产生的电流非常微弱，噪声也大，需要通过集成电路调节后输出。故产生了IEPE（Integral Electronic Piezoelectric），这是一类自带电量放大器或电压放大器的加速度传感器。

• 压电式加速度计常用于振动和冲击的测量

压阻式(PR)

• 压阻效应
  半导体受应力时，其电阻率发生变化

  实际的测量中，我们用欧姆定律测出电阻来计算出电阻率，电阻率公式为

  $R=\frac{\rho L}{S}$

  压阻元件通常为单晶硅，由于应变对单晶硅产生的压阻效应带来的电阻率$\rho$的变化远远大于对其产生的形变，故可以认为上式的横截面积S和长度L不会变化，即在压阻效应下，电阻率与电阻值成正比。

  压阻效应有各向异性特征，沿不同的方向施加应力和沿不同方向通过电流，其电阻率变化会不相同。用数学公式表达为：

  $\Delta R/R_0=\pi \sigma$

  其中，$\pi$为压阻系数张量，$\sigma$为应力张量，表现为矩阵相乘的形式，代入材料参数后结果为

  $\Delta R/R_0={\pi }_L{\sigma }_{xx}+{\pi }_T({\sigma }_{yy}+{\sigma }_{zz})$

这就和压电效应一样，压阻效应类型也分三个模式纵向力(A)、横向力(B)、和剪切力(C)，如下图所示

一般传感器会设计得只受到其中一种力F，另外另种将会微乎其微，这时电阻两端电压有

$V_r=R_{0}I(1+\pi F)$

其中$R_0$为原电阻

MEMS压阻式加速度传感器的结构除去电路部分与压电式基本一致，但与压电式同类设备相比，其优势在于能够测量的加速度下限可以达到 0 Hz。这种对低频加速度进行测量的能力，表明这种设备可以实现静态加速度的精确测量。但其有温度效应严重、灵敏度低的缺点。

• 电路结构
  压阻效应的加速度计需要电源，$\Delta R$要转化为电信号得通过惠斯通电桥来实现。
  

可变电容式(VC)

电容传感器具有低功耗，小尺寸，高可靠性的优点

可变电容式加速度计具有低噪音,低横轴敏感性,和高动态范围的优点，是移动穿戴的主流。

下图为电容式加速度计的基本构造，质量块受弹簧固定，加速时移动电极在固定电极之间移动。

• 加速度与电容的关系
  加速度由弹力推出，弹力可由单电容推出：

  • 惯性力等于弹力，移动电极移动的距离与惯性力的关系由胡克定律推出

    $F=-k\Delta X$

    k为弹性系数，$\Delta X$为电极移动距离

  • 电容极间距变化会改变电容大小，关系由平行平板电容的决定式给出

    $C=\frac{\epsilon S}{d}$

    ε为极板间介质的介电常数，ε=ε_rε₀，ε₀=1/4πk，S为极板面积，d为极板间距

• 多个电容组合优点

  • 每个移动电极和两侧的固定电极形成一对差动电容
    
    如图，中间电极位移使上下电容发生变化。以向上运动为例，C₁,C₂电容为：

    $C_1=\frac{\epsilon S}{d_0-|\Delta X|}$, $C_2=\frac{\epsilon S}{d_0+|\Delta X|}$

    $d_0$为初始极板间距，$\Delta X$为移动电极位移，则差动电容输出为：

    $\Delta C=C_1-C_2=\frac{\epsilon S}{d_0-|\Delta X|}-\frac{\epsilon S}{d_0+|\Delta X|}=C_0\frac{2\frac{|\Delta X|}{d}}{1-{\left(\frac{\Delta X}{d}\right)}^2}$

    $C_0$为原电容，由于实际中$\Delta X$相对于d非常小，即

    $\frac{|\Delta X|}{d}<<1$

    所以最终的差动电容为：

    $\Delta C\approx 2C_0\frac{|\Delta X|}{d}$

    由输出公式看出，差动电容的输出的线性度和灵敏度比单电容要好

  • 多组电容并联

    上面公式告诉我们$\Delta X$相对于d越小，线性度越高，测量越准确。
    然而MEMS传感器尺寸微小，导致初始极板间距d₀也很小，电容变化微弱。
    为了达到合适的量程，故设置了多对电容并联在一起来放大输出，另一方面也相当于多次测量，提高准确率。

• 三轴情况：

  x轴和y轴是与单轴一样的结构，z轴方向上质量块与芯片的衬底形成电容，通过测量这个单个电容来确定加速度，在这个轴上由于只有一个电容，且不能进行差分运算，故此方向的性能差一点。

• 阻尼
  结合最开始的理论力学，惯性力公式被忽略掉的一项$a_{S^{{}^{\prime }}}$实际上与外加速度的变化快慢和内部运动阻力有关。
  而内部阻力由材料弹力和摩擦力提供，而摩檫力造成内部运动的阻尼，加速度计都有都有阻尼，有些是故意的，有些则不是。
  • 过阻尼的问题在于传感器失去了有用的带宽。以电容加速度计为例，由于过阻尼弹簧更难拉动，一部分低频振动产生的信号将小到没有。
  • 对于欠阻尼器件，当加速度传感器在峰值响应附近被激发时，更容易出现信号失真和断裂现象。
    同样以电容加速度计为例，由于弹簧更容易拉动，故在外界加速度剧烈改变时造成实际测量的滞后和波动。

热感式

热感式MEMS加速度计内部没有任何质量块，它的中央有一个加热体，周边是温度传感器，里面是密闭的气腔，工作时在加热体的作用下，气体在内部形成一个热气团，热气团的比重和周围的冷气是有差异的，通过惯性热气团的移动形成的热场变化让感应器感应到加速度值。

由于涉及流体力学复杂，现实层面的推导就不来了

陀螺仪

理论力学原理

让一个质量块做振荡式来回运动，当旋转时，会产生科里奥利力，此时就可以对其进行测量，从而得出旋转角速度。

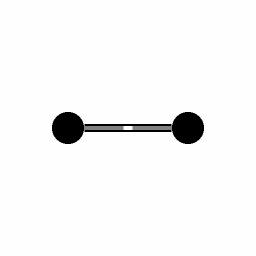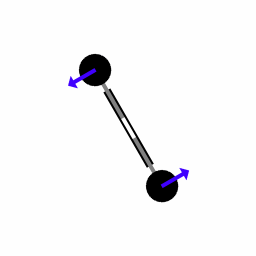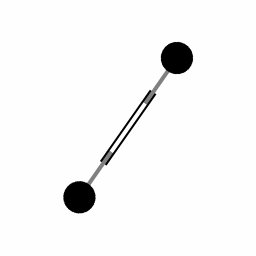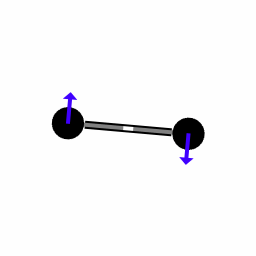
• 科里奥利力与角速度关系

科里奥利力是属于旋转参照系的惯性力。在以旋转的情况下，外部看到的直线运动会在旋转体系中变成曲线运动，就如同物体受到力的作用一般。

科里奥利力公式为

$F=-2m{v}^{{}^{\prime }}\times \omega$

式中F为科里奥利力；m为质点的质量；v’为相对于转动参考系质点的运动速度（矢量）；ω为旋转体系的角速度（矢量）；$\times$ 表示两个向量的外积符号（大小等于两模与两矢量夹角的正弦值的乘积，方向满足右手螺旋定则）

只考虑物体速度方向与旋转轴垂直的情况，等式两边消掉质量后为 a=2*ωv，其中a为科里奥利加速度，测量此加速度的方法和加速度计测量原理基本一致，而物体相对于旋转系的速度由简谐运动中质量块的振动长度和频率决定，故代入式中可以解出角速度ω。

补充科里奥利力公式推导：

电学原理

市面上的移动穿戴基本都是mems陀螺仪，此类陀螺仪主要以变电容的方式测量科里奥利加速度从而得出角速度
下面以ADI的MEMS陀螺仪为例，介绍其电学原理

图片来自B站ADI官方视频，显然这种陀螺仪两边就是电容式加速度计

在静止的情况下，图中的谐振器以一定的频率左右振动，此时左右区域的电容间距没有改变，测量出的角速度也为0

当加上旋转后，由于科里奥利力的作用，谐振器会在腔体中扭起来，产生竖直方向的位移，使两边电容产生变化，从而可推出科里奥利加速度（电容加速度计原理），从而推出加速度（科里奥利力公式）

• 双核改进
  
  这里有一个问题，实际上使用中的陀螺仪并不会老老实实地静止，经常会在垂直于电容极板的方向上产生振动，这时再去测量角速度会造成很大的误差。

  因此，ADI 公司设计了双核的陀螺仪，如图其构造是由两个质量相同，振动相位差180度的质量块构成。当正常旋转时，两个质量块受到相反的科里奥利力，对于电容的变化也相反，反馈到电信号上是一对差分信号（振幅相同，相位相反），故将两个信号接入差分运算放大器中得出最终的测量值，提高了线性稳定性和准确度。

  

  当受到振动时，两个质量块将会同上同下运动，电容变化产生的信号是一对共模信号，则经过差分电路做差后刚好可以抵消掉此信号。

  

  所以，当你使用陀螺仪辅助瞄准功能来打FPS射击游戏时，如果瞄不准敌人，并不一定是你的技术不行，更有可能是手机里的陀螺仪不行，不能防抖。

光学心率传感器

基本原理

光电容积脉搏波描记法是此类传感器的基本原理:当光照透过皮肤组织然后再反射或透射到光敏传感器时光照有一定的衰减的。像皮脂、纤维、静脉和其他连接组织等等对光的吸收是基本不变的，由于动脉里血液容积随心脏的收缩与舒张产生周期性变动，那么对光的吸收自然也有所变化，故通过检测光反射量即可确定心率波动。

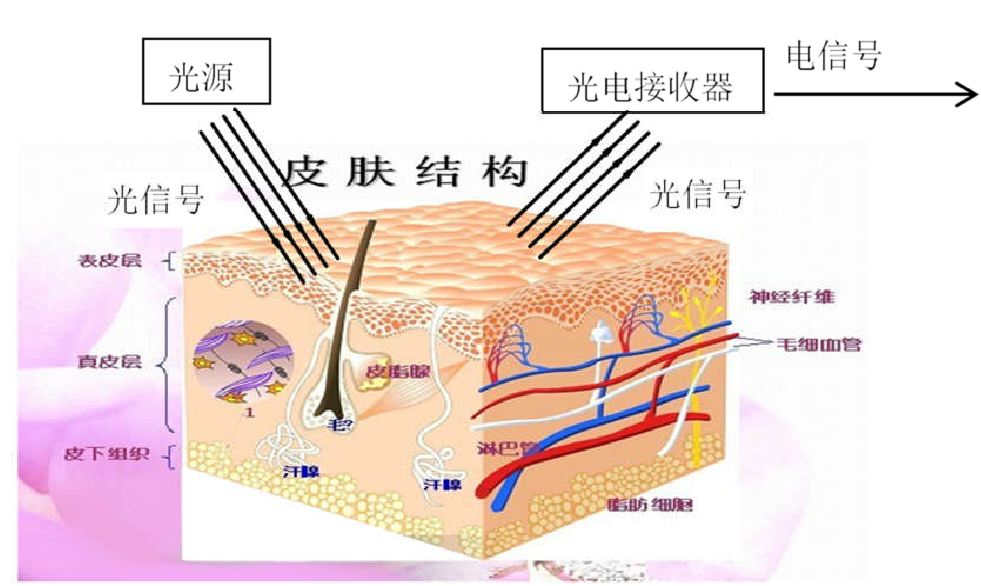
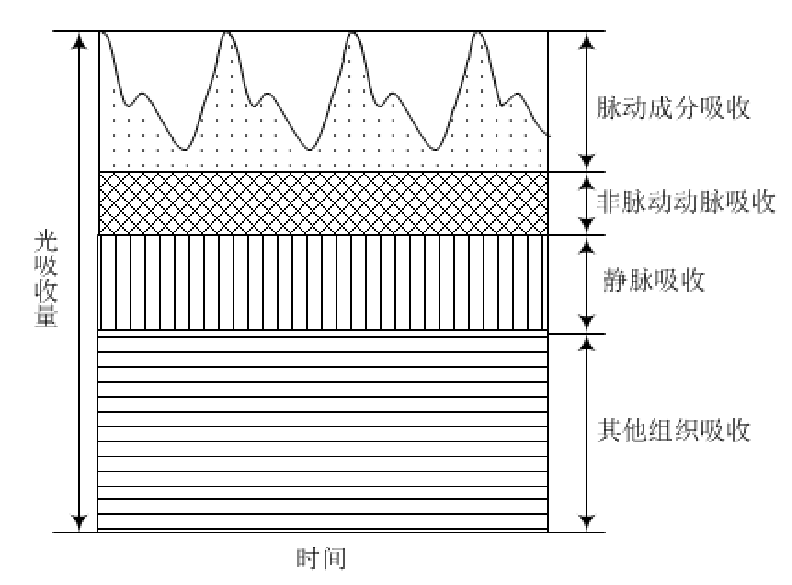
朗伯-比尔定律

朗伯比尔定律描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系，公式的对数形式为

$A=lg(I_0/I)=lg(1/T)=Kbc$

指数形式为：

$I=I_0{e}^{-Kbc}$

• A 为吸光度，T 为透射比(透光度)，是出射光强度 $I$ 与入射光强度 $I_0$ 的比值

• K 为摩尔吸光系数，它与吸收物质的性质及入射光的波长λ有关

• c 为吸光物质的浓度，单位为 mol/L，b 为吸收层厚度，单位为cm

心脏收缩，血管里的血液容积变多，光经过的血液的厚度b增加，故总吸光度增加，反射光量减少，心脏收缩时相反。

入射光波长选择

波长的选择原则：
被测物质对检测光吸收程度较高，其他物质对检测光的吸收程度较低的特定波长，由此测得脉搏波信号的信噪比较高。

• 绿光效果明显

  下图是手指反射比和血液透射比光谱图，可以看出小于 500 nm的波长的光已经被吸收殆尽了，基本没有反射光可测；大于 500 nm波长的光中，578 nm是血液相对于其他组织最容易吸收的光波长。

• 红光/红外穿透强

  绿光虽然吸收明显，但容易被水分吸收，测不到真皮层的血液信息，这时就需要波长长一点的光。

  血红蛋白中的含氧量可以决定光吸收量。其中
  的血红蛋白主要有氧合(Hb O2)和脱氧(Hb)两种存在形式，在波长为 600~1000 nm
  的连续光谱中，Hb O2 和 Hb 的光吸收系数如图所示
  

考虑到这一步，为了减少因为呼吸带来血氧浓度变化的影响，一般选取两者吸收率相近的波长为840 nm左右。

血氧饱和度传感器

生物光子学原理

血氧饱和度 (SpO2) 定义

即血液中氧合血红蛋白HbO2的容量占全部可结合的血红蛋白容量的百分比，Hb为未于氧结合的还原血红蛋白。

血氧饱和度的测量原理也是基于光电容积脉搏波描记法。通过朗博比尔定律分别”测出“氧合血红蛋白和还原血红蛋白的浓度变化，从而得到血氧饱和度。

检测光选择大于600 nm的光，因为只有大于600 nm才会到达真皮层，那里有丰富的血管，交流分量大。再根据两者蛋白对不同波长光的吸收比差异，一般选择红光660 nm左右测还原蛋白和940 nm左右检测氧化蛋白，其中660 nm是因为两者差距很大可以使最后线性公式的截距和斜率减小，输出更加稳定，940 nm则是在这种情况下两者相距小便与推导过程中公式化简

透射型血氧检测数学推导

当光强为$I_{in}$的单色光入射到人体组织中，由朗伯比尔定律，有

$I_{out}=I_{in}\ast e^{-{\epsilon }_0{C}_0{L}_0}\ast e^{-{\epsilon }_{Hb{O}_2}{C}_{Hb{O}_2}L}\ast e^{-{\epsilon }_{Hb}{C}_{Hb}L}$

其中，L均为各自的光路径长度，${\epsilon }_{}$、$C_{}$分别为静态组织、氧化蛋白，还原蛋白（从左到右）的吸光系数和吸光物质浓度。

因为心脏搏动会引起血管充血，此时光径长度由$L$变为$L+\Delta L$，透射光强从$I_{DC}$变为$I_{DC}-I_{AC}$，此时在增加的血液容积部分$\Delta L$中有

$I_{DC}-I_{AC}=I_{DC}\ast e^{-({\epsilon }_{Hb{O}_2}{C}_{Hb{O}_2}+{\epsilon }_{Hb}{C}_{Hb})\Delta L}$

变形，得

$ln[1+\frac{-I_{AC}}{I_{DC}}]=-({\epsilon }_{Hb{O}_2}{C}_{Hb{O}_2}+{\epsilon }_{Hb}{C}_{Hb})\Delta L$

由于透射光减少的光强$I_{AC}$占整个透射光强的比例很小，即$\frac{I_{AC}}{I_{DC}}\to 0$，所以由等价无穷小关系

${\lim }_{x\to 0}\frac{ln(1+x)}{x}=1$

可得出 $ln[1+\frac{-I_{AC}}{I_{DC}}]=\frac{-I_{AC}}{I_{DC}}$

最后代回原方程，有

$\frac{I_{AC}}{I_{DC}}=({\epsilon }_{Hb{O}_2}{C}_{Hb{O}_2}+{\epsilon }_{Hb}{C}_{Hb})\Delta L$

设两束光波长分别为${\lambda }_1$和${\lambda }_2$，令
$D_{{\lambda }_1}=\frac{I_{AC}^{{\lambda }_1}}{I_{DC}^{{\lambda }_1}}$， $D_{{\lambda }_2}=\frac{I_{AC}^{{\lambda }_2}}{I_{DC}^{{\lambda }_2}}$

则有$\frac{D_{{\lambda }_1}}{D_{{\lambda }_2}}=\frac{I_{AC}^{{\lambda }_1}/I_{DC}^{{\lambda }_1}}{I_{AC}^{{\lambda }_2}/I_{DC}^{{\lambda }_2}}=\frac{{\epsilon }_{Hb{O}_2}^{{\lambda }_1}{C}_{Hb{O}_2}^{{\lambda }_1}+{\epsilon }_{Hb}^{{\lambda }_1}{C}_{Hb}^{{\lambda }_1}}{{\epsilon }_{Hb{O}_2}^{{\lambda }_2}{C}_{Hb{O}_2}^{{\lambda }_2}+{\epsilon }_{Hb}^{{\lambda }_2}{C}_{Hb}^{{\lambda }_2}}$

因为两种光测量的是同一浓度下的血红蛋白，故有$C_{Hb{O}_2}^{{\lambda }_1}=C_{Hb{O}_2}^{{\lambda }_2}$，$C_{Hb{O}_2}^{{\lambda }_1}=C_{Hb{O}_2}^{{\lambda }_2}$，再把上式代入SpO₂定义式中，有

$Sp{O}_2=\frac{{\epsilon }_{Hb}^{{\lambda }_2}(D_{{\lambda }_1}/D_{{\lambda }_2})-{\epsilon }_{Hb}^{{\lambda }_1}}{({\epsilon }_{Hb{O}_2}^{{\lambda }_1}-{\epsilon }_{Hb}^{{\lambda }_1})-({\epsilon }_{Hb{O}_2}^{{\lambda }_2}-{\epsilon }_{Hb}^{{\lambda }_2})(D_{{\lambda }_1}/D_{{\lambda }_2})}$

这时选取的特定波长${\lambda }_2$，尽可能使得${\epsilon }_{Hb}^{{\lambda }_2}={\epsilon }_{Hb{O}_2}^{{\lambda }_2}$，再代入上式，得

$Sp{O}_2=\frac{{\epsilon }_{Hb}^{{\lambda }_1}}{{\epsilon }_{Hb}^{{\lambda }_1}-{\epsilon }_{Hb{O}_2}^{{\lambda }_1}}-\frac{{\epsilon }_{Hb}^{{\lambda }_2}}{{\epsilon }_{Hb}^{{\lambda }_1}-{\epsilon }_{Hb{O}_2}^{{\lambda }_1}}\frac{D_{{\lambda }_1}}{D_{{\lambda }_2}}$

至此，由于各种吸收系数$\epsilon$可看作常数，所以血氧浓度与$\frac{D_{{\lambda }_1}}{D_{{\lambda }_2}}=\frac{I_{AC}^{{\lambda }_1}/I_{DC}^{{\lambda }_1}}{I_{AC}^{{\lambda }_2}/I_{DC}^{{\lambda }_2}}$呈线性关系。

故最终式可写为

$Sp{O}_2=A+B\frac{I_{AC}^{{\lambda }_1}/I_{DC}^{{\lambda }_1}}{I_{AC}^{{\lambda }_2}/I_{DC}^{{\lambda }_2}}$

其中系数项是吸收系数的分式，很难测量不同人组织中的光吸收系数，所以一般会套用用经验公式，经验公式可通过实验数据线性回归得到。

由下图所示，上式中直流分量$I_{DC}=I_{min}$，交流分量$I_{AC}=I_{max}-I_{min}$

反射型血氧传感器与透射型的关系

现在市场上的穿戴设备基本都是反射型的，但是测量公式形式上和透射型的一样。说是反射型，其实上对交流分量起决定作用的是血红蛋白的散射光变化。

光在介质中的散射作用一般可分为三种：

• 瑞利散射：光波长远大于粒子直径时才有，与入射光波长保持一致
• 米氏散射：光波长与粒子直径相当时才有
• 拉曼散射：一直有，但是一般小于其他两个散射两个数量级，会改变散射光波长
  

血红蛋白的直径约为 5 nm，入射光的波长大于 600 nm，显然血红蛋白主要散射是瑞利散射。根据瑞利散射定律，有

$I=I_0\frac{8{\pi }^4{\alpha }^2}{{\lambda }^4{R}^2}(1+co{s}^2\theta )$

其中，$\alpha$为分子的极化率，R为粒子半径，$\theta$是入射光角度与散射光的夹角；在静态下以上几个参数视为定值，此时可视为散射光强度与入射光强度之间成正比，再结合最开始的朗伯比尔定律可推出：在静态介质和固定观测角度情况下，散射光和透射输出光成正比，故最后的公式一样都为：

$Sp{O}_2=A+B\frac{I_{AC}^{{\lambda }_1}/I_{DC}^{{\lambda }_1}}{I_{AC}^{{\lambda }_2}/I_{DC}^{{\lambda }_2}}$

补充：修正的朗伯比尔定律

由于此场景需要比较高的准确度，考虑到皮肤组织的散射作用，改用修正的朗伯比尔定律来描述被测物质的浓度

• OD为光密度，光吸收度的另外一种表示；
• α是比消光系数，描述不同波长光在物质中的衰减程度，与透射物质和波长有关；
• C为吸光物质的浓度；B为散射因子，用来描述散射引起的光程增加，与物质种类和波长有关；
• l为光的传播路径；G代表背景消耗。

此定律更为准确，但是实际条件下难以计算。由此定律，可以在经验公式加入非线性的分量来增加准确度，令$R=\frac{D_{{\lambda }_1}}{D_{{\lambda }_2}}=\frac{I_{AC}^{{\lambda }_1}/I_{AC}^{{\lambda }_1}}{I_{DC}^{{\lambda }_2}/I_{DC}^{{\lambda }_2}}$，则改进的公式为：

$Sq{O}_2=A+B{R}^2+C{R}^2$

电极式心率传感器（ECG sensor）

心脏的电生理学原理

首先，让我们感受一下心脏的内部运动，看看下面的动图，摸一摸自己的心脏，感觉一下它的力量。

在每一次心脏跳动中，你应该只能感觉到一次最大的起伏，但是实际上总共有三种在时间上错开的起伏，这是由心脏三块不同的肌肉所引起的，医学上对于这三块肌肉是有针对性分别测量的。我们感受不到的是下图的P峰和T峰，这两个峰对与心脏病的检测有巨大的影响，如果你的传感器连这都测不到，那就别谈什么医学检测了。

• ECG传感器的实质
  

1. 心脏跳动产生心电，相当于电池。

2. 人体是导体，且其他部位的生物电弱很多，故相当于导线，但距心脏越远损耗越大

3. 传感器则是一个灵敏电流表

4. ECG就是整个回路的电流随时间变化的信号。

   所以大体上可以总结出，ECG效果好不好，关键看三点：心脏好不好，
   测量部位远不远，电流表零不灵敏、抗噪效果如何

当ECG碰上PPG

ECG的峰值直接源于心室，而PPG的峰值则是因为血管收缩所造成的。因此我们可以得到血液自心脏送出后到达量测部位的传输时间，也就是脉搏波传递时间Pulse Transit Time (PTT)，脉搏波传递的速度与血压是直接相关的，血压高时，脉搏波传递快，反之则慢。

所以，我们可以通过心电信号ECG与脉搏波信号PPG获得脉搏传递时间PTT，再加上常规的一些身体参数 (如身高、体重) 即可得出脉搏波传递速度，通过建立的特征方程来估计人体脉搏的收缩压与舒张压，可实现无创连续血压测量。

磁力计

基于霍尔效应原理

在半导体薄膜两端通以控制电流 I，并在薄膜的垂直方向施加磁感应强度为B的匀强磁场，半导体中的电子与空穴受到不同方向的洛伦兹力而在不同方向上聚集，在聚集起来的电子与空穴之间会产生电场，电场强度与洛伦兹力产生平衡之后，不再聚集，这个现象叫做霍尔效应。在垂直于电流和磁场的方向上，将产生的内建电势差，称为霍尔电压U。

霍尔电压U与半导体薄膜厚度d，电场B和电流I的关系为U=k(IB/d)。这里k为霍尔系数，与半导体磁性材料有关。

基于各向异性磁阻效应（AMR）

磁阻效应

引入电动力学的洛伦兹公式：
$$F=qv\times B+qE$$

磁阻效应产生的原因与霍尔效应一样，都为磁体中洛伦兹力对内部电荷的作用。由于洛伦兹力与速度相关，在洛伦兹力与电场力平衡形成后，有一个速度使载流子正常通过磁体，快于这个速度的载流子则偏向洛伦兹力，慢于这个速度的载流子则偏向电场力。这种偏转会使得原先通过磁体的载流子减少，引起电阻的增加。

各向异性磁电阻效应

• 当外部磁场与磁体电场方向成零度角时, 电阻是不会随着外加磁场变化而发生改变的
• 当外部磁场与磁体电场有一定角度的时候, 磁体内部磁化矢量会偏移，薄膜电阻降低。阻值变化与磁化强度矢量和电流矢量之间夹角的正弦平方成正比

既然最后要测量微小的电阻变化，那么就必须得用惠斯通电桥，AMR磁传感器的基本结构由四个磁阻组成了惠斯通电桥

• 偏置磁场的作用是为了在无外加磁场时测出的输出电压不为0，保证测量过程中电压不会反向

• 在惠斯通电桥组成的平面内，每个磁场角度对应得输出电压不同
  通过测试电桥的两输出端输出差电压信号，可以得到外界磁场值。
  

光学传感器

基于内光电效应：由光引起的电学材料固有性质的改变，器件为光敏二极管，光电阻

基于外光电效应：由光引起的电学材料中的电子溢出，器件为光电二极管

光电二极管和光敏二极管殊途同归，典型电路包括一个光电二极管、一个电流放大器和一个低通滤波器，以检测并处理光输入引起的输出电压信号。

二极管反向偏置，基本没有电流通过，当光照时通过电流增加，Rf阻值增加，从而产生电位变化。

至于光电阻，其电路可以很简单

气压传感器

高精度气压传感器一般是利用MEMS技术在单晶硅片上加工出真空腔体和惠斯登电桥，惠斯登电桥桥臂两端的输出电压与施加的压力成正比，经过温度补偿和校准后具有体积小，精度高，响应速度快，不受温度变化影响的特点。

又双叒叕是惠斯通电桥，此电桥专测微小的电阻变化，这里就不详细说明了。

总结

   发明传感器的人没一个是搞计算机的，但是传感器为计算机提供了外界信息的接口，这才使得移动计算得以实现。正如“不懂硬件的软件开发者不是一个好开发者“一样，学习点底层的知识也是有好处的。