LC-1483. 树节点的第 K 个祖先（树上倍增算法）

1483. 树节点的第 K 个祖先

难度困难134

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

实现 TreeAncestor 类：

TreeAncestor（int n， int[] parent） 对树和父数组中的节点数初始化对象。
getKthAncestor``(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

示例 1：

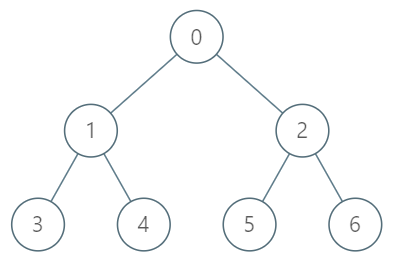
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]输出：
[null,1,0,-1]解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

提示：

1 <= k <= n <= 5 * 104
parent[0] == -1 表示编号为 0 的节点是根节点。
对于所有的 0 < i < n ，0 <= parent[i] < n 总成立
0 <= node < n
至多查询 5 * 104 次

树上倍增算法

https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/solution/mo-ban-jiang-jie-shu-shang-bei-zeng-suan-v3rw/

预处理出每个节点的第 2^i个祖先节点，即第 2,4,8.... 个祖先节点(注意 x 的第1 个祖先节点就是 parent[x]。由于任意 k 可以分解为若干不同的 2 的幂(例如 13 = 8+4+1)，所以只需要预处理出这些 2^i 祖先节点，就可以快速地到达任意第 k 个祖先节点

例如 k = 13 = 8+4+1 = 1101_(2)，可以先往上跳 8 步，再往上跳 4步和1步;也可以先往上跳1步，再往上跳 4 步和 8 步。无论如何跳，都只需要跳 3 次就能到达第 13 个祖先节点据此，可以得到下面的算法。

算法：

在构造函数 TreeAncestor 中，预处理出每个节点 x 的第 2^i 个祖先节点，记作 pa[x][i] (若第 2^i 个祖先节点不存在则 pa[x][i] = -1) 。计算方式如下

先枚举 i，再枚举 x。相当于先算出所有爷爷节点，再算出所有爷爷的爷爷节点，依此类推.

pa[x][0]=parent[x]，即父节点。

pa[x][1]=pa[pa[x][0]][0]，即爷爷节点。

一般地，pa[x][i+1]=pa[pa[x][i]][i]。如果 pa[x][i] = -1 则 pa[x][1+1] = -1

这里 i+1至多为 logn 。例如 n = 13 时，log13 = 3，至多需要预处理到第 2^3 个祖先节点。 (当然，你也可以先把树高，或者每个节点的深度求出来，再据此做精细地计算。)

class TreeAncestor {private int[][] pa;public TreeAncestor(int n, int[] parent) {int m = 32 - Integer.numberOfLeadingZeros(n); // n 的二进制长度// 预处理出每个节点 x 的第 2^i 个祖先节点，记作 pa[x][i] pa = new int[n][m];for(int i = 0; i < n; i++){pa[i][0] = parent[i];}// 先枚举 `i`，再枚举 `x`。相当于先算出所有爷爷节点，再算出所有爷爷的爷爷节点，依此类推for(int i = 0; i < m-1; i++){for(int x = 0; x < n; x++){int p = pa[x][i];pa[x][i+1] = p < 0 ? -1 : pa[p][i];}}}public int getKthAncestor(int node, int k) {int m = 32 - Integer.numberOfLeadingZeros(k); // k 的二进制长度for(int i = 0; i < m; i++){if(((k >> i) & 1) > 0){ // k 的二进制从低到高第 i 位是 1node = pa[node][i];if(node < 0) break; // 如果node=-1, 说明第k个祖先节点不存在}}return node;}
}