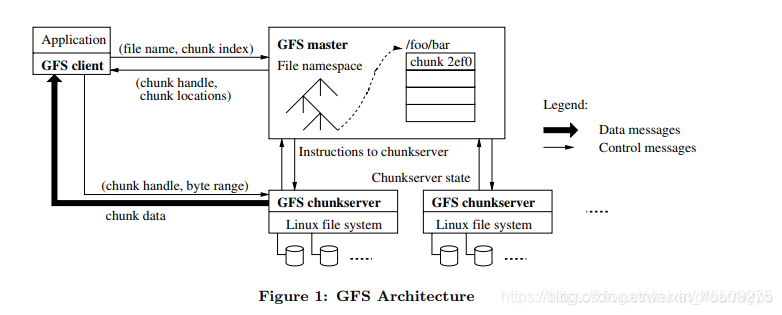
GF
(gf.pas)
【背景】
找啊找啊找GF,找到一个好GF,吃顿饭啊拉拉手,你是我的好GF.再见."
"诶,别再见啊..."
七夕...七夕...七夕这个日子,对于sqybi这种单身的菜鸟来说是多么的痛苦...虽然他听着这首叫做"找啊找啊找GF"的歌,他还是很痛苦.为了避免这种痛苦,sqybi决定要给自己找点事情干.他去找到了七夕模拟赛的负责人zmc MM,让她给自己一个出题的任务.经过几天的死缠烂打,zmc MM终于同意了.
但是,拿到这个任务的sqybi发现,原来出题比单身更让人感到无聊-_-....所以,他决定了,要在出题的同时去办另一件能够使自己不无聊的事情--给自己找GF.
sqybi现在看中了n个MM,我们不妨把她们编号1到n.请MM吃饭是要花钱的,我们假设请i号MM吃饭要花rmb[i]块大洋.而希望骗MM当自己GF是要费人品的,我们假设请第i号MM吃饭试图让她当自己GF的行为(不妨称作泡该MM)要耗费rp[i]的人品.而对于每一个MM来说,sqybi都有一个对应的搞定她的时间,对于第i个MM来说叫做time[i]. sqybi保证自己有足够的魅力用time[i]的时间搞定第i个MM^_^.
sqybi希望搞到尽量多的MM当自己的GF,这点是毋庸置疑的.但他不希望为此花费太多的时间(毕竟七夕赛的题目还没出),所以他希望在保证搞到MM数量最多的情况下花费的总时间最少.
【问题描述】
sqybi现在有m块大洋,他也通过一段时间的努力攒到了r的人品(这次为模拟赛出题也攒rp哦~~).他凭借这些大洋和人品可以泡到一些MM.他想知道,自己泡到最多的MM花费的最少时间是多少.
注意sqybi在一个时刻只能去泡一个MM--如果同时泡两个或以上的MM的话,她们会打起来的...
【数据输入】
输入的第一行是n,表示sqybi看中的MM数量.
接下来有n行,依次表示编号为1, 2, 3, ..., n的一个MM的信息.每行表示一个MM的信息,有三个整数:rmb, rp和time.
最后一行有两个整数,分别为m和r.
【数据输出】
你只需要输出一行,其中有一个整数,表示sqybi在保证MM数量的情况下花费的最少总时间是多少.
【样例输入】
4
1 2 5
2 1 6
2 2 2
2 2 3
5 5
【样例输出】
13
【时间限制】
每个测试点1s
【注释】
sqybi说:如果题目里说的都是真的就好了...
sqybi还说,如果他没有能力泡到任何一个MM,那么他就不消耗时间了(也就是消耗的时间为0),他要用这些时间出七夕比赛的题来攒rp...
原题数据范围:
对于20%数据,1<=n<=10;
对于100%数据,1<=rmb<=100,1<=rp<=100,1<=time<=1000;
对于100%数据,1<=m<=100,1<=r<=100,1<=n<=100.
这道题和之前的01背包不同的地方是有两个容量,所以要开二维数组,其次这道题的题目要求导致这里面有两个关键字,而且人数和时间是从属关系,因此在人数变化了之后,时间就会跟着变化,所以这里面就要手动操作max函数的选择,而且要注意这里面的是否更新的两种情况不可以合并。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<sstream>
#include<fstream>
using namespace std;int v1[110],v2[110];
int w[110];
int f[110][110];
int g[110][110];int main()
{//for(int ii=1;ii<=10;ii++){//stringstream ss;//ss<<ii;//string sss ="gf"+ss.str()+".in";//printf("%s\n",sss.c_str());//freopen(sss.c_str(),"r",stdin);freopen("gf6.in","r",stdin);int n,m,t,i,j,k;scanf("%d",&n);//printf("%d\n",n);for( i=1;i<=n;i++){scanf("%d%d",&v1[i],&v2[i]);scanf("%d",&w[i]);}scanf("%d%d",&m,&t);f[0][0] = 0;int maxg = 0;for( i=1;i<=n;i++)for( j=m;j>=v1[i];j--){for( k=t;k>=v2[i];k--){if ((g[j-v1[i]][k-v2[i]]+1 > g[j][k]) ||(g[j-v1[i]][k-v2[i]]+1 == g[j][k] && f[j-v1[i]][k-v2[i]]+w[i] < f[j][k])){g[j][k] = g[j-v1[i]][k-v2[i]]+1;f[j][k] = f[j-v1[i]][k-v2[i]]+w[i];maxg = max(maxg, g[j][k]);}}///for(k=v2[i]-1;k>=0;k--)///{///g[j][k]=g[][];}int ans = (1<<30)-1;for (int i=1; i<=m; i++)for (int j=1; j<=t; j++)if (g[i][j] == maxg) ans = min(ans,f[i][j]);printf("%d\n",ans);fclose(stdin);}return 0;
}