哈夫曼树和哈夫曼编码

news/2024/11/28 1:34:06/

一.哈夫曼树

1.哈夫曼树

哈夫曼树是一种用于编码的树形结构。它是通过将频率最低的字符反复组合形成的二叉树，使得出现频率高的字符具有较短的二进制编码，而出现频率低的字符具有较长的编码。

在哈夫曼树中，每个叶子节点都代表一个字符，其权值表示该字符在文本中出现的次数。非叶子节点代表的权值为其两个子节点的权值之和。因此，从根节点到叶子节点的路径上的数字串即为该字符的哈夫曼编码。

在编码时，对于要编码的文本，把其中的每个字符用哈夫曼树的编码替换掉即可。解码时，从哈夫曼树的根节点开始，按照编码的数字串依次向下走，直到到达叶子节点，即可得到原来的字符。

哈夫曼树的应用广泛，常用于数据压缩、加密等领域。

2.构造哈夫曼树原理

给定n个权值分别为w1，w2… wn。的结点，构造哈夫曼树的算法描述如下:

  • 1)将这n个结点分别作为n棵仅含一个结点的二又树，构成森林F.
  • 2)构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和。
  • 3)从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
    4)重复步骤2)和3)，直至F中只剩下一棵树为止。

从上述构造过程中可以看出哈夫曼树具有如下特点:

  • 1)每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大。
  • 2)构造过程中共新建了n-1个结点(双分支结点)，因此哈夫曼树的结点总数为2n- 1
  • 3)每次构造都选择2棵树作为新结点的孩子，因此哈夫曼树中不存在度为1的结点。

二.哈夫曼编码

哈夫曼编码的原理是通过构建哈夫曼树来实现的。具体地，首先统计给定文本中每个字符出现的频率，并将它们作为叶子节点构建出一棵二叉树。接着，反复合并权值最小的两个节点，得到新节点，将它们加入哈夫曼树中，直至所有节点都被合并成为一个根节点。在此过程中，左分支标记为0，右分支标记为1。最终得到的哈夫曼树即为字符的哈夫曼编码。

举例来说，对于输入字符串"ABBCCCDDDDEEEEE"，它包含了5种不同的字符 A、B、C、D 和 E，它们分别出现的次数为 1, 2, 3, 4 和 5。我们可以按照上述步骤构建出一个哈夫曼树，如下所示：

          +--------+|   15   |+--------+|+--------+--------+|         |        |+---+      +---+    +---+| B |      | C |    | D |+---+      +---+    +---+/ \        / \      / \1/   \2    1/   \2  1/   \3+----+ +---+ +--+  +---+  +--+| A  | | E | |   |  |   |  |  |+----+ +---+ +--+  +---+  +--+

在这个哈夫曼树中，每个叶子节点代表一个字符，其权值表示该字符在文本中出现的次数。非叶子节点代表的权值为其两个子节点的权值之和。从根节点到叶子节点的路径上的数字串即为该字符的哈夫曼编码。例如，E 的编码为 0，B 的编码为 10，C 的编码为 11，D 的编码为 2（注意这里是二进制编码），A 的编码为 30。

对于给定的文本，我们可以将其中的每个字符用哈夫曼树的编码替换掉，得到压缩后的二进制串。解压时，从哈夫曼树的根节点开始，按照编码的数字串依次向下走，直到到达叶子节点，即可得到原来的字符。

三.补充知识

1.C语言排序函数

qsort() 函数是 C 语言中的标准库函数，用于对数组进行排序。它的语法如下所示：

void qsort(void *base, size_t nmemb, size_t size, int (*compar)(const void*, const void*));

该函数接收四个参数，分别是：

  • void *base：需要排序的数组的首地址；
  • size_t nmemb：数组中元素的个数；
  • size_t size：每个数组元素占用的字节数；
  • int (*compar)(const void*, const void*)：指向比较函数的指针。

其中，比较函数必须返回一个整数值，表示两个元素之间的关系，具体规定如下：

  • 若返回值小于 0，则表示第一个元素应该排在第二个元素之前；
  • 若返回值等于 0，则表示两个元素相等，无需改变它们在数组中的位置；
  • 若返回值大于 0，则表示第一个元素应该排在第二个元素之后。

因为 qsort() 函数会直接操作原数组，因此在使用时需要保证比较函数和数据类型的匹配、越界访问等问题，以避免出现未定义行为。

2.占位符

在计算机科学中，占位符是一个表示数据的特殊字符或值。它通常用于代替实际数据或者标识出不存在的数据。

一些常见的占位符包括：

  1. 空格：在文本中，空格常被用作占位符。例如，在编程语言中，空格可以用于分隔单词或语句。
  2. 通配符：在搜索引擎、文件管理器和数据库查询等应用程序中，通配符（如 * 和 ?）可以用来匹配任意字符或字符串。它们可以帮助用户快速查找文件或记录。
  3. 十六进制码：在编程领域，十六进制码可以用作占位符表示某个未知的数值。它们也可以用于调试和修复代码中的错误。
  4. 填充字符：在格式化输出时，填充字符（如 0 或空格）可以用于在数字前面添加零或空格，以满足格式要求。
  5. 标记：在自然语言处理中，标记可以用于表示某个词汇或短语的类型。例如，POS（Part-of-Speech）标记可以用于表示一个单词是名词、动词还是形容词。
  Node* parent = newNode(nodes[0]->weight + nodes[1]->weight, '-');

在这行代码中，'-'是一个占位符，用于表示新节点不代表任何字符或叶子节点。当构造哈夫曼树时，每个非叶子节点都需要有两个子节点，因此在将两个权重最小的节点合并成一个新节点时，需要创建一个没有对应字符的节点，以便作为它们的父节点。在这种情况下，可以使用一个占位符来表示该节点不代表任何字符。

四.核心功能实现

1.构造哈夫曼树

//构造哈夫曼树
HTree *createHTree(int n,char values[],int weights[]){HTnode *nodes = (HTnode*)malloc(sizeof(HTnode)*n);          //建立一个结点数组for (int i = 0; i < n; ++i) {nodes[i] = creatennode(weights[i], values[i]);          //给每一个结点赋值}while (n > 1) {// 对节点按照权重从小到大排序qsort(nodes, n, sizeof(HTnode), cmp);             //C语言的排序函数// 取出两个权重最小的节点构造一个新的父节点HTnode parent = creatennode(nodes[0]->weight + nodes[1]->weight, '-');  //构造它们的和结点，修改左右指针parent->lchild = nodes[0];parent->rchild = nodes[1];// 将新节点插入到原来的节点集合中，并将原来的两个子节点从集合中删除nodes[0] = parent;             for (int i = 2; i < n; ++i) {            //其实这并不是严格的删除操作，相当于数组0号元素重载，然后从2号元素开始向前移动一个位置nodes[i - 1] = nodes[i];}n--;}HTnode root = nodes[0];              //当剩下最后一个结点时，就是我们的根结点free(nodes);return root;
}

2.哈夫曼编码

//根据哈夫曼树输出哈夫曼编码
void print_code(HTnode &node, int* code, int len) {// 如果是叶子节点，打印它的字符和对应编码if (node->lchild == NULL && node->rchild == NULL) {printf("%c的哈夫曼编码: ", node->val);for(int i=0;i<len;i++){printf("%d ",code[i]);}printf("\n");}else {// 递归左子树，在编码末尾加上0code[len] = 0;print_code(node->lchild, code, len+1);// 递归右子树，在编码末尾加上1code[len] = 1;print_code(node->rchild, code, len+1);}
}

3.遍历哈夫曼树

这里应该算全文最简单的了，因为上一篇博客我已经写了二叉树的相关操作，；里面有二叉树的遍历，欢迎点击同专栏的二叉树的相关操作查看。

void visit1(HTnode &T){printf("%d\t",T->weight);             //这里遍历本来应该是输出value的，但是在构造二叉树的时候我们创建了新结点，其值是占位符，所以这里选择打印权值
}//这里我们采用先序遍历
void Preorder(HTnode &T){if(T!=NULL){visit1(T);        //在访问函数里面定义我们想要的可视化输出Preorder(T->lchild);Preorder(T->rchild);}
}

五.完整代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <windows.h>#define N 50         //叶子结点总数 
#define M 2*N-1      //树中结点总数//哈夫曼树中的结点
typedef struct HTNode
{char val;int weight;struct HTNode * parent;       //双亲结点struct HTNode *lchild;       //左孩子结点struct HTNode *rchild;       //右孩子结点
}HTree,*HTnode;
/*如果为了简单，我们可以把结点值存储为int型，这样可以直接代替权重*///创建一个结点
HTree *creatennode(int weight,char value){HTnode node=(HTnode)malloc(sizeof(HTree));node->val=value;node->weight=weight;node->lchild = NULL;node->rchild = NULL;node->parent = NULL;return node;
}// 比较函数，用于对节点按照权重从小到大排序
int cmp(const void* a, const void* b) {HTnode node1 = *(HTnode*)a;HTnode node2 = *(HTnode*)b;return node1->weight - node2->weight;
}//构造哈夫曼树
HTree *createHTree(int n,char values[],int weights[]){HTnode *nodes = (HTnode*)malloc(sizeof(HTnode)*n);          //建立一个结点数组for (int i = 0; i < n; ++i) {nodes[i] = creatennode(weights[i], values[i]);          //给每一个结点赋值}while (n > 1) {// 对节点按照权重从小到大排序qsort(nodes, n, sizeof(HTnode), cmp);             //C语言的排序函数// 取出两个权重最小的节点构造一个新的父节点HTnode parent = creatennode(nodes[0]->weight + nodes[1]->weight, '-');  //构造它们的和结点，修改左右指针parent->lchild = nodes[0];parent->rchild = nodes[1];// 将新节点插入到原来的节点集合中，并将原来的两个子节点从集合中删除nodes[0] = parent;             for (int i = 2; i < n; ++i) {            //其实这并不是严格的删除操作，相当于数组0号元素重载，然后从2号元素开始向前移动一个位置nodes[i - 1] = nodes[i];}n--;}HTnode root = nodes[0];              //当剩下最后一个结点时，就是我们的根结点free(nodes);return root;
}
/*这里为了检验我们的哈夫曼树是否正确，就把它当作二叉树遍历出来，和我们的手算作比较*/
//遍历就不要多说了，参考我上一篇博客，二叉树的相关操作void visit1(HTnode &T){printf("%d\t",T->weight);             //这里遍历本来应该是输出value的，但是在构造二叉树的时候我们创建了新结点，其值是占位符，所以这里选择打印权值
}//这里我们采用先序遍历
void Preorder(HTnode &T){if(T!=NULL){visit1(T);        //在访问函数里面定义我们想要的可视化输出Preorder(T->lchild);Preorder(T->rchild);}
}//根据哈夫曼树输出哈夫曼编码
void print_code(HTnode &node, int* code, int len) {// 如果是叶子节点，打印它的字符和对应编码if (node->lchild == NULL && node->rchild == NULL) {printf("%c的哈夫曼编码: ", node->val);for(int i=0;i<len;i++){printf("%d ",code[i]);}printf("\n");}else {// 递归左子树，在编码末尾加上'0'code[len] = 0;print_code(node->lchild, code, len+1);// 递归右子树，在编码末尾加上'1'code[len] = 1;print_code(node->rchild, code, len+1);}
}int main(){int n;HTnode p;printf("请输入要编写的结点总数:");scanf("%d",&n);char values[n];int weights[n];for(int i=0;i<n;i++){printf("请输入第%d个结点的值:\n",i);scanf(" %c",&values[i]);        //这里%c前面一定要留一个空格抵消前面的换行，否则会出bug}for(int j=0;j<n;j++){printf("请输入第%d个元素的权重:\n",j);scanf("%d",&weights[j]);}p=createHTree(n,values,weights);Preorder(p);printf("\n");//到这一步，我已经测试了一遍，没有问题，下面开始思考哈夫曼编码问题int code[n]; // 初始化为空串print_code(p, code, 0);  // htree为哈夫曼树的根节点return 0;
}

代码虽然少，主要是写的过程。

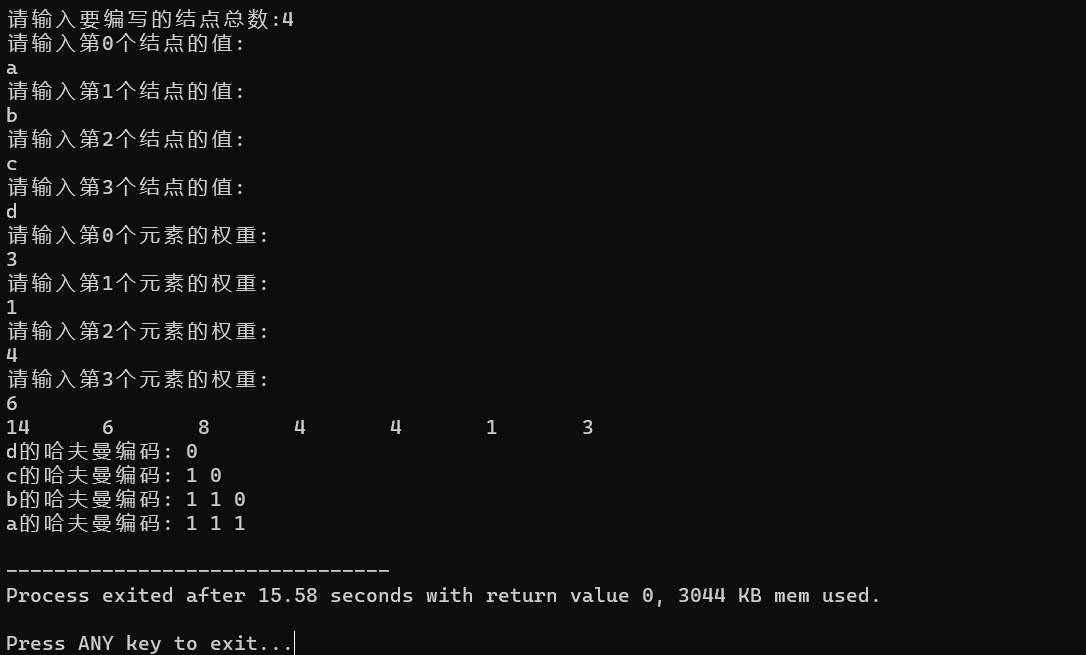
六.运行结果

9VTf.jpg


http://www.ppmy.cn/news/340134.html

相关文章

南卡和UHB电容笔哪款好用？国产平替电容笔对比

南卡和UHB电容笔哪款好用？国产平替电容笔对比

现在几乎每一人都有一款iPad设备&#xff0c;可以解决很多工作和学习上的问题&#xff0c;比如在办公室里处理文件&#xff0c;做一些简单的PPT&#xff0c;比如在学习的时候&#xff0c;记录一些笔记。如果直接用手指在ipad上打字&#xff0c;会让网页变得不整洁&#xff0c;不…
阅读更多...
性价比高的学生用台灯哪款好？推荐最适合学生用的台灯

性价比高的学生用台灯哪款好？推荐最适合学生用的台灯

“书山有路勤为径&#xff0c;学海无涯苦作舟”&#xff0c;读书是孩子们成长的必由之路&#xff0c;读书能够让孩子静下心来、拓宽知识面、获得更多的人生认知和看法。学习台灯其实市面上挺多&#xff0c;但是专为阅读而设计的台灯却并不多见。 1、南卡护眼台灯pro NANK南卡护…
阅读更多...
【安全运维】小微企业的安全运维工具用哪款好？

【安全运维】小微企业的安全运维工具用哪款好？

即使是小微企业&#xff0c;也同样面临着安全运维的困扰&#xff0c;同样面临着数据泄露、资产难管理的问题&#xff0c;因此选择一款合适的安全运维工具是非常必要的。那你知道小微企业的安全运维工具用哪款好&#xff1f; 小微企业的安全运维工具用哪款好&#xff1f; 【回…
阅读更多...
TWS无线蓝牙耳机哪款好用？入耳式蓝牙耳机排行榜

TWS无线蓝牙耳机哪款好用？入耳式蓝牙耳机排行榜

由于目前一些智能手机制造商为了让自己的产品能够更加强大&#xff0c;正在从手机上移除 3.5 毫米耳机端口&#xff0c;并且这已经成为了一种趋势&#xff0c;这也就导致目前无线耳机的需求量很大。现在&#xff0c;如果你想购买一款符合自己的无线耳机&#xff0c;那么下面这几…
阅读更多...
蓝牙耳机哪款好用音质好？高音质的蓝牙耳机推荐

蓝牙耳机哪款好用音质好？高音质的蓝牙耳机推荐

蓝牙耳机能够让我们享受自己喜欢的音乐&#xff0c;播客或有声读物&#xff0c;蓝牙技术越来越成熟&#xff0c;蓝牙耳机音质早就能和有线耳机媲美了&#xff0c;那么市面上有哪些好用的蓝牙耳机呢&#xff1f;下面我们一起来看看吧&#xff01; 一、南卡小音舱蓝牙耳机 动圈…
阅读更多...
入耳式无线蓝牙耳机哪款好用？入耳无线蓝牙耳机推荐

入耳式无线蓝牙耳机哪款好用？入耳无线蓝牙耳机推荐

蓝牙耳机在 AirPods推出之后&#xff0c;才开始大放异彩&#xff0c;真无线蓝牙耳机&#xff0c;让所有人都见识到了它的强大之处&#xff0c;可以实现无线连接&#xff0c;无论是随身携带&#xff0c;还是使用&#xff0c;都有很大的优势&#xff0c;下面我们就给你介绍一些比…
阅读更多...
【React】: React 脚手架初始化项目

【React】: React 脚手架初始化项目

一共只有两步。 1.初始化项目 npx create-react-app my-app2.启动项目&#xff0c;在项目根目录当中执行&#xff1a; cd my-appnpm start
阅读更多...
ISO21434 操作和维护(十)

ISO21434 操作和维护(十)

目录 一、概述 二、目标 三、网络安全事件响应 3.1 输入 3.1.1 先决条件 3.1.2 进一步支持信息 3.2 要求和建议 3.3 输出 四、更新 4.1 输入 4.1.1 先决条件 4.1.2 进一步支持信息 4.2 要求和建议 4.3 输出 一、概述 本条款描述了对文件中的项目…
阅读更多...
最新文章

Copyright @ 2022~2023