LeetCode - 1723 完成所有工作的最短时间

题目来源

题目描述

示例

提示

题目解析

算法源码

题目来源

1723. 完成所有工作的最短时间 - 力扣（LeetCode）

题目描述

给你一个整数数组 jobs ，其中 jobs[i] 是完成第 i 项工作要花费的时间。

请你将这些工作分配给 k 位工人。所有工作都应该分配给工人，且每项工作只能分配给一位工人。工人的工作时间是完成分配给他们的所有工作花费时间的总和。请你设计一套最佳的工作分配方案，使工人的最大工作时间得以最小化。

返回分配方案中尽可能最小的最大工作时间。

示例

输入	jobs = [3,2,3], k = 3
输出	3
解释	给每位工人分配一项工作，最大工作时间是 3 。

输入	jobs = [1,2,4,7,8], k = 2
输出	11
解释	按下述方式分配工作： 1 号工人：1、2、8（工作时间 = 1 + 2 + 8 = 11） 2 号工人：4、7（工作时间 = 4 + 7 = 11）最大工作时间是 11 。

提示

1 <= k <= jobs.length <= 12
1 <= jobs[i] <= 10^7

题目解析

我这里举个例子，来转换下本题的说法：

k个工人就是k个桶。

每个job就是一个高度为job的圆饼。

现在我们可以将jobs中的圆饼，全部放到k个桶中，那么每个桶中圆饼都有个累计高度，本题相当于求这个所有桶中圆饼累计高度的最低值是多少？

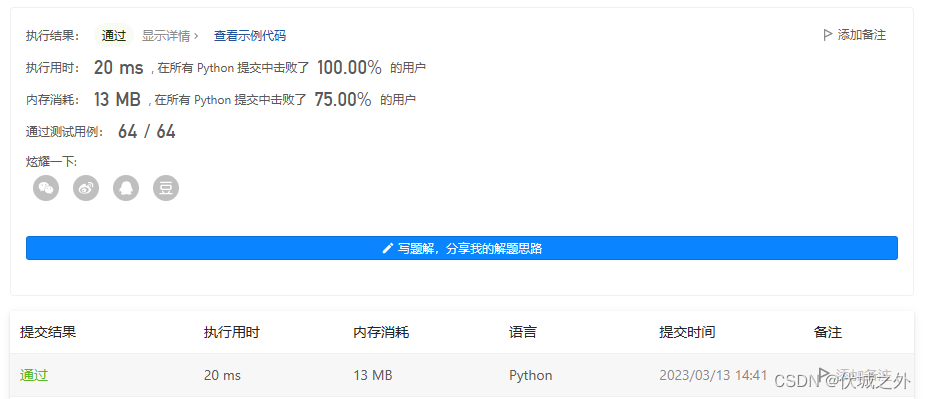
比如下图是用例2图示，这里最高高度的最低值就是11。

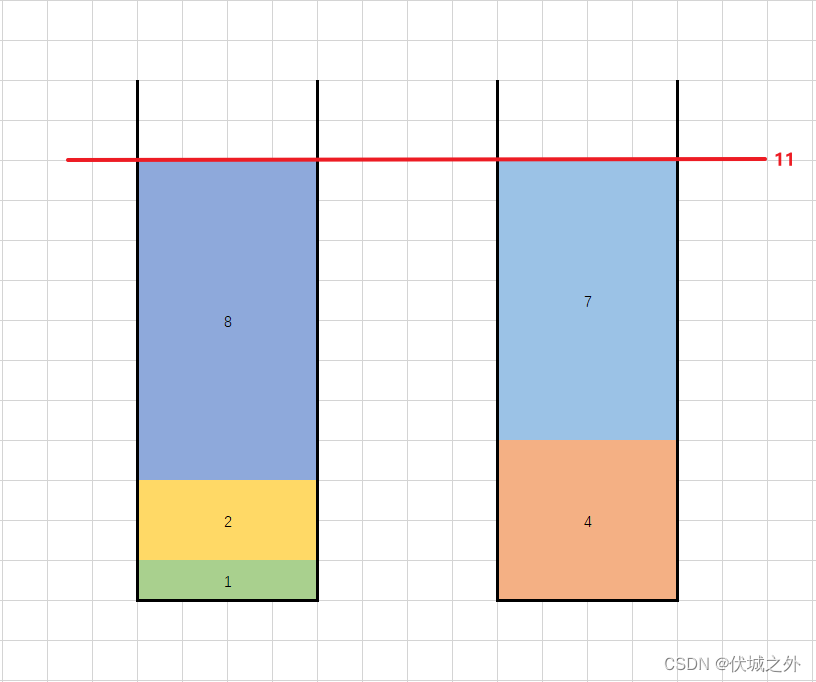
其他情况的高度都会高于这个值。

本题的最优解题思路是：二分法 + 回溯

其中二分法用于求解最低高度值，回溯算法用于验证二分求得的最低高度值是否符合要求。

二分法用于求解可能的最低累积高度值，这里必然有一个上下界高度值问题。

当所有圆饼全部放入一个桶中时，那么此时该桶内圆饼的累积高度值就是最大可能的累积高度值。

当一个桶不放入一个圆饼时，此时该桶内圆饼的累积高度值0就是最低可能的累积高度值。

但是，这里关于最低的累积高度值的取值可以进行优化：

如果说，桶数量（工人数量）大于圆饼数量（job数量）,那么必然会产生空桶，此时最低的累积高度值能取到0。但是这种场景，我们也不需要进行二分。可以直接返回所有jobs中最大的那个作为题解。

如果说，桶数量（工人数量）少于圆饼数量（job数量），那么必然不能产生空桶，因为空置一个桶的话，绝对不可能得到题解。我们必然需要让每个桶都放入圆饼。因此，对于这种场景，使用二分法时，最低累积高度值不需要从0开始，那么从哪个值开始呢？

我们可以思考一下，如果某个桶只放一个圆饼的话，那么放哪个圆饼，可以让其他桶的累积高度值尽可能小呢？答案是该桶放入最高的圆饼，这样才能保证其他桶的累积高度值尽可能低。

因此，二分法的最低累积高度取值应该是max(jobs)，而最高累积高度取值应该是sum(jobs)。

关于二分法的初始边界就讲到这，接下来就是二分法取中间值mid作为目标累积高度值去验证了。

那么如果验证这个mid值是否符合要求呢？

此时，我们应该通过回溯算法，尝试将圆饼放入各个桶中，如果在放的过程中，某个桶的累积高度值超过了mid，那么该放置方式不正确，此时应该进行回溯，继续尝试其他放置方式。

如果所有的放置方式都不行，即都会产生某个桶中圆饼的累积高度超过mid值，那么此时可以判定mid值取小了。我们应该下次让mid变大一点，即让二分的左边界右移到mid+1位置。

如果存在某个放置方式，可以让所有圆饼放入各个桶中，且此时各个桶中圆饼的累积高度值都不会超过mid，此时说明当前mid值就是一个符合要求的，但是不一定是最优的。此时我们应该降低mid值继续尝试，即让二分的右边界左移到mid位置（PS：这里为什么不是mid-1位置呢？这个具体代码有关，我下面代码取最终的二分左边界为题解，如果代码取最终的二分右边界为题解，则此处可以是mid-1）。

以上就是回溯的逻辑，这个非常类似于LeetCode - 698 划分为k个相等的子集_伏城之外的博客-CSDN博客

另外本题回溯有一个重要的剪枝，那就是，如果回溯放圆饼到桶的过程中，出现了空桶，那么此时即使最终可以放置成功，也肯定不是最优解，因为我们只要把其他桶的圆饼放到空桶，则必然能产生更优解。因此回溯过程中，出现空桶，可以直接认定为不符合要求。

Java算法源码

import java.util.Arrays;class Solution {public int minimumTimeRequired(int[] jobs, int k) {if (jobs.length <= k) {int t = 0;for(int job : jobs) t = Math.max(t, job);return t;}int n = jobs.length;Arrays.sort(jobs);int min = jobs[n-1];int max = 0;for(int job : jobs) max += job;while (min < max) {int mid = (min + max) >> 1;if (check(n-1, jobs, new int[k], mid)) {max = mid;} else {min = mid + 1;}}return min;}public static boolean check(int index, int[] jobs, int[] buckets, int limit) {if (index < 0) {return true;}int select = jobs[index];for (int i = 0; i < buckets.length; i++) {if (select + buckets[i] <= limit) {buckets[i] += select;if (check(index - 1, jobs, buckets, limit)) return true;buckets[i] -= select;if (buckets[i] == 0) return false;}}return false;}
}

JavaScript算法源码

/*** @param {number[]} jobs* @param {number} k* @return {number}*/
var minimumTimeRequired = function(jobs, k) {if(jobs.length <= k) {return Math.max(...jobs)}jobs.sort((a,b) => b-a)let min = jobs[0]let max = jobs.reduce((a,b) => a+b);while(min < max) {let mid = Math.floor((min + max) / 2);const buckets = new Array(k).fill(0);if(check(0, mid, buckets, jobs)) {max = mid} else {min = mid + 1}}return min
};function check(index, limit, buckets, jobs) {if(index == jobs.length) {return true;}const select = jobs[index];for(let i=0; i<buckets.length; i++) {if(buckets[i] + select <= limit) {buckets[i] += select;if(check(index + 1, limit, buckets, jobs)) return true;buckets[i] -= select;if(buckets[i] == 0) return false;}}return false;
}

Python算法源码

class Solution(object): def minimumTimeRequired(self, jobs, k):""":type jobs: List[int]:type k: int:rtype: int"""if len(jobs) <= k:return max(jobs)def check(limit, index, buckets):if index == len(jobs):return Trueselect = jobs[index]for i in range(len(buckets)):if buckets[i] + select <= limit:buckets[i] += selectif check(limit, index + 1, buckets):return Truebuckets[i] -= selectif buckets[i] == 0:return Falsereturn Falsejobs.sort(reverse=True)low = jobs[0]high = sum(jobs)while low < high:mid = (low + high) >> 1buckets = [0]*kif check(mid, 0, buckets):high = midelse:low = mid + 1return low