1. 摘要
基于对比学习(CL)的自我监督学习模型以成对的方式学习视觉表征。虽然目前流行的CL模型已经取得了很大的进展,但在本文中,我们发现了一个一直被忽视的现象:当用完整图像训练CL模型时,在完整图像中测试的性能比在前景区域测试的性能要好;当使用前景区域训练CL模型时,在完整图像中测试的性能比在前景区域测试的性能差。这一观察结果表明,图像中的背景可能会干扰模型学习的语义信息,其影响尚未完全消除。为了解决这个问题,我们建立了一个结构因果模型(SCM),将背景建模为一个混淆剂。我们提出了一种基于后门调整的正则化方法,即基于元语义正则化的介入性对比学习(ICLMSR),对所提出的供应链管理进行因果干预。ICL-MSR可以整合到任何现有的CL方法中,以减轻表征学习的背景干扰。从理论上证明了ICL-MSR具有更小的误差范围。经验上,我们在多个基准数据集上的实验表明,ICL-MSR能够提高不同最先进的CL方法的性能。
2. 动机
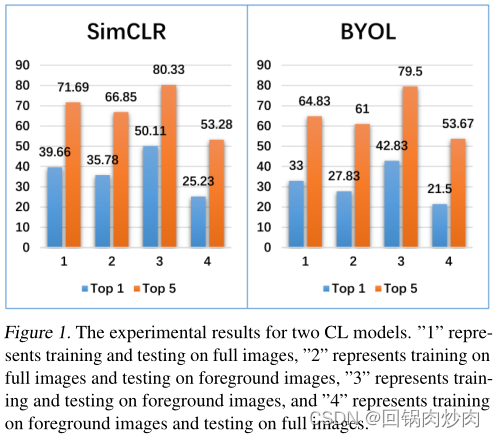
COCO数据集上四种实验设置
- 在完整图像上训练和测试CL模型;
- 分别在完整图像和前景图像上训练和测试CL模型;
- 在前景图像上训练并测试CL模型;
- 分别在前景图像和完整图像上训练和测试CL模型。
两个互斥的结论
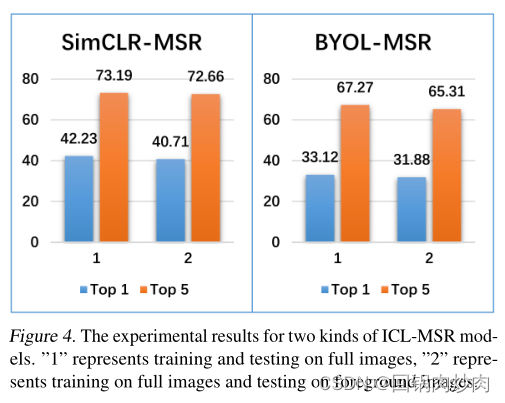
对比1和2可以发现,在完整图像上测试的性能优于在前景图像上测试的性能。此外,对比1和4可以发现,用完整图像训练的模型在完整图像上测试时优于用前景图像训练的模型。由此得出结论一——背景相关信息可以影响CL模型的学习过程。
对比3和4可以发现,使用前景图像训练模型时,在前景图像上的测试性能远高于在完整图像上测试的性能。而且,考虑所有变量发现,只使用前景图像训练和测试会产生最好的结果。由此得出结论二——背景相关信息会降低基于此的CL模型的性能。
合理的解释
一个经过完整图像训练的特征提取器可以提取与背景相关的语义特征。在测试阶段,由于整个图像同时包含前景部分和背景部分,除了前景部分,背景部分对分类也有一定的促进作用。另一方面,CL努力适应各种下游任务,如对象检测、对象分割等。只有与前景相关的语义信息才能保证学习到的特征对各种任务的鲁棒性。
主要贡献
- 发现了一个悖论:在不同的设置下,背景信息既可以提高也可以阻止学习到的特征表示性能的提高。
- 为了捕捉语义信息、正样本和锚点之间的因果关系,我们建立了一个结构因果模型(SCM)。我们可以简单地推断,背景是一个有效的混淆器,在正样本和基于此的锚之间产生误导的相关性。
- 我们提出了一种新的方法,称为介入性对比学习与元语义正则化(ICL-MSR),通过实施后门调整计划的SCM。
- 我们提供了误差范围的理论保证和经验评价,以证明ICLMSR可以改善不同的先进的CL方法的性能。
3. 定义
3.1 结构因果模型
最小化式1可以近似等价于预测 X i 3 − j X^{3-j}_i Xi3−j到标签 X i j X^j_i Xij。然后,CL中涉及的SCM可以形式化为图2。
SCM中的节点表示抽象的数据变量,而有向边表示(函数)因果关系,例如: X i 3 − j → Y ( X i 3 − j ) X^{3-j}_i \rightarrow Y(X^{3-j}_i) Xi3−j→Y(Xi3−j)代表 X i 3 − j X^{3-j}_i Xi3−j是原因, Y ( X i 3 − j ) Y(X^{3-j}_i) Y(Xi3−j)是结果。
图二解释
- X i 3 − j → Y ( X i 3 − j ) X^{3-j}_i \rightarrow Y(X^{3-j}_i) Xi3−j→Y(Xi3−j): Y ( X i 3 − j ) Y(X^{3-j}_i) Y(Xi3−j)表示 X i 3 − j X^{3-j}_i Xi3−j对应的标签。在这里标签等价于锚点,因此有 Y ( X i 3 − j ) = X i j Y(X^{3-j}_i)=X^{j}_i Y(Xi3−j)=Xij。该链接假设 X i 3 − j X^{3-j}_i Xi3−j应该与 X i j X^{j}_i Xij相似。
- X i 3 − j ← X s → Y ( X i 3 − j ) X^{3-j}_i \leftarrow X_s \rightarrow Y(X^{3-j}_i) Xi3−j←Xs→Y(Xi3−j): X s X_s Xs表示语义信息,可以认为是特征提取器 f f f的卷积核。因此,链接 X i 3 − j ← X s X^{3-j}_i \leftarrow X_s Xi3−j←Xs和 X s → Y ( X i 3 − j ) X_s \rightarrow Y(X^{3-j}_i) Xs→Y(Xi3−j)假设 X i 3 − j X^{3-j}_i Xi3−j和 Y ( X i 3 − j ) Y(X^{3-j}_i) Y(Xi3−j)在潜在空间中的特征表示是用 f f f提取的,每个特征表示通道对应一个语义信息。
- 为了寻找 X i 3 − j X^{3-j}_i Xi3−j和 Y ( X i 3 − j ) Y(X^{3-j}_i) Y(Xi3−j)之间真正的因果关系,我们需要用因果干预器 P ( Y ( X i 3 − j ) ∣ d o ( X i 3 − j ) ) P(Y(X^{3-j}_i)|do(X^{3-j}_i)) P(Y(Xi3−j)∣do(Xi3−j))来替代 P ( Y ( X i 3 − j ) ∣ X i 3 − j ) P(Y(X^{3-j}_i)|X^{3-j}_i) P(Y(Xi3−j)∣Xi3−j)衡量因果关系。
3.2 通过后门调整进行因果干预
特征提取器能够提取与背景相关语义特征的原因
- 正样本数量太少只有一个
如目标式1所示,随机给定一个锚点,只有一个正样本,但有 2 N − 2 2N-2 2N−2个负样本。此外,在负对中有一些样本(假负样本)与正样本具有相同的前景。而正对中的锚点和样本是由相同的原始图像生成的,使得两个正样本之间的前景和背景相似。在最小化目标式1时,如果正样本太少,正样本对之间共享的前景和背景可能会一起将正样本拖向锚点。还对与锚具有相同语义信息的假负样本进行观察。因此,将假负样本从锚点移远,主要是降低前景相似度。也就是说,这在一定程度上可能促使 “拖拽” 操作更加重视的背景。因此,背景的作用得到了增强。这就使得以往的对比学习模型能够提取与背景相关的语义特征。
后门调整
后门调整假设我们可以观察和分层混淆。在提出的SCM中,混淆器包含在 X s X_s Xs中,我们可以将其分层为不同的语义特征,例如: X s = { Z s i } i = 1 i = n X_s=\{Z^i_s\}^{i=n}_{i=1} Xs={Zsi}i=1i=n,其中 Z s i Z^i_s Zsi表示语义特征的分层。形式上,SCM的后门调整如下所示:
其中 P ( Y ( X i 3 − j ) ∣ d o ( X i 3 − j ) ) P(Y(X^{3-j}_i)|do(X^{3-j}_i)) P(Y(Xi3−j)∣do(Xi3−j))表示 X i 3 − j X^{3-j}_i Xi3−j和 Y ( X i 3 − j ) Y(X^{3-j}_i) Y(Xi3−j)之间的真实因果关系。
4. 方法
4.1 元语义正则化
为了不失一般性,我们将特征提取器 f f f的输出 Z i j Z^j_i Zij的维数表示为 w × h × c w×h×c w×h×c,其中 w w w为宽度, h h h为高度, c c c为特征通道数。更具体地说,我们记 Z i j Z^j_i Zij为 Z i j = [ Z i , 1 j , . . . , Z i , c j ] Z^j_i=[Z^j_{i,1},...,Z^j_{i,c}] Zij=[Zi,1j,...,Zi,cj],其中 Z i , r j ∈ R w × h Z^j_{i,r} \in R^{w×h} Zi,rj∈Rw×h表示 Z i j , r ∈ { 1 , . . . , c } Z^j_i,r\in \{1,...,c\} Zij,r∈{1,...,c}。
注意:对于任何预先训练的基于CNN的特征提取器,每个通道对应一种语义信息或视觉概念。然而,用单个通道编码一个视觉概念是很困难的。因此,这促使我们为每个语义信息寻找一个权重向量。我们的想法是,每个语义信息对应于通道的一个子集。因此,这个相关通道子集的权值应该很大,而子集之外的通道的权值应该很小。
给定一个权向量 a t = [ a 1 , t , . . . , a c , t ] T a_t=[a_{1,t},...,a_{c,t}]^T at=[a1,t,...,ac,t]T,我们表示 Z s t Z^t_s Zst的函数实现为 Z s t = a t Z^t_s=a_t Zst=at,和 P ( Z s t ) = 1 / n P(Z^t_s)=1/n P(Zst)=1/n。然后,我们表示 P ( Y ( X i 3 − j ) ∣ X i 3 − j , Z s t ) P(Y(X^{3-j}_i)|X^{3-j}_i,Z^t_s) P(Y(Xi3−j)∣Xi3−j,Zst)的函数实现为:
其中 a t ⊙ Z i 3 − j = [ a 1 , t ⋅ Z i , 1 3 − j , . . . , a c , t ⋅ Z i , c 3 − j ] a_t\odot Z^{3-j}_i=[a_{1,t}·Z^{3-j}_{i,1},...,a_{c,t}·Z^{3-j}_{i,c}] at⊙Zi3−j=[a1,t⋅Zi,13−j,...,ac,t⋅Zi,c3−j]。因此,整体后门调整情况为:
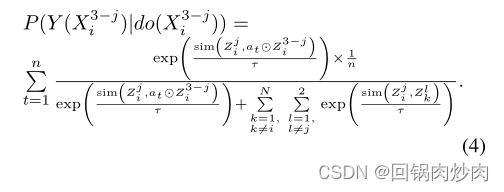
提出的元语义正则化器可以看作是一个可学习的模块 f m s r f_{msr} fmsr,该模块生成语义相关的权值矩阵 A s A_s As,并通过卷积神经网络实现,其中 A s = [ a 1 , . . . , a n ] A_s=[a_1,...,a_n] As=[a1,...,an]。体来说,对于一个输入样本 X X X,我们首先得到两个增广样本 { X 1 , X 2 } \{X^1, X^2\} {X1,X2}将 X X X输入到一个随机数据增强模块。然后将 X X X输入 f m s r f_{msr} fmsr模块,得到权重矩阵 A s A_s As,两个增广样本 { X 1 , X 2 } \{X^1, X^2\} {X1,X2}只有一个权重矩阵 A s A_s As。
4.2 模型目标
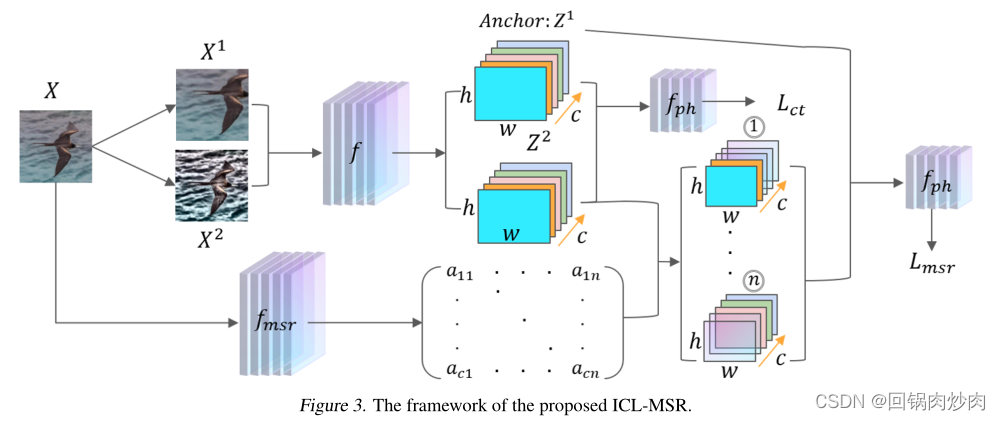
ICL-MSR由特征提取器 f f f、元语义正则化器 f m s r f_{msr} fmsr和投影头 f p h f_{ph} fph三个模块组成。元语义正则化器与特征提取器一起训练,每个时期有两个阶段。第一阶段使用两个增强训练数据集 X t r a u g X^{aug}_{tr} Xtraug和语义相关权矩阵 A s A_s As学习 f f f和 f p h f_{ph} fph。在第二阶段,通过计算 f m s r f_{msr} fmsr相对于对比损失的梯度来更新 f m s r f_{msr} fmsr。
在每个epoch的第一阶段,通过最小化目标 L t o L_{to} Lto来更新 f f f和 f p h f_{ph} fph的参数,可以表示为:
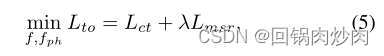
其中 L c t L_{ct} Lct为目标1, λ \lambda λ为超参数, L m s r L_{msr} Lmsr为:
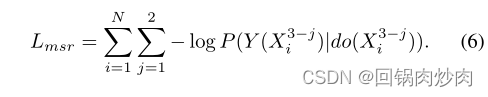
在每个阶段的第二阶段,为了学习 f m s r f_{msr} fmsr的参数,我们提出了一个基于元学习的训练机制。也就是说, f m s r f_{msr} fmsr通过选择权重矩阵来更新,如果使用权重矩阵训练 f f f和 f p h f_{ph} fph,初级对比学习的性能将在相同的训练数据上最大化。具体来说,我们首先用学习率 α α α更新 f f f和 f p h f_{ph} fph一次,方法如下:
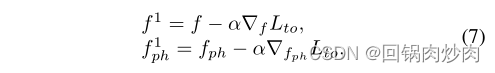
这两个更新可以看作是学习了一个好的 f f f和一个好的 f p h f_{ph} fph。经过这一步, f 1 f^1 f1和 f p h 1 f^1_{ph} fph1可以看作是 f m s r f_{msr} fmsr的函数,因为 ∇ f L t o ∇_fL_{to} ∇fLto和 ∇ f p h L t o ∇_{f_{ph}}L_{to} ∇fphLto与 f m s r f_{msr} fmsr有关。然后,我们通过最小化以下内容来更新 f m s r f_{msr} fmsr:
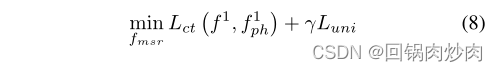
其中 γ γ γ是超参数, L c t ( f 1 , f p h 1 ) L_{ct}(f^1, f^1_{ph}) Lct(f1,fph1)表示损失 L c t L_{ct} Lct是基于参数 f 1 f^1 f1和 f p h 1 f^1_{ph} fph1计算的,而 L u n i L_{uni} Luni是均匀损失,旨在约束 A s A_s As中元素的分布,以近似均匀分布,从而产生的视觉语义可以尽可能不一致。基于高斯势核, L u n i L_{uni} Luni可以表示为:
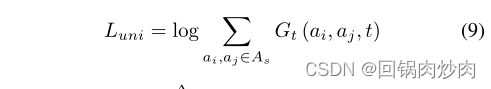
式中 G t ( a i , a j , t ) ≜ e x p ( 2 t ⋅ a i T a j − 2 t ) G_t(a_i,a_j,t)\triangleq exp(2t·a_i^Ta_j−2t) Gt(ai,aj,t)≜exp(2t⋅aiTaj−2t), t t t为固定超参数。
问题是最小化目标8为什么可以使 f m s r f_{msr} fmsr学习语义信息。需要注意的是,只有正对之间共享的语义信息才能提示 X i 3 − j X^{3−j}_i Xi3−j和 Y ( X i 3 − j ) Y(X^{3−j}_i) Y(Xi3−j)相似,从而最小化对比损失。通过SCM可以看出,共享的语义信息包含了背景信息和前景信息。目标8背后的思想是最小化对比损失,以便 f m s r f_{msr} fmsr学习共享的语义信息。这一步也可以看作是在 L c t L_{ct} Lct的基础上再一次促进 L c t L_{ct} Lct的学习,类似于学习学习。这也是我们称它为元语义正则化器的原因。
5. 下游分类的误差界
分类任务经常被用来评价大多数的语言学习方法的性能。因此,我们提出了基于通过最小化传统交叉熵损失来训练softmax分类器的分类任务的ICL-MSR泛化误差界(GEB)。例如 L S M ( f ; T ) = i n f W L C E ( W ⋅ f ; T ) L_{SM}(f;T) = inf_WL_{CE}(W·f;T) LSM(f;T)=infWLCE(W⋅f;T),其中 W W W为线性分类器, T T T为标签。对于特征嵌入 f ( X ) f(X) f(X),泛化误差由 L S M T ( f ) = E X [ L S M ( f ; T ) ] L^T_{SM}(f) = E_X[L_{SM}(f;T)] LSMT(f)=EX[LSM(f;T)]。然后我们研究了这种泛化误差 L S M T ( f ) L^T_{SM}(f) LSMT(f)与对比学习目标 L c t L_{ct} Lct之间的差距。
定理5.1
令 f ∗ ∈ a r g m i n f L c l + λ L m s r f^*\in argmin_fL_{cl}+\lambda L_{msr} f∗∈argminfLcl+λLmsr。那么至少有 1 − δ 1−δ 1−δ的概率
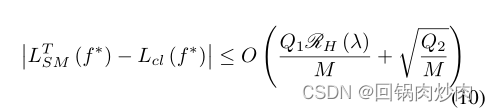
其中M为训练样本总数,N为小批量的大小, Q 1 = 1 + 1 / N , Q 2 = l o g ( 1 / δ ) ⋅ l o g 2 ( M ) Q_1=\sqrt {1 + 1/N},Q_2 = log (1/δ)·log^2 (M) Q1=1+1/N,Q2=log(1/δ)⋅log2(M), R H ( λ ) R_H (λ) RH(λ)为Rademacher复杂度。同时, R H ( λ ) R_H (λ) RH(λ)与 λ λ λ呈单调递减关系。
如式10所示,我们可以得到误差界随着训练样本大小M的增加而逐渐减小。注意,这个观察结果与传统的监督学习方法是一致的。此外,我们可以看到误差项 Q 2 / N \sqrt{Q_2/N} Q2/N中的小批量大小N对于大样本大小N是可以忽略的,在这种情况下,相对大的尺寸N将有效地减少第一误差项 Q 1 R H ( λ ) Q_1R_H (λ) Q1RH(λ),从而收紧误差界。最后,当我们扩大正则化参数λ时,Rademacher复杂度 R H R_H RH也会降低,从而进一步减小了误差界,提高了对比学习算法的泛化性。
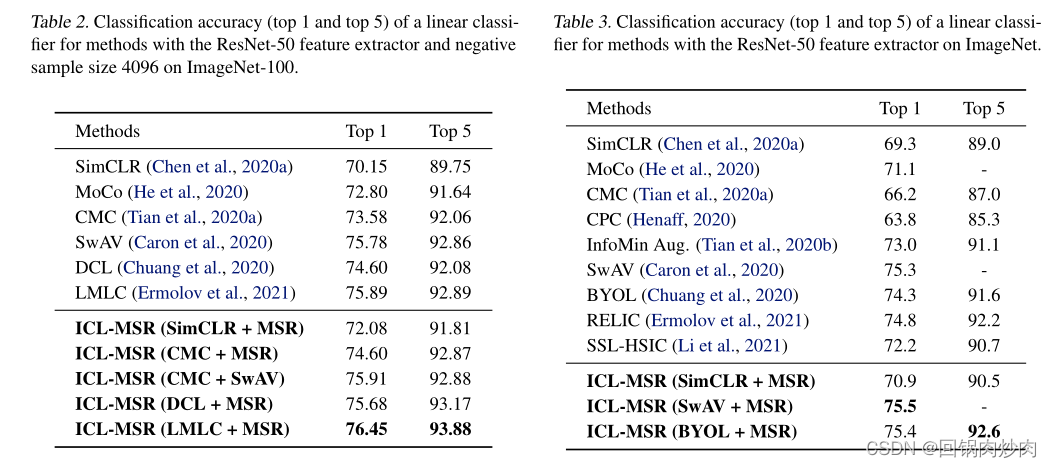
6. 实验结果