#include<algorithm>
#include<cstdio>
#define ll long long
using namespace std;
const int N=1e5+5;
const ll inf=1e14+5;
int n,m,b[N],id[N];
ll a[N],q[N],dp[205][N];
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&a[i]);a[i]+=a[i-1];}for(int i=1;i<=m;i++)scanf("%d",&b[i]);for(int i=1;i<=m;i++)for(int j=1;j<=n;j++)dp[i][j]=-inf;for(int i=b[m];i<=n;i++)if(m&1)dp[m][i]=a[i]-a[i-b[m]];elsedp[m][i]=a[i-b[m]]-a[i]; for(int i=m-1;i>=1;i--){int L=1,R=0;id[0]=0;if(i&1)for(int j=i-1+b[i];j<=n-i+1;j++){int l=j-b[i]+b[i+1]+1,r=j-1;for(int k=id[R]+1;id[R]<r;k++)if(dp[i+1][k]!=-inf){while(R>=L&&q[R]>=dp[i+1][k])R--;q[++R]=dp[i+1][k];id[R]=k;}while(L<=R&&id[L]<l)L++;if(L<=R)dp[i][j]=q[L]+(a[j]-a[j-b[i]]);}elsefor(int j=i-1+b[i];j<=n-i+1;j++){int l=j-b[i]+b[i+1]+1,r=j-1;for(int k=id[R]+1;id[R]<r;k++)if(dp[i+1][k]!=-inf){while(R>=L&&q[R]<=dp[i+1][k])R--;q[++R]=dp[i+1][k];id[R]=k;}while(L<=R&&id[L]<l)L++;if(L<=R)dp[i][j]=q[L]-(a[j]-a[j-b[i]]);}}ll ans=-inf;for(int i=b[1];i<=n;i++)ans=max(ans,dp[1][i]);printf("%lld\n",ans);return 0;
}
游戏(game)
news/2024/10/30 17:25:46/
相关文章
你今天玩游戏了吗?游戏道具了解下
【面试题】 某游戏的某促销活动,会向玩家推荐一个道具,同时会得到该道具的折扣券。折扣券无有效期,但购买道具一次后失效。推荐一个新的道具,也会导致旧的折扣券失效。 假设道具推荐、查看、购买行为记录在了下面的“游戏道具记录…
Nim 游戏 、⽯头游戏1、石头游戏2
Nim 游戏 、⽯头游戏1、石头游戏2 文章目录 Nim 游戏 、⽯头游戏1、石头游戏2**一:Nim 游戏****二:⽯头游戏****三、石头游戏2****方法一:DP 函数****方法二:DP table** 一:Nim 游戏
你和你的朋友,两个人一…
这有10款好玩游戏,游戏迷速来围观
1、我飞刀玩得贼6
一款创新玩法的游戏,通过对一大堆飞刀的熟练操控来进行混战,独创的龟缩防御机制,让你能轻松在对手面前秀一把。 2、监狱建筑师
它作为一款优秀的模拟游戏,沿袭了《地下城守护者》、《矮人要塞》以及《主题医院…
从0-1一起学习live555设计思想之二 RTSP交互过程
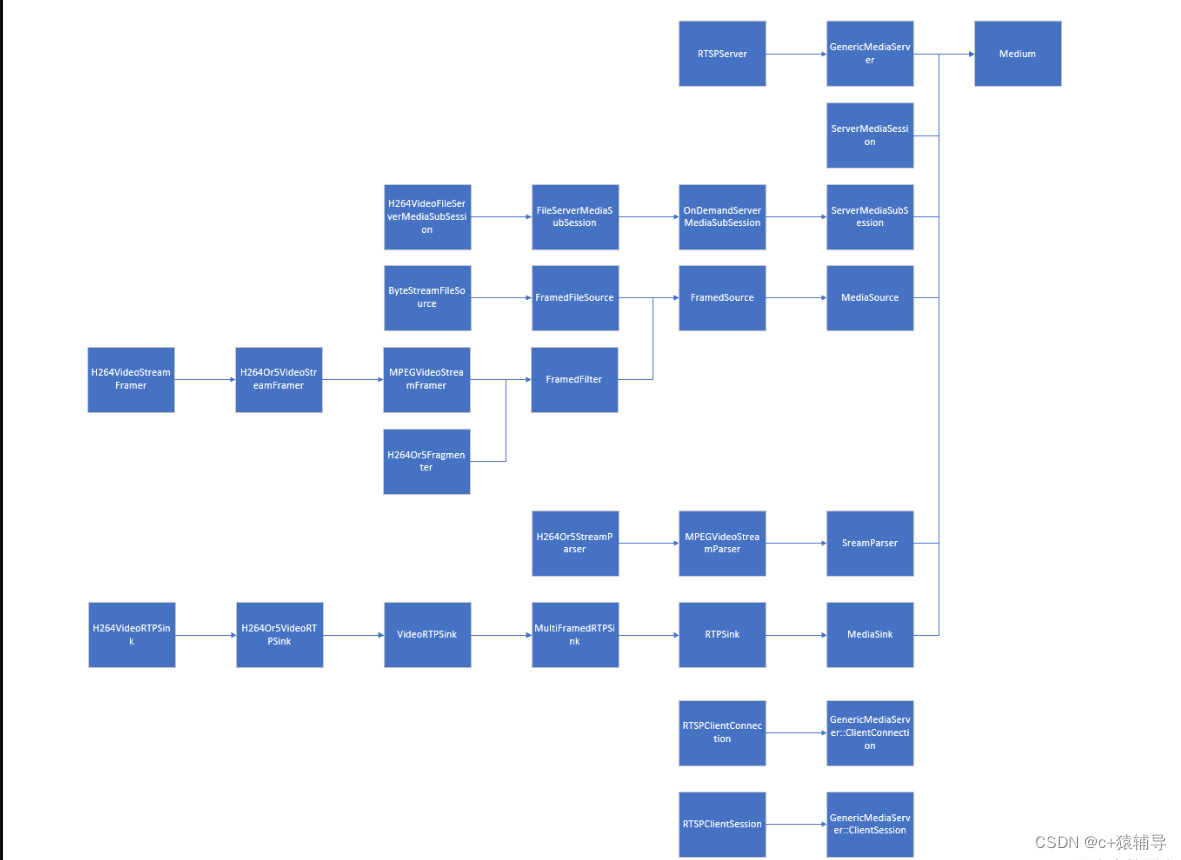
流媒体服务系列 文章目录 流媒体服务系列前言一、OPTION二、DESCRIBE三、SETUP四、PLAY总结前言
本篇文章通过代码去分析rtsp交互过程与工作原理。由于live555的继承关系太过复杂,所以做了个图简单记录一下与h264文件传输相关的类继承关系。 一、OPTION
OPTION比较简单,就…
C语言基础--整型int,长整型long,浮点型double float
本文讲解常见的C语言变量,并举出一些实例
从微软的C语言文档把所有的C语言可定义(就是能用的)截图展示: 还有好几页,不放了,看着都头疼 但是,往往用的最多的,也就是下面的(本篇只讲整数和浮点数)
int 整数 整数的定义不用说了吧QAQ int a = 10; //定义一个…
libVLC 调节图像(亮度、对比度、色调、饱和度、伽玛)
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 对于一个视频来说,色彩和画面效果的呈现非常重要。假如你的画面偏暗或偏亮,缺乏层次感,色彩不够丰富或不自然,则需要根据场景和氛围进行调整。 所涉及的重要参数有: 亮度: 是视频画面的明暗程度。调整…
shell脚本基础5——常用命令写作技巧
文章目录 一、grep命令二、sed命令2.1 选项参数2.2 常用命令 三、AWK命令3.1 常用参数3.2 常用示例 四、find与xargs五、date命令六、对话框6.1 消息框6.2 yes/no对话框6.3 表单输入框6.4 密码输入框6.5 菜单栏6.6 单选对话框6.7 多选对话框6.8 进度条 七、常用写作技巧7.1 EOF…
做副业的我很迷茫,但ChatGPT却治好了我——AI从业者被AI模型治愈的故事
迷茫,无非就是不知道自己要做什么,没有目标,没有方向。 当有一个明确的目标时,往往干劲十足。但做副业过程中,最大的问题往往就是 不知道自己该干什么。 干什么?怎么干?干到什么程度?…