前言

        优先级队列听名字好像与队列有关，但是实际上，与队列没有很多关系，它也是容器适配器，是通过vector来适配的，但是里面又加入了堆的调整算法。跟栈和队列又有一些不同，了解它的实现对于我们更好的掌握它是有一定的帮助的。 

目录

1.完整代码

2.向上调整算法

3.向下调整算法

4.仿函数

5.测试代码 

---

1.完整代码

namespace qyy
{//less是小于，但是确默认生成的是大堆template<class T,class container = vector<T>,class compare = less<T>>class priority_queue{public://向下调整算法void AdjustDown(int root,int Size)//闭区间{int chird = root * 2 + 1;while (chird<= Size)//孩子到最后一个叶子节点就可以结束了{//确定孩子中较大的哪个if (chird+ 1 <= Size&& _com(_con[chird] , _con[chird+1])  )//chird+1要在数组的范围内比较才有意义++chird;//找出孩子中值大的那个，然后进行比较//比较root和chird//if (pq[chird] > pq[root])//交换if(  _com(_con[root] , _con[chird])  ){swap(_con[chird], _con[root]);//迭代往后继续比较root = chird;chird = root * 2 + 1;}else{break;}}}//向上调整算法void AdjustUp(int chird){int parent = (chird - 1) / 2;while (parent>= 0)//继续调整{//if (pq[parent] < pq[chird])//父亲比孩子小if(_com(_con[parent],_con[chird])){//交换swap(_con[parent], _con[chird]);//迭代继续chird = parent;parent = (chird - 1) / 2;}else {break;//不要交换直接结束程序}}}void push(const T& data){_con.push_back(data);//先尾插//在向上调整AdjustUp(_con.size()-1);}void pop(){//先将最大和末尾的进行交换swap(_con[0], _con[_con.size() - 1]);//删除队尾元素_con.pop_back();//向下调整AdjustDown(0,_con.size()-1);}size_t size(){return _con.size();}bool empty(){return _con.empty();}T& top(){return _con.front();}private:container _con;compare _com;};
}
//仿函数 仿函数又叫函数对象
namespace qyy
{template<class T>struct less{bool operator()(const T& num1,const T& num2){return num1 < num2;}};template<class T>struct greater{bool operator()(const T& num1, const T& num2){return num1 > num2;}};
}

        这里的底层容器和仿函数都给了缺省参数，因为默认是大堆所以就给缺省的模板参数，也就是泛型编程。 

2.向上调整算法

        向上调整算法是在建堆时进行使用的，就是为了保证堆的性质，其实在物理结构上堆是一颗满二叉树 且分为大堆和小堆，大堆就是堆顶的数据大于堆底的数据，反映到二叉树上面就是，根节的值点大于左右子树，整个数都满足这个规律就是大堆了，反之如果根节点的值小于左右子树，且整个树都满足这个规律就是小堆了。如图：

因为堆是借助数组实现的所以看起来是这样的，其实可以看出下面这样：

 

        上面是一个大根堆，那么堆的向上调整算法是如何实现的呢？我们一起向下看：

          

         代码实现如下：

	    //向上调整算法void AdjustUp(int chird){int parent = (chird - 1) / 2;while (parent>= 0)//继续调整{//if (pq[parent] < pq[chird])//父亲比孩子小if(_com(_con[parent],_con[chird])){//交换swap(_con[parent], _con[chird]);//迭代继续chird = parent;parent = (chird - 1) / 2;}else {break;//不要交换直接结束程序}}}

        优先级队列push数据的时候是先push数据到vector中，然后使用向上调整算法来维持堆。 

3.向下调整算法

        在优先级队列pop数据的时候是先将堆顶的元素与堆底的元素交换数据，然后在删除堆底的元素，调用向下调整算法来维持堆的特性，因为优先级队列始终出队的是优先级最高的元素。

        向下调整算法首先从根节点开始，如果是建大堆，就将根节点与左右节点中较大的那个比较，如果左右节点中值较大的那个大于根节点的值就交换左右节点与根节点，更新根节点和左右节点的值，继续比较，知道比较的叶子节点的下标大于数组的值，我这样将可能太抽象了，就拿这组已经调整好了的数据来看看吧，

此时pop数据，先交换9和6，然后删除调数组末尾的9，从数组开头开始进行向下调整。如图：

 

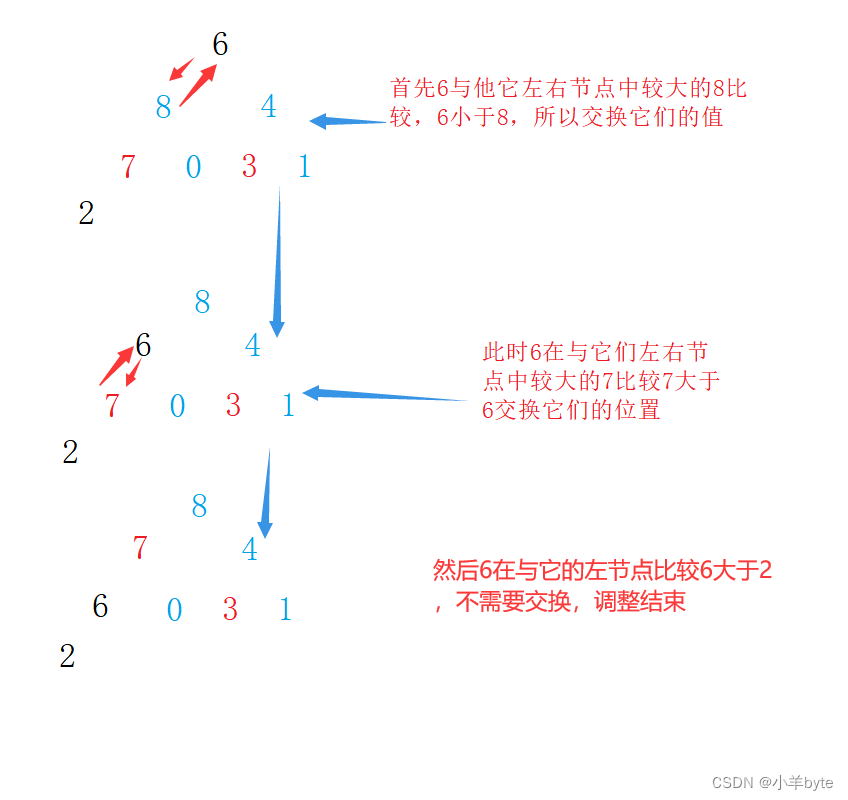
        实现代码：

	    //向下调整算法void AdjustDown(int root,int Size)//闭区间{int chird = root * 2 + 1;while (chird<= Size)//孩子到最后一个叶子节点就可以结束了{//确定孩子中较大的哪个if (chird+ 1 <= Size&& _com(_con[chird] , _con[chird+1])  )//chird+1要在数组的范围内比较才有意义++chird;//找出孩子中值大的那个，然后进行比较//比较root和chird//if (pq[chird] > pq[root])//交换if(  _com(_con[root] , _con[chird])  ){swap(_con[chird], _con[root]);//迭代往后继续比较root = chird;chird = root * 2 + 1;}else{break;}}}

 

4.仿函数

        仿函数也叫函数对象，这里我们实现的优先级队列，不管建大根堆还是小根堆，都只能实现一份，要是再去实现另一种的话如果在写一份相同的代码，只是比较的逻辑相反那么代码的冗余度就会很高，所以这里提供了第三个模板参数，用来解决这个问题。

template<class T,class container = vector<T>,class compare = less<T>> 

        我们在实现调整算法的时候将需要比较大小的地方单独拎出来，用第三个模板参数去实例化出一个对象，然后通过这个对象调用operator（） 来实现比较大小，如果我们传给模板的是比较小于为真的对象重载的operator（），那么就是数字大的优先级高，反之则相反，这里其实有个坑与正常的比较大小是相反的，至于为了写出这样的代码，这得问制定标准的大师了。正所谓前任挖坑后人跳坑。

        代码如下：

//仿函数 仿函数又叫函数对象
namespace qyy
{template<class T>struct less//比较大于{bool operator()(const T& num1,const T& num2){return num1 < num2;}};template<class T>struct greater//比较小于{bool operator()(const T& num1, const T& num2){return num1 > num2;}};
}

注意一般成员都是公有的采用struct定义类，如果成员一些公有一些私有采用class定义。

在使用STL中的sort时，默认排序排的都是升序，如果想要排降序就需要给它的缺省参数传一个仿函数，一般greater是排升序的，less是排降序的。

例如：

void test()
{vector<int>v1;v1.push_back(1);//对vector进行排序v1.push_back(6);v1.push_back(2);v1.push_back(3);v1.push_back(5);v1.push_back(7);v1.push_back(4);greater<int>gt;//定义一个函数对象在进行传参sort(v1.begin(), v1.end(),gt);for (auto& e : v1)cout << e << " ";cout << endl;sort(v1.begin(), v1.end(),less<int>());//直接调用匿名对象传参，进行排序for (auto& e : v1)cout << e << " ";//两个效果相同但是调用匿名对象更方便一点
}

 

5.测试代码 

void TestPriorityQueue()
{qyy::priority_queue<int,vector<int>,greater<int>> it;//用优先级队列创建变量it.push(1);//入队it.push(3);it.push(4);it.push(9);it.push(2);it.push(7);it.push(5);it.push(6);while (!it.empty())//队列不为空{cout << it.top()<<"  ";//获取堆顶元素it.pop();//出队//优先级队列pop数据的时候会将优先级高的数据先出队，它的pop和stack与queue的pop不同。}
}