NFA的确定化

一、实验目的

（1）通过本次实验，加深对正则表达式、NFA、DFA及其识别的语言的理解；
（2）掌握从NFA到DFA的转换，以及用子集法把NFA转换成DFA理论，编程实现将NFA（不确定有穷自动机）转换为DFA（确定有穷自动机）。

二、实验内容

将给定的NFA进行确定化，输出等价的DFA。要求选择合适的NFA的存储格式，并进行正确性检查。

三、实验原理

（1）NFA
NFA(nondeterministic finite-state automata)即非确定有限自动机, 一个非确定的有限自动机NFA M’是一个五元式：

NFA M’=(S, Σ∪{ε}, δ, S0, F)
其中 S—有限状态集
Σ∪{ε}—输入符号加上ε,即自动机的每个结点所射出的弧可以是Σ中一个字符或是ε。
S0—初态集 F—终态集
δ—转换函数 S×Σ∪{ε} →2S
(2S --S的幂集—S的子集构成的集合）

（2）DFA
DFA(deterministic finite-state automata)即确定有限自动机，一个确定的有限自动机DFA M是一个五元式:

M=(S, Σ，δ, S0, Z) 其中：
S —有限状态集
Σ—输入字母表
δ—映射函数(也称状态转换函数)
S×Σ→S
δ(s,a)=S’, S, S’ ∈S, a∈Σ
S0 —初始状态 S0 ∈S
Z—终止状态集 Z S

（3）NFA和DFA之间的联系
在非确定的有限自动机NFA中，由于某些状态的转移需从若干个可能的后续状态中进行选择，故一个NFA对符号串的识别就必然是一个试探的过程。这种不确定性给识别过程带来的反复，无疑会影响到FA的工作效率。而DFA则是确定的，将NFA转化为DFA将大大提高工作效率，因此将NFA转化为DFA是有其一定必要的。

四、实验结果

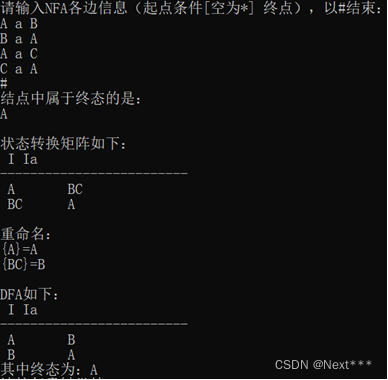
在这里插入图片描述

五、代码实现

#include<iostream>
#include<string>
#define MAXS 100
using namespace std;
string NODE;//结点集合
string CHANGE;//终结符集合
int N;//NFA边数
struct edge
{string first;string change;string last;
};
struct chan
{string ltab;string jihe[MAXS];
};
void kong(int a)
{int i;for (i = 0; i < a; i++)cout << ' ';
}
//排序
void paixu(string &a)
{int i, j;char b;for (j = 0; j < a.length(); j++) {for (i = 0; i < a.length(); i++) {if (NODE.find(a[i]) > NODE.find(a[i + 1])){b = a[i];a[i] = a[i + 1];a[i + 1] = b;}}}
}void eclouse(char c, string &he, edge b[])
{int k;for (k = 0; k < N; k++){if (c == b[k].first[0])if (b[k].change == "*"){if (he.find(b[k].last) > he.length())he += b[k].last;eclouse(b[k].last[0], he, b);}}
}void move(chan &he, int m, edge b[])
{int i, j, k, l;k = he.ltab.length();l = he.jihe[m].length();for (i = 0; i < k; i++)for (j = 0; j < N; j++)if ((CHANGE[m] == b[j].change[0]) && (he.ltab[i] == b[j].first[0]))if (he.jihe[m].find(b[j].last[0]) > he.jihe[m].length())he.jihe[m] += b[j].last[0];for (i = 0; i < l; i++)for (j = 0; j < N; j++)if ((CHANGE[m] == b[j].change[0]) && (he.jihe[m][i] == b[j].first[0]))if (he.jihe[m].find(b[j].last[0]) > he.jihe[m].length())he.jihe[m] += b[j].last[0];
}
//输出
void outputfa(int len, int h, chan *t)
{int i, j, m;cout << " I ";for (i = 0; i < len; i++)cout << 'I' << CHANGE[i] << " ";cout << endl << "-------------------------" << endl;for (i = 0; i < h; i++){cout << ' ' << t[i].ltab;m = t[i].ltab.length();for (j = 0; j < len; j++){kong(8 - m);m = t[i].jihe[j].length();cout << t[i].jihe[j];}cout << endl;}
}
int main()
{edge *b = new edge[MAXS];int i, j, k, m, n, h, x, y, len;bool flag;string jh[MAXS], endnode, ednode, sta;cout << "请输入NFA各边信息（起点条件[空为*] 终点），以#结束：" << endl;for (i = 0; i < MAXS; i++){cin >> b[i].first;if (b[i].first == "#")break;cin >> b[i].change >> b[i].last;}N = i;/*for(j=0;j<N;j++)cout<<b[j].first<<b[j].change<<b[j].last<<endl;*/for (i = 0; i < N; i++){if (NODE.find(b[i].first) > NODE.length())NODE += b[i].first;if (NODE.find(b[i].last) > NODE.length())NODE += b[i].last;if ((CHANGE.find(b[i].change) > CHANGE.length()) && (b[i].change != "*"))CHANGE += b[i].change;}len = CHANGE.length();cout << "结点中属于终态的是：" << endl;cin >> endnode;for (i = 0; i < endnode.length(); i++)if (NODE.find(endnode[i]) > NODE.length()){cout << "所输终态不在集合中，错误！" << endl;return 0;}//cout<<"endnode="<<endnode<<endl;chan *t = new chan[MAXS];t[0].ltab = b[0].first;h = 1;eclouse(b[0].first[0], t[0].ltab, b);//求e-clouse//cout<<t[0].ltab<<endl;for (i = 0; i < h; i++){for (j = 0; j < t[i].ltab.length(); j++)for (m = 0; m < len; m++)eclouse(t[i].ltab[j], t[i].jihe[m], b);//求e-clousefor (k = 0; k < len; k++){//cout<<t[i].jihe[k]<<"->";move(t[i], k, b);//求move(I,a)//cout<<t[i].jihe[k]<<endl;for (j = 0; j < t[i].jihe[k].length(); j++)eclouse(t[i].jihe[k][j], t[i].jihe[k], b);//求e-clouse}for (j = 0; j < len; j++){paixu(t[i].jihe[j]);//对集合排序以便比较for (k = 0; k < h; k++){flag = operator==(t[k].ltab, t[i].jihe[j]);if (flag)break;}if (!flag&&t[i].jihe[j].length())t[h++].ltab = t[i].jihe[j];}}cout << endl << "状态转换矩阵如下：" << endl;outputfa(len, h, t);//输出状态转换矩阵//状态重新命名string *d = new string[h];NODE.erase();cout << endl << "重命名：" << endl;for (i = 0; i < h; i++){sta = t[i].ltab;t[i].ltab.erase();t[i].ltab = 'A' + i;NODE += t[i].ltab;cout << '{' << sta << "}=" << t[i].ltab << endl;for (j = 0; j < endnode.length(); j++) {if (sta.find(endnode[j]) < sta.length())d[1] = ednode += t[i].ltab;}for (k = 0; k < h; k++) {for (m = 0; m < len; m++) {if (sta == t[k].jihe[m])t[k].jihe[m] = t[i].ltab;}}}for (i = 0; i < NODE.length(); i++) {if (ednode.find(NODE[i]) > ednode.length())d[0] += NODE[i];}endnode = ednode;cout << endl << "DFA如下：" << endl;outputfa(len, h, t);//输出DFAcout << "其中终态为：" << endnode << endl;//DFA最小化 system("pause");
}