MCMC(Markov Chain Monte Carlo)是一种经典的概率分布采样方法。本文对其概念和常见算法做简单梳理。
解决什么问题?
我们常常遇到这样的问题:模型构建好之后,有一个概率 p ( x ) p(x) p(x)(称为目标分布),不能显式的给出其表达,只能生成一系列符合这个分布的 x x x。这种问题称为“采样”。
特别地,在贝叶斯方法中,关注的是后验概率 p ( x ∣ D ) p(x|D) p(x∣D)。在给定观测 D D D的情况下,需要估计系统参数 x x x。如果后验概率没有明确表达,或者由于多重积分难以计算,则无法直接求解 x x x,但是可以生成一系列符合此概率的分布。
常见的情况是,后验概率难以明确表达。在已知观测数据x的情况下,利用 p ( x ∣ D ) = p ( x ) ⋅ p ( D ∣ x ) / p ( D ) ∝ p ( D ∣ x ) p(x|D) = p(x) \cdot p(D|x) / p(D) \propto p(D|x) p(x∣D)=p(x)⋅p(D∣x)/p(D)∝p(D∣x)。对似然函数进行采样。
名字解析
Monte Carlo方法:用多次随机求平均的方法来逼近一个值。实际是采样方法的核心。
举例:落球箱(模型)给定。可以通过累加每个针处的概率来计算最终的落球分布,也可以多次投球来逼近这个分布。
Markov Chain方法:用 x x x的转移概率逼近平稳概率。
构建一系列 x x x,后一个的取值通过前一个取值以及状态转移概率获得。Monte Carlo方法的每一个采样是独立的,而Markov Chain Monte Carlo的采样是前后关联的。
举例:已知 p ( 阴 转 晴 ) p(阴转晴) p(阴转晴)和 p ( 晴 转 阴 ) p(晴转阴) p(晴转阴),则可以构建MC链获得晴天和阴天的概率。
最初的一段MC链往往混合不够充分,不符合稳态分布,不能使用。这一阶段称为burn-in。
为了降低MC链采样的相关性,有些文献采用thinning的方法:每隔N个样本接受一个。
使用这种方法,往往需要另外设置一些隐变量来帮助构建状态转移关系。
举例:最简单的神经网络,由一个显结点和一个隐结点构成。已知 p ( h ∣ v ) , p ( v ∣ h ) p(h|v), p(v|h) p(h∣v),p(v∣h),可以构建MC链获得 p ( v ) p(v) p(v)。
设计MCMC方法的一个难处,在于如何设计合理的转移概率函数,使得MC链的稳态分布等于要求的概率分布。
MCMC的另一个问题是混合速度,在这篇博客中有所讨论。
MCMC是一个大类,有许多种具体算法,以下举例几种最为著名的。
Gibbs Sampling
Gibbs Sampling处理这样的问题:对于一个高维随机变量 x = [ x 1 , x 2 , x 3 ] \textbf{x}=[x^1,x^2,x^3] x=[x1,x2,x3],不能写出其各分量的联合概率 p ( x ) p(x) p(x),但是可以写出各个分量之间的条件概率。
首先任取初始值 x 0 \textbf{x}_0 x0。在已知当前采样 x t \textbf{x}_t xt时,按照如下方法生成t+1时刻采样。
- 根据 x 2 x^2 x2, x 3 x^3 x3采样 x 1 x^1 x1: x t + 1 1 ∝ p ( x 1 ∣ x t 2 , x t 3 ) x_{t+1}^1 \propto p(x^1|x^2_t, x^3_t) xt+11∝p(x1∣xt2,xt3)
- 根据 x 1 x^1 x1, x 3 x^3 x3采样 x 2 x^2 x2: x t + 1 2 ∝ p ( x 2 ∣ x t + 1 1 , x t 3 ) x_{t+1}^2 \propto p(x^2|x^1_{t+1}, x^3_t) xt+12∝p(x2∣xt+11,xt3)
- 根据 x 1 x^1 x1, x 2 x^2 x2采样 x 3 x^3 x3: x t + 1 3 ∝ p ( x 3 ∣ x t + 1 1 , x t + 1 2 ) x_{t+1}^3 \propto p(x^3|x^1_{t+1}, x^2_{t+1}) xt+13∝p(x3∣xt+11,xt+12)
每一次采样,都尽可能利用其他分量的最新结果。Gibbs Sampling特别适用于贝叶斯网络的采样,因为该网络本身就包含一系列条件概率。
Metropolis-Hastings(MH)
MH方法的一个优点是,即使不能写出概率密度函数 p ( x ) p(x) p(x),可以用一个和其成正比的函数 f ( x ) f(x) f(x)来采样。如前所述,这在贝叶斯方法中非常方便。
首先任取初始值 x 0 x_0 x0。在已知当前采样 x t x_t xt时,按照如下方法生成t+1时刻采样。
- 根据一个概率分布 Q ( x t + 1 ∣ x t ) Q(x_{t+1}|x_t) Q(xt+1∣xt)生成一个候选采样 x t + 1 x_{t+1} xt+1。
其中 Q Q Q称为proposal density或者jumping distribution。可以取以 x t x_t xt为中心的高斯分布。 - 比较新旧采样的概率密度函数
如果 f ( x t + 1 ) > f ( x t ) f(x_{t+1})>f(x_t) f(xt+1)>f(xt),接受 x t + 1 x_{t+1} xt+1为新采样;
否则,按照 p = f ( x t + 1 ) / f ( x t ) p=f(x_{t+1})/f(x_t) p=f(xt+1)/f(xt)选择 x t + 1 x_{t+1} xt+1为新采样,或者维持 x t x_t xt为新采样。
一种常见的情况,如果待求概率是一个后验 p ( x ∣ D ) p(x|D) p(x∣D),且其先验是高斯,则可以做如下变换:
p ( x ∣ D ) ∝ p ( x ) ⋅ p ( D ∣ x ) = N ( x ; 0 , Σ ) ⋅ p ( D ∣ x ) p(x|D) \propto p(x)\cdot p(D|x) = N(x; 0, \Sigma) \cdot p(D|x) p(x∣D)∝p(x)⋅p(D∣x)=N(x;0,Σ)⋅p(D∣x)
直接使用以下方法生成候选样本
x t + 1 = 1 − ϵ 2 x t + ϵ ν x_{t+1} = \sqrt{1-\epsilon^2}x_t + \epsilon \nu xt+1=1−ϵ2xt+ϵν
其中 ν ∼ N ( 0 , Σ ) \nu \sim N(0,\Sigma) ν∼N(0,Σ), ϵ ∈ [ − 1 , + 1 ] \epsilon\in[-1,+1] ϵ∈[−1,+1]是扰动步长。新样本等于当前样本和先验的加权和。另一种表达方法是
x t + 1 = cos θ ⋅ x t + sin θ ⋅ ν x_{t+1} = \cos{\theta} \cdot x_t + \sin{\theta} \cdot \nu xt+1=cosθ⋅xt+sinθ⋅ν
不同的 ϵ \epsilon ϵ对应的新采样的轨迹是半个椭圆圆周。椭圆的两轴分别为 x t x_t xt和 ν \nu ν。如果 ϵ = 0 \epsilon=0 ϵ=0,则新采样和旧采样相同(红色)。 ϵ 或 者 θ \epsilon或者\theta ϵ或者θ控制扰动幅度。
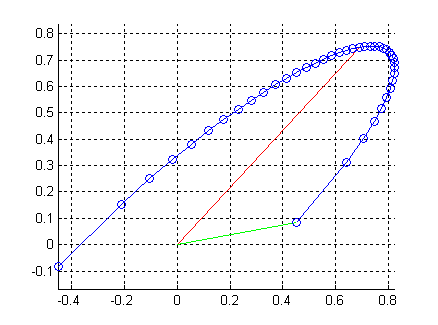
对于某些高斯过程分类器,MH方法比Gibbs Sampling快。且实现简单。缺点是 Q Q Q的参数(例如叠加的高斯的方差,或者 ϵ \epsilon ϵ)
需要手工调整。
Slice Sampling
Slice Sampling方法利用一种几何思路:根据概率密度函数曲线高度来采样,越高的地方slice越宽,采样越多。同样可以对和概率密度函数成正比的任一函数 f ( x ) f(x) f(x)来进行采样。
首先任取初始值 x 0 x_0 x0。在已知当前采样 x t x_t xt时,按照如下方法生成t+1时刻采样。
- 在 [ 0 , f ( x t ) ] [0, f(x_t)] [0,f(xt)]之间均匀采样,得到 y y y
- 过 y y y做一条平行于 x x x轴的直线,在其位于 y = f ( x ) y=f(x) y=f(x)曲线内部的范围内(slice),均匀采样得到 x t + 1 x_{t+1} xt+1
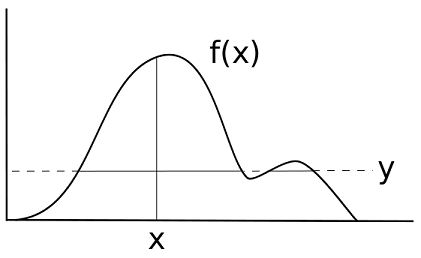
曲线越高,截取的横线越宽,x采样的概率越大。
在求曲线内部线段时,需要求 x = f − 1 ( y ) x=f^{-1}(y) x=f−1(y)。如果 f f f的反函数不好求,可能需要用一维采样方法找出 x x x。
Slice Sampling的一个优点是:不需要手工调整参数。
Elliptical Slice Sampling
此方法是Slice Sampling的进化版本,不需要求 f f f的反函数;同时结合了Metropolis-Hastings方法中在椭圆上采样的思想,但不再需要人工设定 θ \theta θ。
此方法要求目标概率为一后验概率,其先验为高斯,似然函数用 L L L表示。
p ( x ∣ D ) ∝ p ( x ) ⋅ p ( D ∣ x ) = N ( x ; 0 , Σ ) ⋅ L ( x ) p(x|D) \propto p(x)\cdot p(D|x) = N(x; 0, \Sigma) \cdot L(x) p(x∣D)∝p(x)⋅p(D∣x)=N(x;0,Σ)⋅L(x)
首先任取初始值 x 0 x_0 x0。在已知当前采样 x t x_t xt时,按照如下方法生成t+1时刻采样。
- 按照先验随机生成 ν ∼ N ( 0 , Σ ) \nu \sim N(0,\Sigma) ν∼N(0,Σ)。 ν \nu ν和 x t x_t xt的组合构成一个椭圆。
- 随机生成一个比原来似然函数略低的门限
t h r e s h = log p ( D ∣ x ) + log u , 其 中 u ∼ U [ 0 , 1 ] thresh = \log {p(D|x)} + \log u, 其中u\sim U[0,1] thresh=logp(D∣x)+logu,其中u∼U[0,1] - 随机生成一个 θ ∼ U [ 0 , 2 π ] \theta \sim U[0,2\pi] θ∼U[0,2π],设定 θ \theta θ的初始搜索范围
θ m i n = θ − 2 π , θ m a x = θ \theta_{min} = \theta - 2\pi, \theta_{max} = \theta θmin=θ−2π,θmax=θ - 生成候选新采样 x t + 1 = x t c o s θ + ν s i n θ x_{t+1} = x_t cos\theta+\nu sin\theta xt+1=xtcosθ+νsinθ
- 如果候选新采样比门限好, log L ( x t + 1 ) > t h r e s h \log L(x_{t+1}) > thresh logL(xt+1)>thresh,接受 x t + 1 x_{t+1} xt+1。返回。
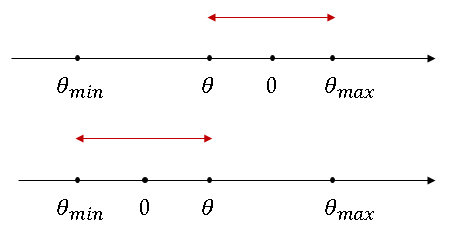
- 否则,缩小 θ \theta θ的搜索范围
如 果 θ < 0 , θ m i n = θ ; 否 则 θ m a x = θ 如果\theta<0, \theta_{min} = \theta; 否则\theta_{max} = \theta 如果θ<0,θmin=θ;否则θmax=θ - 重新采样 θ ∼ U [ θ m i n , θ m a x ] \theta \sim U[\theta_{min}, \theta_{max}] θ∼U[θmin,θmax],返回步骤4。
在步骤6,7中, θ \theta θ的范围逐渐围绕着0缩小。新生成的候选采样逐渐接近于上一个采样 x t x_t xt,步骤4中的条件越来越容易满足。