一、题目描述

输入两个整数 n 和 m ，输出一个 n 行 m 列的矩阵，将数字 1 到 n × m 按照回字蛇形填充至矩阵中。

具体矩阵形式可参考样例。

输入格式：

输入共一行，包含两个整数 n 和 m 。

输出格式：

输出满足要求的矩阵。

矩阵占 n 行，每行包含 m 个空格隔开的整数。

数据范围：

1 ≤ n, m ≤ 100

输入样例：

3 3

输出样例：

1 2 3
8 9 4
7 6 5

二、思路讲解

蛇形矩阵，就是将数字以 回字形 填充到 二维数组 中，比如这样：

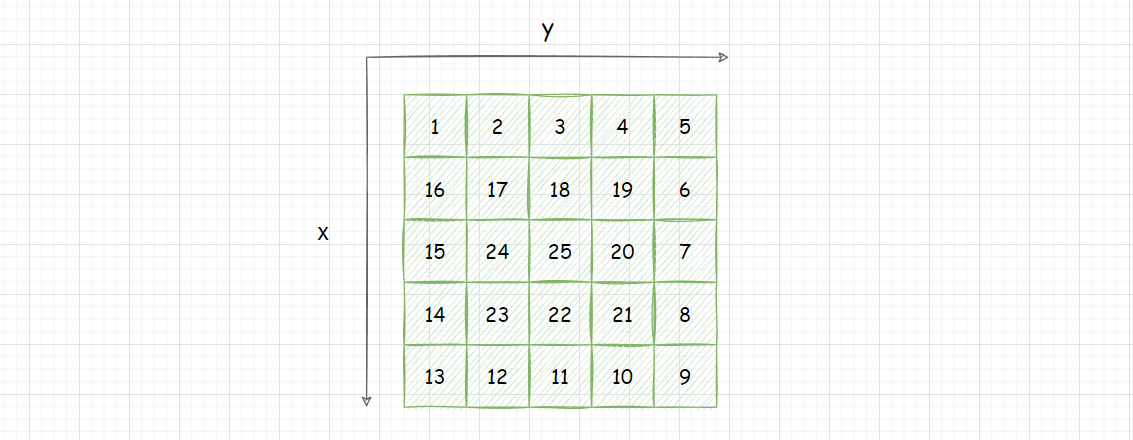
我们把 二维数组的行 看做 x轴，二维数组的列 看做 y轴。

结合数轴，我们其实可以发现蛇形矩阵填数的规律：从左上角第一个元素开始，先向右填，碰边；向下填，碰边；向左填，碰边；向上填，碰到已经填过的位置，退回原位；向右填 … 之后就是重复上面的规律来填充。

通过规律可以发现 蛇形矩阵 填数的其实是和 x, y 两个轴是息息相关的，我们将数据的坐标记为 (x, y)：

向右走：(x, y) --> (x, y + 1)，纵坐标 + 1
向下走：(x, y) --> (x + 1, y)，横坐标 + 1
向左走：(x, y) --> (x, y - 1)，纵坐标 - 1
向上走：(x, y) --> (x - 1, y)，横坐标 - 1

而上面四种移动在 题目中的具体表现 就像下面这样：

x 不动 - x = 0，y 向右移 - y + 1
y 不动 - y = 0，x 向下移 - x + 1
x 不动 - x = 0，y 向左移 - y - 1
y 不动 - y = 0，x 向上移 - x - 1

所以 x 和 y 的坐标变化就分别有 4 种。便可以把这些移动方式存入数组：dx[] = { 0, 1, 0, -1 }, dy[] = { 1, 0, -1, 0 }。

从开始填数到填数完成需要改变很多次方向，那么什么情况需要改变填数方式？

填数越过左边界
填数越过右边界
填数越过上边界
填数越过下边界
填数位置已有数据

第五点 是最需要注意的，其实后面大多都是第五种情况，前四种情况基本只会在 最外一圈 用到。

在里层 碰到填过的数据 就得 “回退并拐弯” ，以免覆盖填过的数据。

到这儿主题思路其实已经讲完了，下面再讲一下细节：

如果坐标 x 或 y “飙错位置” ，如何把它 “拉回正确位置” ？可以用 a ，b 变量分别记录当前坐标在移动后是否超出范围，重新调整 移动方法 ，实际上就是重新选取 dx 或 dy 数组中 合适的元素 ，然后重新计算 a 和 b ，将坐标 拉回来 ，做出正确调整，再将 a 和 b 赋给 x 和 y 。

下面我们看看代码怎么写。

三、代码实现

#include <iostream>using namespace std;const int N = 110;// 全局中定义数组，元素默认初始化为0
int q[N][N];int n, m;int main()
{cin >> n >> m;int dx[] = { 0, 1, 0, -1 }, dy[] = { 1, 0, -1, 0 };// 起始 x 和 y 在 (0, 0)，并且 d 为 0，对应着 x 不动，y 往右走int x = 0, y = 0, d = 0;for (int i = 1; i <= n * m; i++){q[x][y] = i;// 计算 a, b 的下一个位置int a = x + dx[d], b = y + dy[d];// 判断是否超限// 这里 q[a][b] 其实有一层妙用，由于全局数组是被初始化 0 的，// 只要填过数，q[a][b] 就必定为真if (a < 0 || a >= n || b < 0 || b >= m || q[a][b]){// 移动到下一个位置，% 4 获取 [0, 3] 下标d = (d + 1) % 4;a = x + dx[d], b = y + dy[d];}// 将正确的 a b 赋给 x yx = a, y = b;}for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){cout << q[i][j] << " ";}cout << endl;}return 0;
}