前言

一维线性函数，也称为一次函数，是指只有一个自变量 $x$ 的函数，且函数表达式可以写成 $y = a x + b$ 的形式，其中 $a$ 和 $b$ 是常数。具体来说， $a$ 称为斜率，决定了函数图像的倾斜程度； $b$ 称为截距，决定了函数图像与 $y$ 轴的交点位置。
优化一维线性函数的目标是找到一个使得函数值最小或最大的 $x$ 值。

粒子群算法（Particle Swarm Optimization，PSO）是一种启发式优化算法，它源于对鸟群捕食行为的研究。在粒子群算法中，被优化的问题被视为一个多维空间中的目标函数，算法通过模拟群体中每个粒子在空间中的搜索行为来寻找目标函数的全局最优解。

每个粒子在搜索空间中的位置表示一个潜在解，其速度表示了搜索方向和步长。每个粒子具有一个适应度值，该适应度值根据目标函数的表现来计算。粒子群算法通过协同粒子的行为来优化目标函数。粒子的速度和位置在每个迭代中被更新，使其朝着群体中的最佳位置和全局最佳位置移动。

粒子群算法的运行过程如下：

初始化粒子群，包括每个粒子的初始位置和速度，并设置全局最佳位置和全局最佳适应度值为初始值。
计算每个粒子的适应度值，更新全局最佳位置和全局最佳适应度值。
更新每个粒子的速度和位置，根据每个粒子当前位置与全局最佳位置之间的差异来调整速度和位置。
重复步骤2和3，直到达到指定的停止准则，如达到最大迭代次数或满足收敛要求。

在实践中，粒子群算法经常与其他优化算法结合使用，例如遗传算法、模拟退火等。这些算法的组合可以提高搜索效率和准确性，从而提高优化问题的解决效率。

正文

粒子群算法可以用来优化一维线性函数。具体地，我们可以将一维线性函数 $f (x)$ 转化为目标函数 $y (x)$ ，使得 $y (x)$ 的取值范围为[0, 1]，且函数值越小表示越优，函数值越大表示越差。具体转化方式如下：

$\frac{f(x) - \min f(x)}{\max f(x) - \min f(x)}$

其中 $max⁡f(x)\max f(x)$ 和 $min⁡f(x)\min f(x)$ 分别是函数 $f (x)$ 在一定区间内的最大值和最小值。这样，优化 $f (x)$ 就可以转化为优化 $y (x)$ ，即找到使得 $y (x)$ 最小的 $x$ 值。

在粒子群算法中，我们可以初始化一些粒子，并在每一次迭代中更新粒子的速度和位置，直到达到一定的停止条件。在更新速度和位置时，我们需要使用上文提到的公式，同时需要指定一些超参数，例如学习因子、惯性权重、加速度权重等。具体可以参考之前的回答。

在优化一维线性函数时，粒子群算法可以在一定的迭代次数内找到一个相对较优的解。但是需要注意，对于线性函数，我们也可以通过解析求导的方式直接求得最优解，因此粒子群算法在实际中并不常用于优化线性函数。

函数实现

%%
clear
close all
warning off
clc
%%
% 调用粒子群算法求解
x_min = -10;
x_max = 10;
n_pop = 50;
n_iter = 100;
w = 0.8;
c1 = 1.5;
c2 = 1.5;
[gbest, gbest_val] = pso(@objfun, x_min, x_max, n_pop, n_iter, w, c1, c2);% 输出结果
fprintf('最优解：x = %f，最优值：%f\n', gbest, gbest_val);% 目标函数
function y = objfun(x)y = 2*(x-3).^2 + 10;
end% 粒子群算法
function [gbest, gbest_val] = pso(objfun, x_min, x_max, n_pop, n_iter, w, c1, c2)% 参数设置x_range = x_max - x_min;v_min = -x_range;v_max = x_range;% 初始化粒子pop = x_min + rand(n_pop, 1) * x_range;v = v_min + rand(n_pop, 1) * (v_max - v_min);pbest = pop;pbest_val = objfun(pop);[gbest_val, gbest_idx] = min(pbest_val);gbest = pbest(gbest_idx);% 迭代for i = 1:n_iter% 更新速度和位置r1 = rand(n_pop, 1);r2 = rand(n_pop, 1);v = w*v + c1*r1.*(pbest-pop) + c2*r2.*(gbest-pop);pop = pop + v;% 边界处理pop(pop < x_min) = x_min;pop(pop > x_max) = x_max;% 更新个体历史最优和全局历史最优pbest_val_new = objfun(pop);pbest_update_idx = pbest_val_new < pbest_val;pbest(pbest_update_idx) = pop(pbest_update_idx);pbest_val(pbest_update_idx) = pbest_val_new(pbest_update_idx);[gbest_val_new, gbest_idx_new] = min(pbest_val);if gbest_val_new < gbest_valgbest = pbest(gbest_idx_new);gbest_val = gbest_val_new;endend
end

通过改变 $x$ 的范围 $x_min = -10;x_max = 10;$ 来得到一维线性函数的最优值

可视化处理

%%
clear
close all
warning off
clc
%%
% 调用粒子群算法求解
x_min = -10;
x_max = 10;
n_pop = 50;
n_iter = 100;
w = 0.8;
c1 = 1.5;
c2 = 1.5;
[gbest, gbest_val] = pso(@objfun, x_min, x_max, n_pop, n_iter, w, c1, c2);% 输出结果
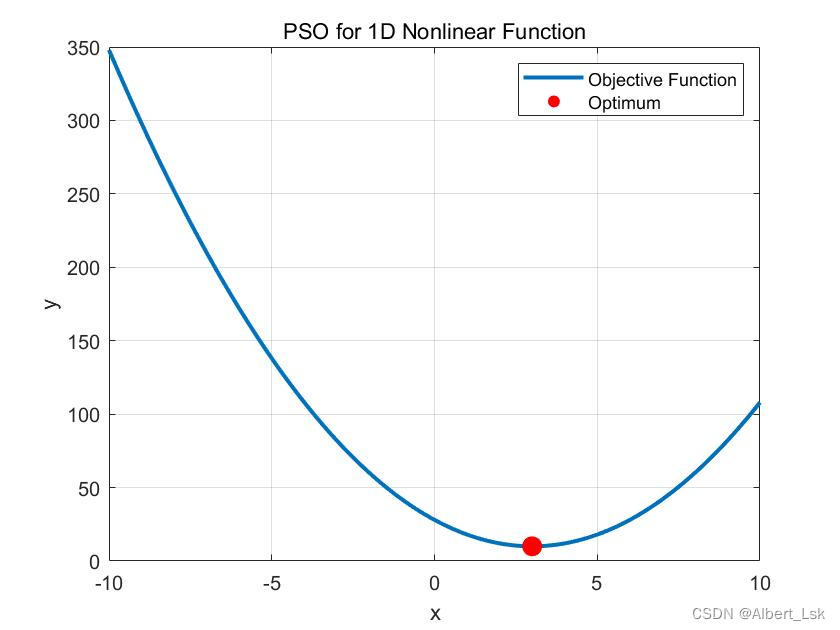
fprintf('最优解：x = %f，最优值：%f\n', gbest, gbest_val);% 可视化处理
x = linspace(x_min, x_max, 1000);
y = objfun(x);
figure();
plot(x, y, 'linewidth', 2);
hold on;
scatter(gbest, gbest_val, 100, 'r', 'filled');
xlabel('x');
ylabel('y');
title('PSO for 1D Nonlinear Function');
legend('Objective Function', 'Optimum');
grid on;% 目标函数
function y = objfun(x)y = 2*(x-3).^2 + 10;
end% 粒子群算法
function [gbest, gbest_val] = pso(objfun, x_min, x_max, n_pop, n_iter, w, c1, c2)% 参数设置x_range = x_max - x_min;v_min = -x_range;v_max = x_range;% 初始化粒子pop = x_min + rand(n_pop, 1) * x_range;v = v_min + rand(n_pop, 1) * (v_max - v_min);pbest = pop;pbest_val = objfun(pop);[gbest_val, gbest_idx] = min(pbest_val);gbest = pbest(gbest_idx);% 迭代for i = 1:n_iter% 更新速度和位置r1 = rand(n_pop, 1);r2 = rand(n_pop, 1);v = w*v + c1*r1.*(pbest-pop) + c2*r2.*(gbest-pop);pop = pop + v;% 边界处理pop(pop < x_min) = x_min;pop(pop > x_max) = x_max;% 更新个体历史最优和全局历史最优pbest_val_new = objfun(pop);pbest_update_idx = pbest_val_new < pbest_val;pbest(pbest_update_idx) = pop(pbest_update_idx);pbest_val(pbest_update_idx) = pbest_val_new(pbest_update_idx);[gbest_val_new, gbest_idx_new] = min(pbest_val);if gbest_val_new < gbest_valgbest = pbest(gbest_idx_new);gbest_val = gbest_val_new;endend
end