绪论

信号相关

信号:信息的载体
电信号源的电路表达形式
$$i_{\mathrm{s}}=\frac{v_{\mathrm{s}}}{R_{\mathrm{s}}}$$


注意:实际应用中,避免不必要的转换,传感器转换为电压时,就视为电压源

信号的频谱
正弦信号
$v(t)=V_{\mathrm{m}}\sin \left({\omega }_{0}t+\theta \right)$
$T=\frac{2\pi }{{\omega }_0}{\omega }_0=2\pi f_0$

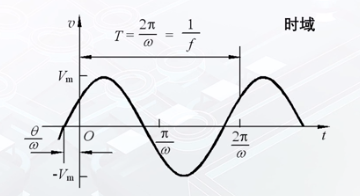
对其进行傅里叶变换

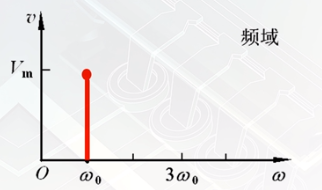
方波信号

周期函数满足狄利克雷条件， 可展开成傅里叶级数。
$$v(t)=\frac{V_{\mathrm{s}}}{2}+\frac{2V_{\mathrm{s}}}{\pi }\left(\sin {\omega }_{0}t+\frac{1}{3}\sin 3{\omega }_{0}t+\frac{1}{5}\sin 5{\omega }_{0}t+\cdots \right)$$
$\begin{array}{rl}& {\omega }_0=\frac{2\pi }{T}⟶\text{ 基波角频率 }\\ & \frac{V_{\mathrm{s}}}{2}⟶\text{ 直流分量 }\end{array}$
$\begin{array}{rl}& \sin {\omega }_{0}t是基波\\ & \sin 3{\omega }_{0}t是三次谐波\\ & \sin 5{\omega }_0是五次谐波t\end{array}$
$\frac{2V_{\mathrm{s}}}{\pi }⟶基波分量$

$\frac{2V_{\mathrm{s}}}{\pi }\cdot \frac{1}{3}⟶三次谐波分量$

$\frac{2V_{\mathrm{s}}}{\pi }\cdot \frac{1}{5}⟶五次谐波分量$

次数越高,对原来波形的影响越小

傅里叶级数的标准形式
$v(t)=\frac{V_{\mathrm{s}}}{2}+\frac{2V_{\mathrm{s}}}{\pi }\sum _{n=1,3,5,\cdots }^{\infty }\frac{1}{n}\cos \left(n{\omega }_{0}t-\frac{\pi }{2}\right)$

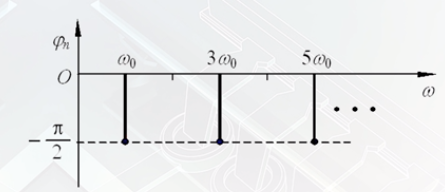
频谱:信号的幅值和相位随频率变化的分布，称为该信号的频谱
主要讨论幅度谱，或幅频响应

方波可以看成是基波和谐波的叠加，叠加的越多，就越接近方波的时域表示。

$$v(t)=\frac{V_{\mathrm{s}}}{2}+\frac{2V_{\mathrm{s}}}{\pi }\left(\sin {\omega }_{0}t+\frac{1}{3}\sin 3{\omega }_{0}t+\frac{1}{5}\sin 5{\omega }_{0}t+\cdots \right)$$
常数项使得表达式无论如何＞0
非周期信号的频域表示

非周期信号随着频率的增加，频谱函数的总趋势总是衰减

非周期信号
傅里叶变换：
周期信号 一一离散频率函数
非周期信号 一一 连续频率函数
周期性⇌离散
非周期信号包含了所有可能的 频兹成分（0 ≤ω<∞)
快速傅里叶变换（FFT）+计算机
→可求山非周期信号的频谱函数

模拟信号：时间和幅值上都是连续的信号
数字信号：时间和幅值上都是离散的信号

.	模拟信号	数字信号
信号状态	连续	0,1
器件工作	放大区	饱和区或截止区
研究对象	电路输入与输出的电压电流关系	电路输入与输出的逻辑关系

处理模拟信号的电子电路称为模拟电路
最基本的处理：对信号的放大

放大电路模型抽象

放大器

音频放大器



A：Amplification，放大倍数；v：Voltage；o：Output；i：Input；i：Imax； r：Resistance；g：
电压增压
$A_v=\frac{v_o}{v_i}$
电流增益
$A_i=\frac{i_o}{i_i}$
互阻增益（互阻放大电路）
$A_r=\frac{v_o}{i_i}（\Omega ）$
互导增益
$A_g=\frac{i_o}{v_i}（S）$

$A_{\mathrm{v}\mathrm{o}}⟶$负载开路时的电压增益
$R_{\mathrm{i}}⟶$ 输入电阻
$R_{\mathrm{o}}⟶$ 输出电阻

放大电路模型分析

电压放大电路

由输出回路得
$v_{\mathrm{o}}=A_{vo}{v}_{\mathrm{i}}\frac{R_{\mathrm{L}}}{R_{\mathrm{o}}+R_{\mathrm{L}}}$
则电压增益为
$A_v=\frac{v_0}{v_{\mathrm{i}}}=A_{v0}\frac{R_{\mathrm{L}}}{R_{\mathrm{o}}+R_{\mathrm{L}}}$
由此可见
$R_{\mathrm{L}}\downarrow ⟶A_v\downarrow$
即负载的大小会影响增益的大小
$A_v=\frac{v_0}{v_i}=A_{vo}\frac{1}{1+R_o/R_L}$
要想减少负载的影响
${\mathbf{R}}_{\mathrm{o}}<<{\mathbf{R}}_{\mathrm{L}}$ 理想情况 $R_{\mathrm{o}}=0$

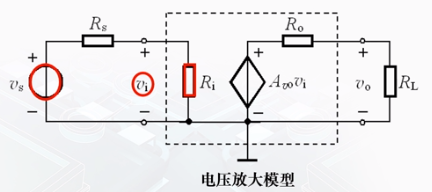
$v_{\mathrm{i}}=\frac{R_{\mathrm{i}}}{R_{\mathrm{s}}+R_{\mathrm{i}}}{v}_{\mathrm{s}}{R}_{\mathrm{i}}>>R_{\mathrm{s}}$
理想情况 $R_i=\infty$
电压放大电路适用于：$R_S$较小且$R_L$较大的场合

电流放大模型

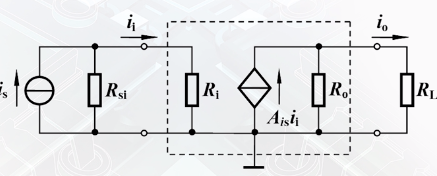
关心输出电流与输入电流的关系
$A_{is}$表示当输出端短路的时候所对应的放大倍数,即负载短路时的电流增益
曲输出回路得

$i_{\mathrm{o}}=A_{\mathrm{i}\mathrm{s}}{i}_{\mathrm{i}}\frac{R_{\mathrm{o}}}{R_{\mathrm{o}}+R_{\mathrm{L}}}$

则电流增益为
$A_i=\frac{i_o}{i_{\mathrm{i}}}=A_{is}\frac{R_o}{R_{\mathrm{o}}+R_{\mathrm{L}}}$

由此可见
$R_{\mathrm{L}}\uparrow ⟶A_i\downarrow$
若要减少负载影响
$R_0>>R_{\mathrm{L}}$ 理想情况${\mathbf{R}}_{\mathrm{o}}=\infty$

由输入回路得 $i_i=i_s\frac{R_{\mathrm{s}}}{R_{\mathrm{s}}+R_{\mathrm{i}}}$
若要减少对信号源的衰减
$R_{\mathrm{i}}<<R_{\mathrm{s}}$ 理想情况 $R_{\mathrm{i}}=0$
互阻放大模型,互导放大模型,利用戴维南诺顿等效变换原理,可以互相变换

电流放大电路适用于：$R_S$较大且$R_L$较小的场合

主要性能指标

增益Av,输入电阻Ri,输出电阻Ro

放大器的性能指标是衡量器件品质优劣的标准， 决定了它的使用范围。
输入电阻
$R_{\mathrm{i}}=\frac{v_{\mathrm{i}}}{i_{\mathrm{i}}}$
决定了放大电路从信号源吸取信号的能力
求解的时候,需要将实际信号源拿掉,加入一个测试电压
定量分析：
$R_{\mathrm{i}}=\frac{v_{\mathrm{t}}}{i_{\mathrm{i}}}$

输出电阻
${\mathbf{R}}_{\mathrm{o}}={\frac{v_{\mathrm{t}}}{{\mathbf{i}}_{\mathrm{t}}}|}_{}{v}_{\mathrm{s}}=0,R_{\mathrm{L}}=\infty$
输出电阻大小决定了放大电路带负载能力
带负载能力:放大电路输出量随负载变化的程度(增量与变化前数值的比,百分比越小,带负载能力越强)

增益
反映放大电路在输入信号控制下，将供电电源能量转换为输出信号能量的能力。
四种增益
$A_v=\frac{v_0}{v_i}{A}_i=\frac{i_0}{i_i}{A}_r=\frac{v_0}{i_i}{A}_g=\frac{i_0}{v_i}$

$电压增益=20\lg \mid A_v(dB)$
$电流增益=20\lg \mid A_i(dB)$
$电流增益=10\lg A_P(dB)$
2倍的关系是因为功率与电压电流是平方关系
$10\lg \frac{p_0}{p_i}=10\lg \frac{v_0^2/R}{v_i^2/R}=10\lg \frac{v_0^2}{v_i^2}=20\lg \frac{v_0^2}{v_i^2}$
对数表示法的好处
极大的扩大了视野范围
简化运算,乘法变加法(多级放大电路的增益)

频率响应和非线性失真

在输入正弦信号情况下，输出随输入
信号频率连续变化的稳态响应，称为放大
电路的频率响应。

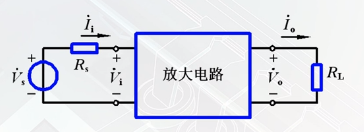
电压增益可表示为
${\dot{A}}_v(\mathrm{j}\omega )=\frac{{\dot{V}}_0(\mathrm{j}\omega )}{{\dot{V}}_1(\mathrm{j}\omega )}$
$=\left|\frac{{\dot{V}}_0(j\omega )}{{\dot{V}}_1(j\omega )}\right|\angle {\phi }_0(\omega )-{\phi }_i(\omega )]$
或写为 ${\dot{\mathbf{A}}}_v={\mathbf{A}}_v(\omega )\angle \phi (\omega )$

$A_v(\omega )=\left|\frac{{\dot{V}}_0(j\omega )}{{\dot{V}}_1(j\omega )}\right|$ 称为幅频响应
$\phi (\omega )={\phi }_{\mathrm{o}}(\omega )-{\phi }_{\mathrm{i}}(\omega )$ 称为相频响应

波特图
纵轴:dB
横轴:指数坐标
中频带也叫通频带
其中 $f_{\mathrm{H}}-$ 上限频率 $f_{\mathrm{L}}$ 一一下限频率
$BW=f_{\mathrm{H}}-f_{\mathrm{L}}$
称为带宽(bandwidth)

两种频率失真:幅度失真和相位失真,都是线性失真(电感电容对每一个频率的放大倍数是不变的)
幅度失真:
对不同频率的信号增益不同产生的失真。
产生失真的原因：
放大电路的带宽是有限的，不可能对信号的所有频率都进行同样的放大。

相位失真
对不同频率的信号相移产生的失真
相移:输出的正弦波和输入的正弦波信号的相位差称为相移

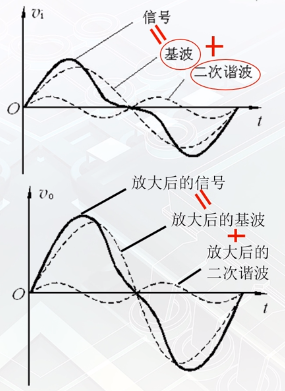
非线性失真

由元器件非线性特性引起的失真

左边对某一频率分量，$A_v=\frac{v_0}{v_{\mathrm{i}}}$ 为常数,右边则是变化的

方法
将曲线表示为多项式之和
$y=a_o+a_{1}x+a_2{x}^2+\cdots$
$v_o=a_o+a_1\sin \omega t+a_2{\sin }^2\omega t+\cdots$
输出波形产生高次谐波分量

非线性失真系数:
$\gamma =\frac{\sqrt{\sum _{k=2}^{\infty }{V}_{ok}^2}}{V_{o1}}\times 100\%$

$V_{\mathrm{o}1}$是输出电压信号基波分量的有效值,
$V_{\mathrm{o}k}$ 是输出电压信号基波分量的有效值，k为正整数。

其他指标：
最大输出功率、转换速率、信噪比、抗干扰能力等。
体积、重量、工作温度、环境温度等。
达到性能指标：合理设计电路+高质量的元器件+高水平的制造工艺

书中有关符号的约定
大写字母、大写下标表示直流量。如，$V_{CE},I_C$等
小写字母、大写下标表示总量(含交流直流)。如，$V_{CE},i_B$等
小写字母、小写下标表示纯直流量。如,$V_{cc},i_b等$

问题总结

题型

输出电压,输出电阻

某放大电路在负载开路时，测得输出电压为5V，在输入电压不变的情况下接入3KΩ的负载电阻，输出电压下降到3V，说明该放大电路的输出电阻为（）KΩ。
某放大电路在接有2KΩ负载电阻时，测得输出电压为3V，在输入电压不变的情况下断开负载电阻，输出电压上升到7.5V，说明该放大电路的输出电阻为（）KΩ。
已知某放大电路的输出电阻为3KΩ，在接有4KΩ负载电阻时，测得输出电压为2V。在输入电压不变的条件，断开负载电阻，输出电压将上升到（）V。
$$\begin{gathered} V_i,R_i不变,因此I_i不变,以第二问为例 \\ \frac{3}{2}+\frac{3}{R_0}=\frac{7.5}{R_0} \end{gathered}$$

当接入1KΩ的负载电阻 $R_L$时，电压放大电路的输出电压比负载开路时的输出电压下降了 20%， 求该放大电路的输出电阻。
解: $R_o=\left(\frac{v_o}{\frac{5}{4}{v}_o}-1\right)R_L=\left(\frac{5}{4}-1\right)R_L=\frac{1}{4}{R}_L=\frac{1}{4}(1K\Omega )=250\Omega$
$\frac{R_L}{(RO+RL)}=0.8$

放大倍数

测得某放大电路的输入正弦电压和电流的峰值分别为10mV和10μA，在负载电阻为2KΩ时，测得输出正弦电压信号的峰值为2V。试计算该放大电路的电压放大倍数 电流放大倍数和功率放大倍数。
${\dot{\mathrm{A}}}_{\mathrm{v}}=\frac{{\dot{V}}_o}{{\dot{V}}_i}=\frac{2\mathrm{V}}{10\mathrm{m}\mathrm{V}}=\frac{2000\mathrm{m}\mathrm{V}}{10\mathrm{m}\mathrm{V}}=200$
${\dot{\mathrm{A}}}_{\mathrm{i}}=\frac{{\dot{I}}_o}{{\dot{I}}_i}=\frac{\frac{{\dot{V}}_o}{R_L}}{{\dot{I}}_i}=\frac{\frac{2000}{2000}}{10\mu \mathrm{A}}=\frac{1\mathrm{m}\mathrm{A}}{10\mu \mathrm{A}}=100$
${\mathrm{A}}_{\mathrm{p}}=\frac{P_o}{P_i}=\frac{V_o\cdot I_o}{V_i\cdot I_i}=\frac{2\mathrm{V}\cdot \mathrm{lm}\mathrm{A}}{10\mathrm{m}\mathrm{V}\cdot 10\mu 0}=2\times 10^4$
${\mathrm{A}}_{\mathrm{u}}=20\lg \frac{V_o}{V_i}=20\lg 200=20\lg 2+20\lg 100=20\times 0.7+40=54\mathrm{d}\mathrm{B}$
${\mathrm{A}}_{\mathrm{i}}=20\lg \frac{{\dot{I}}_o}{{\dot{I}}_i}=20\lg 100=20\lg 10^2=40\mathrm{d}\mathrm{B}$
${\mathrm{A}}_{\mathrm{p}}=10\lg \frac{P_o}{P_i}=10\lg \left(2\times 10^4\right)=10\lg 2+10\lg 10^4=7+40=47\mathrm{d}\mathrm{B}$

课程无关

电阻R是resistance，为什么电导G找不到对应单词