文章目录
- 树
- 二叉树
- 二叉树的性质
- 完全二叉树
- 二叉树的存储
- 遍历二叉树和线索二叉树
- 6.4 树和森林
- 哈夫曼树
- 应用
树
-
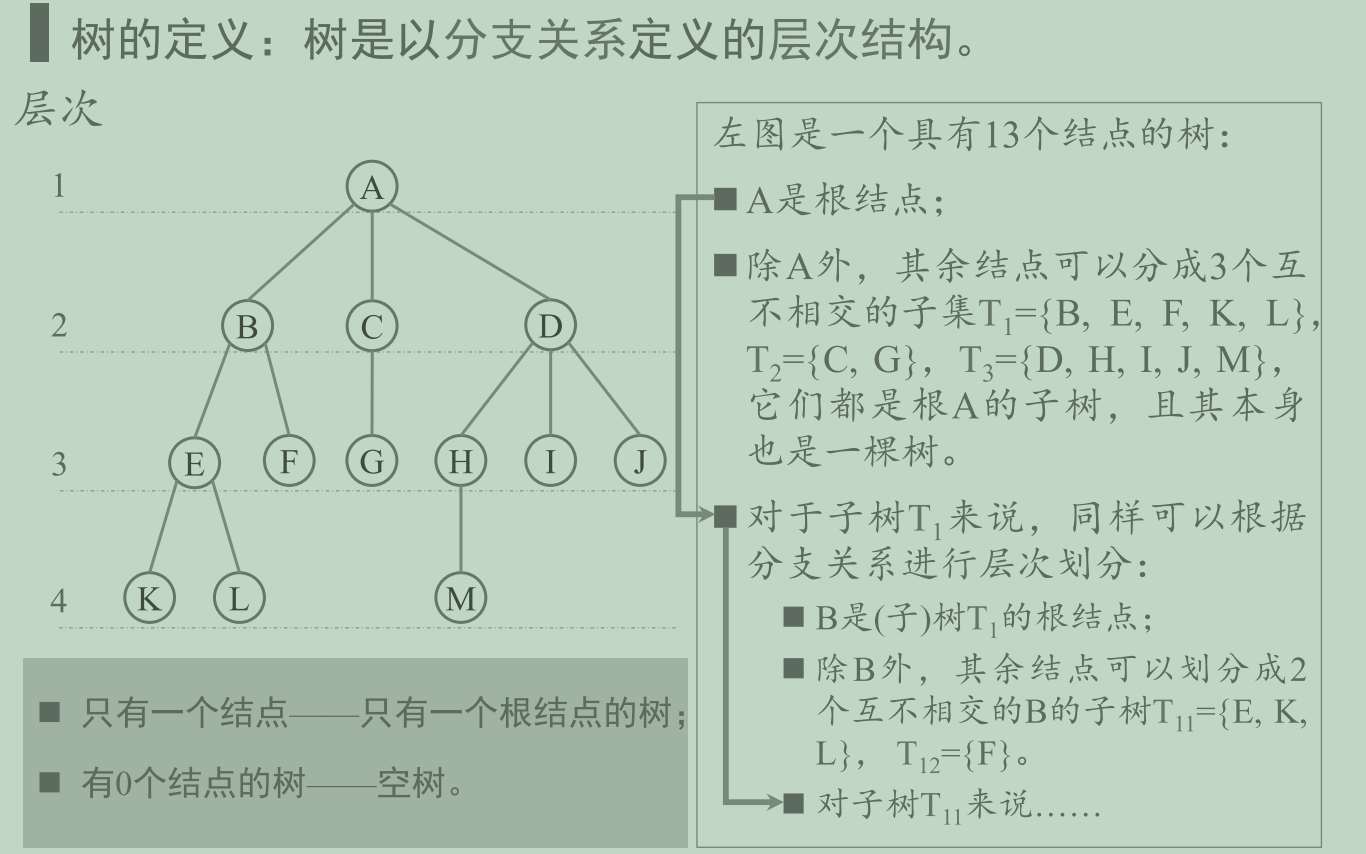
树的定义:树是以分支关系定义的层次结构。
-
D; 树(Tree)是n(n≥0)个结点的有限集。
-
R 数据关系
有且仅有一个特定的称为根(Root) 的结点
当n>1时,除根以外的其余结点 可分为m(m>0)个互不相交的有限 集T1, T2 ,… ,Tm ,其中每一个集 合本身又是一棵树,并且称为根 的子树(SubTree)。
-
只有一个结点——只有一个根结点的树;
-
有0个结点的树——空树
-
分支结点: 非终端结点
-
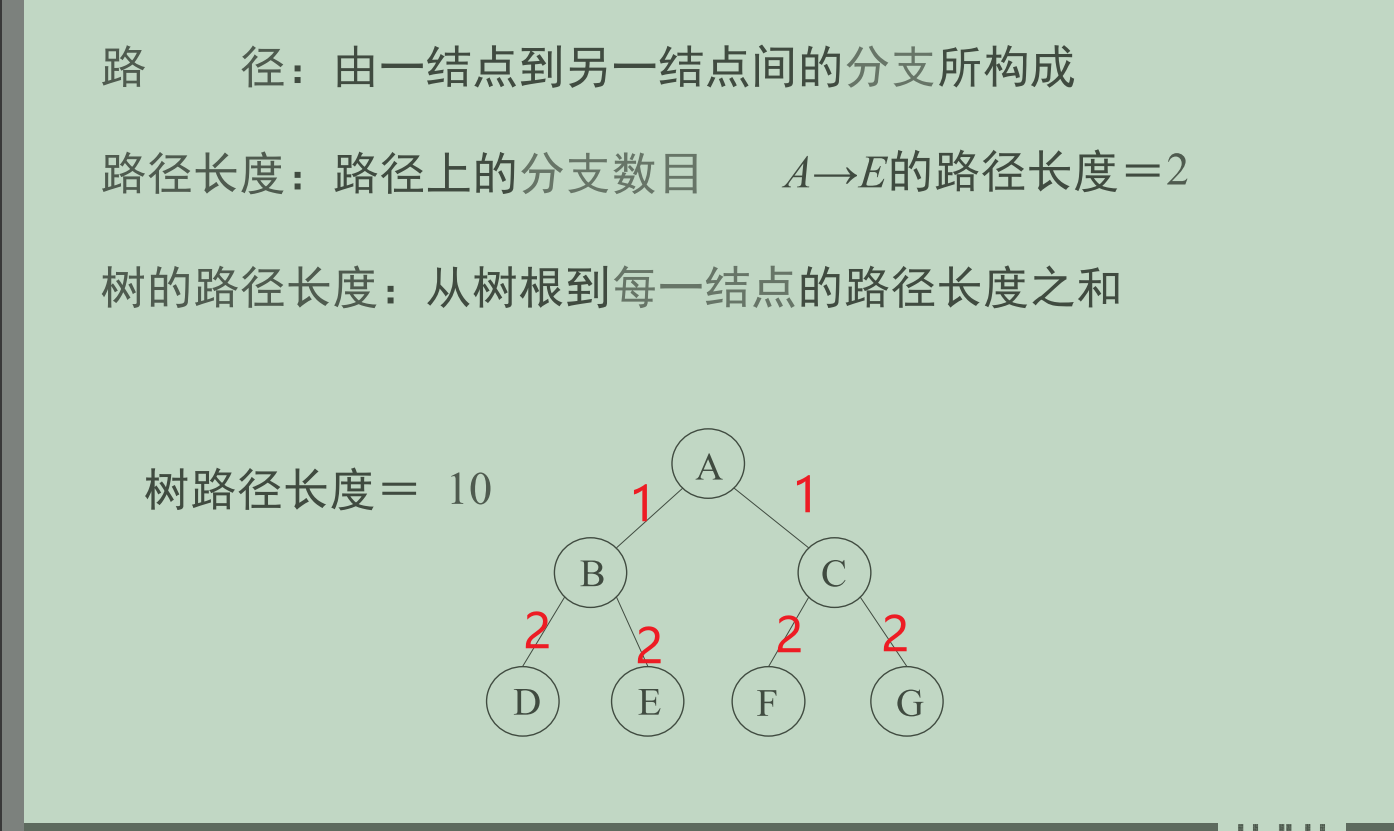
结点层次指的是结点在树中所处的层次;
-
堂兄弟指的是具有相同父亲的兄弟结点;
-
树的深度指的是树中所有结点中最大层数;
-
有序树指的是树中每个结点的子节点之间具有顺序关系;无序树则相反,子节点之间没有顺序关系;
-
森林则指由若干棵互不相交的树组成。
-
孩子指的是一个结点的直接后代;
-
双亲指的是一个结点的直接前驱;
-
兄弟指的是具有相同双亲的结点;
-
祖先指的是从根到某一结点路径上所有结点;
-
子孙则指某一结点为根的子树中所有结点。
-
叶子结点指的是度为0的结点;
-
分支结点指的是度不为0的结点;
-
内部结点指的是除根节点和叶子节点以外的所有节点;
-
树的度指的是树中所有结点中最大度数。
二叉树
二叉树(Binary Tree) 是另一种树形结构 特点是每个结点最多只有两棵子树(即二 叉树中不存在度>2的结点) 二叉树的子树有左右之分,其次序不能 任意颠倒
二叉树的性质
-
性质1 在二叉树的第i层上至多有2i-1个结点(i≥1)
-
性质2 深度为k的二叉树至多有
2k-1个结点(k≥1) -
性质3 对任一棵二叉树T,如果其终端结点数为n0,度为2的 结点数为n2,则n0=n2+1
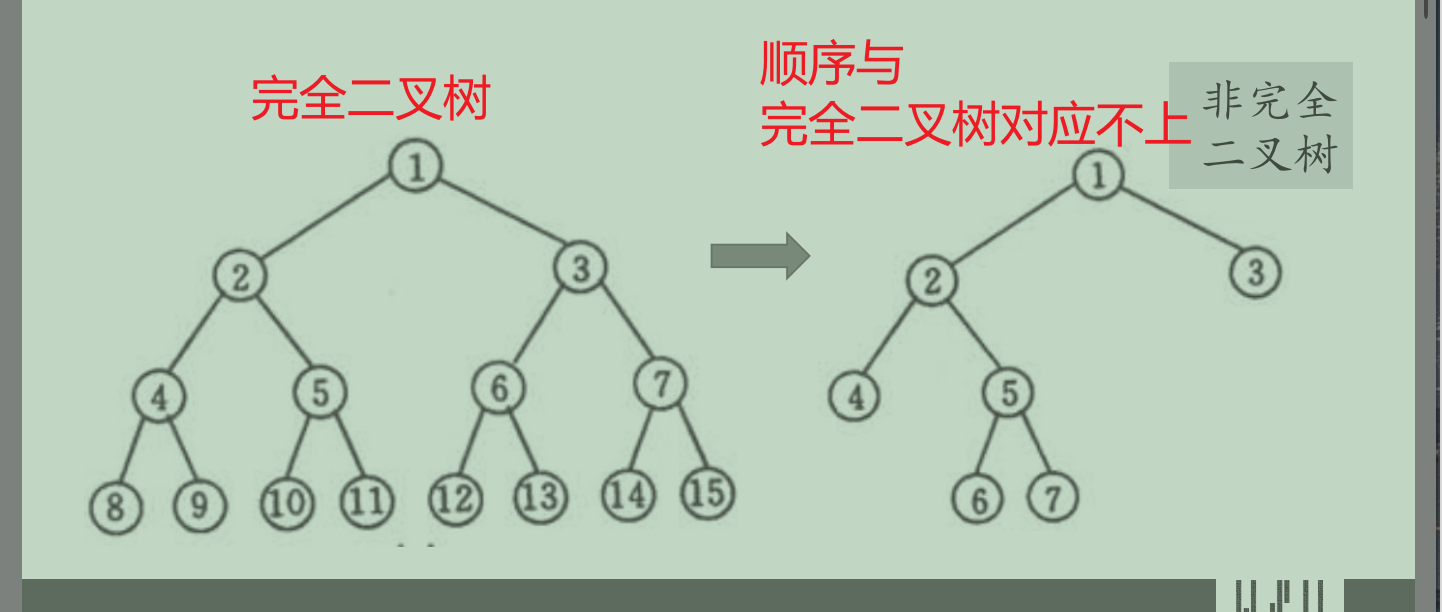
完全二叉树
- 满二叉树 一棵深度为k且有2k-1个结点的二叉树
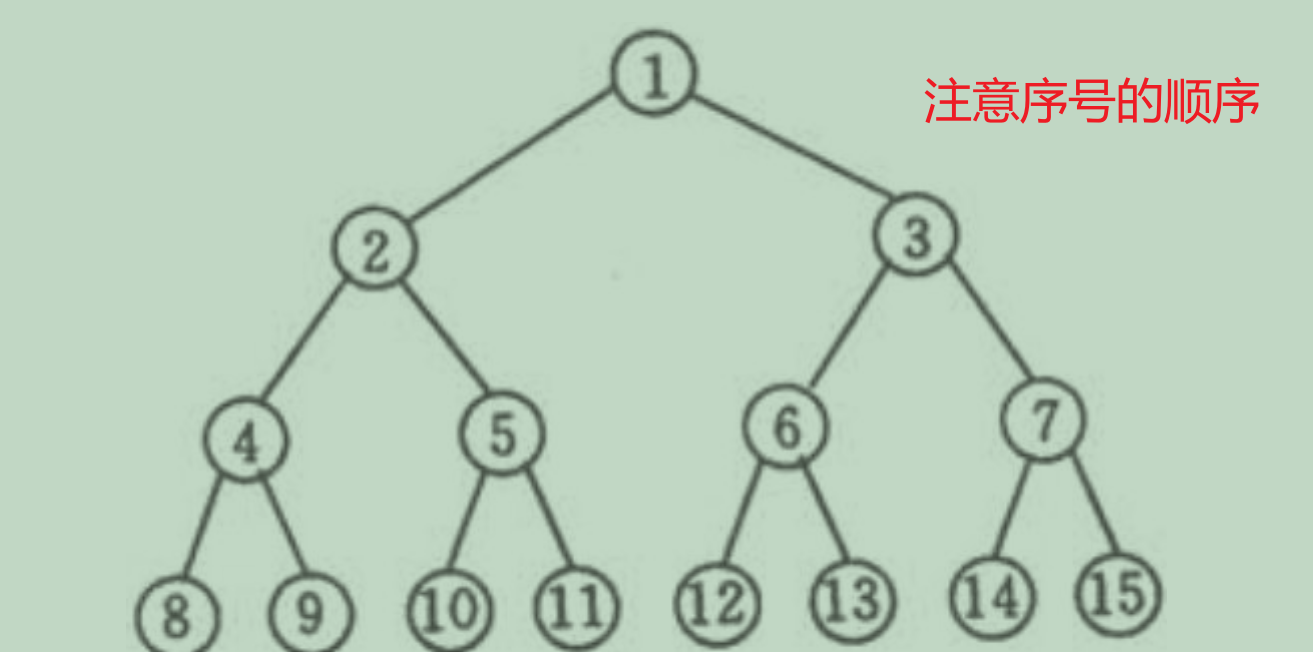
- 深度为k,有n个结点的二叉树,当且仅当其每一个 结点都与深度为k的满二叉树中编号从1至n的结点 一一对应时
某一结点 有右子树, 则其必有 左子树 - 叶子结点只可能在层次最大的两层上出现
- 对任一结点,若其右分支的子孙最大层次为l,则其 左下分支的子孙的最大层次必为l或l+1
-
性质4 具有n个结点的完全二叉树的深度为 log2 n + 1
-

二叉树的存储
- 顺序存储结构
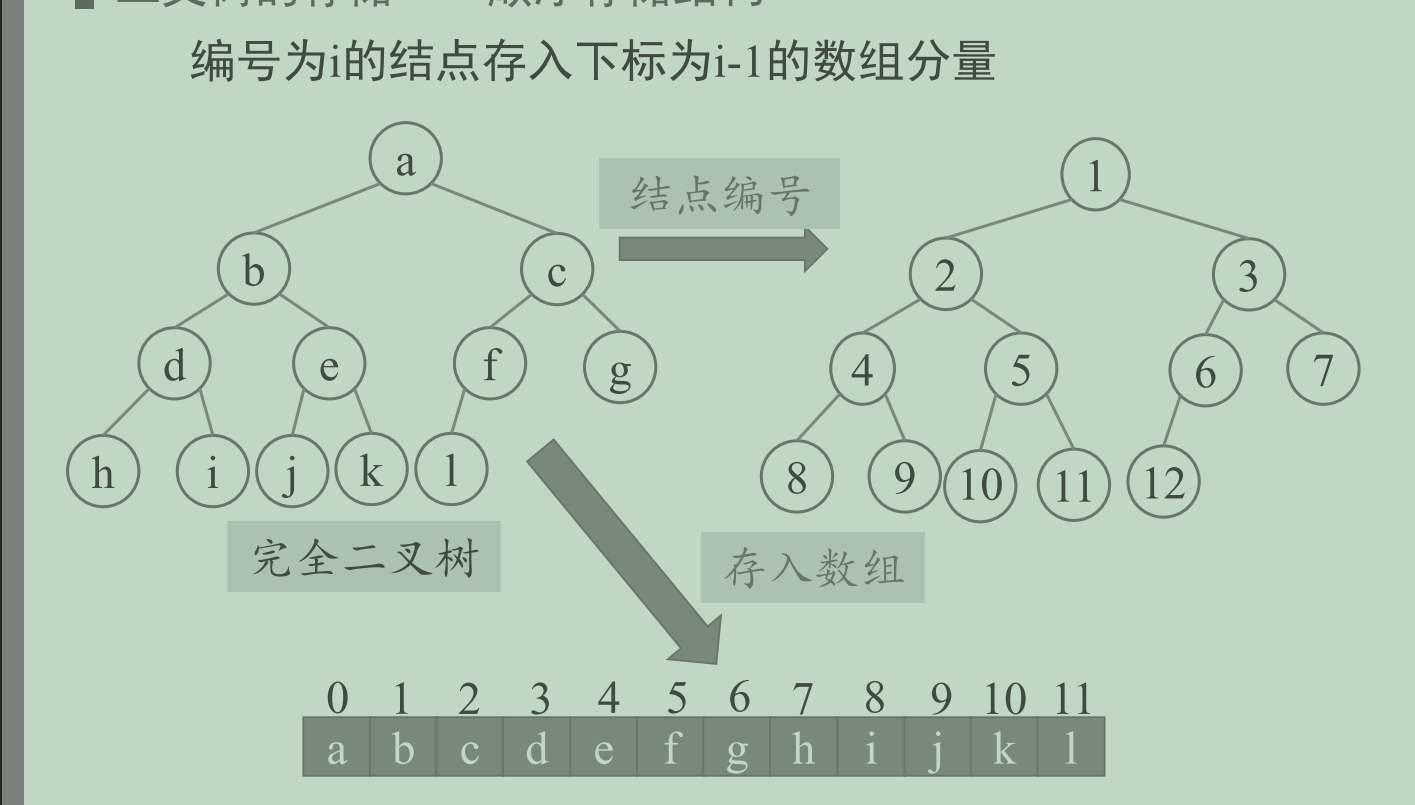
- 链式存储结构
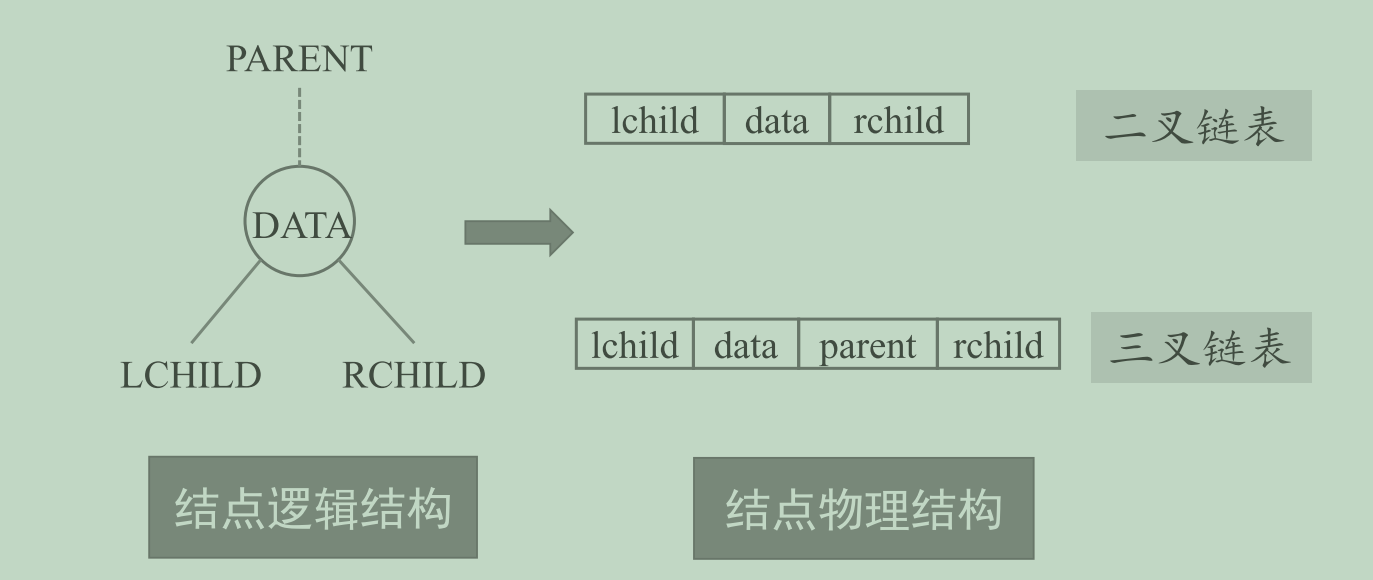
- 知识点 在含有n个结点的二叉链表中有n+1个空链域

遍历二叉树和线索二叉树
- 对线性结构而言,顺序遍历;
- 二叉树是非线性结构,每个结点有两个后继,则存在如 何遍历,即按什么样的搜索路径遍历的问题。

- 看ppt 有代码实现
二叉树遍历的时间效率和空间效率
基本操作:访问结点Visit()
- 时间效率:O(n) //每个结点只访问一次
- 空间效率:O(n) //栈占用的最大辅助空 间
6.4 树和森林
-
树的存储结构——双亲表示法
-
利用每个结点只有一个 双亲的性质
-
采用多重链表,即每个结点设置多个指针域,每个指针域指 向一棵子树的根结点

-
树林遍历顺序 和 树一样 ( 顺序即为第几棵树的Root结点)
-
树的存储结构——孩子兄弟表示法 / 二叉树表示法 / 二叉链 表表示法
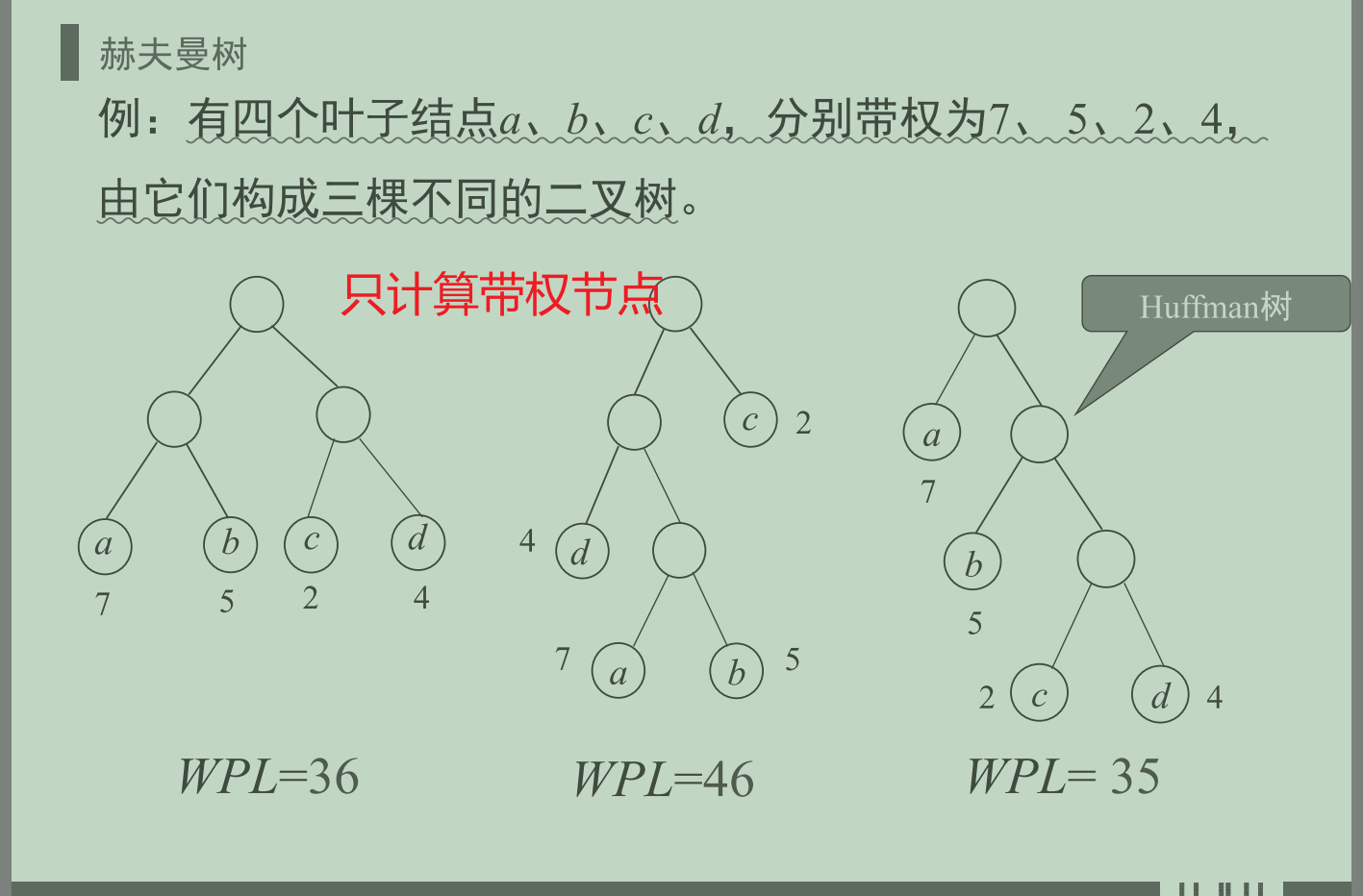
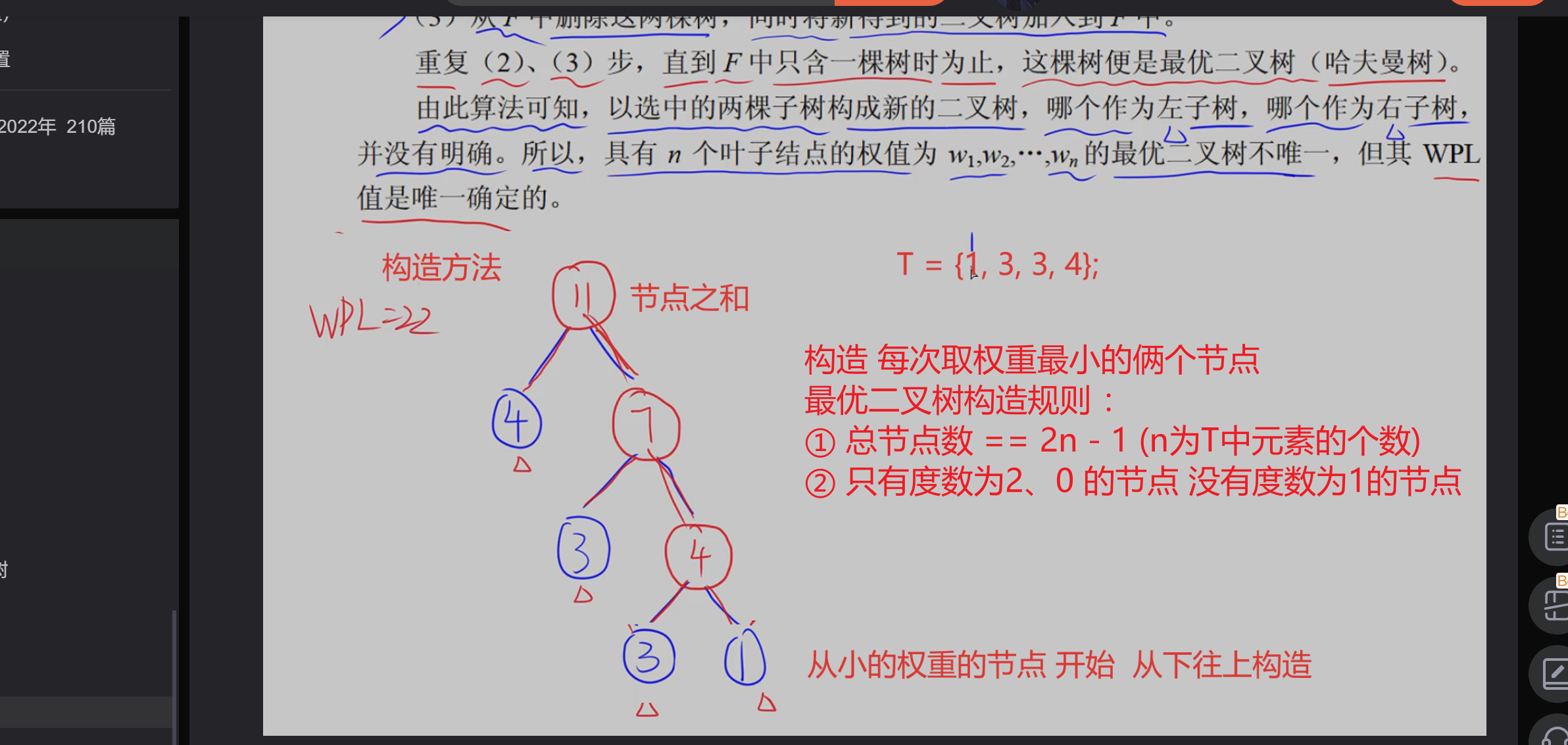
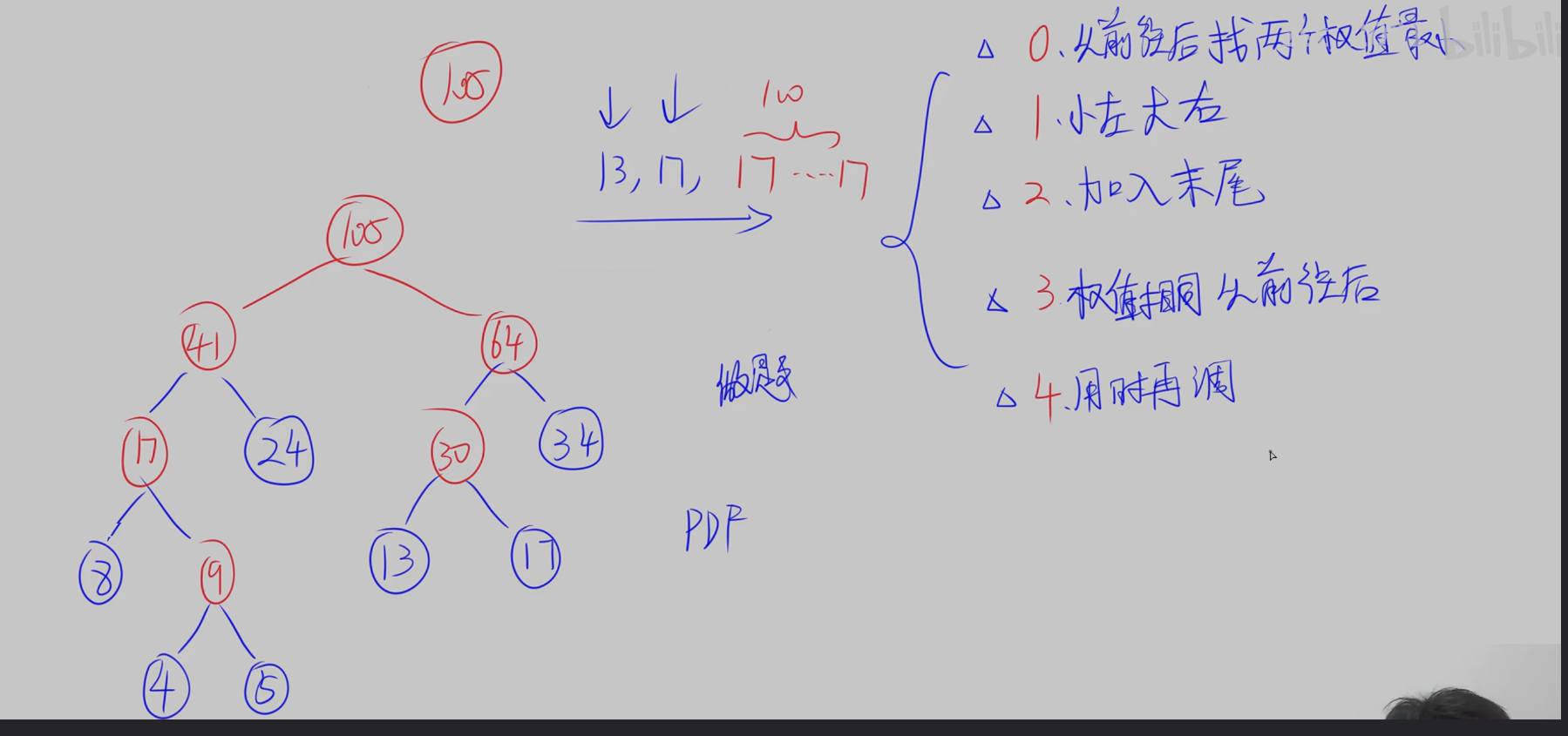
哈夫曼树

应用
1)二进制编码 : 通信中,可以采用0、1的不同排列来表示不同的字符, 称为二进制编码。 发送端需要将电文中的字符序列转换成二进制的0、1 序列,即编码; 接受端需要把接受的0、1序列转换成对应的字符序列, 即译码。 (左0 右 1)
2} 前缀编码 : 若对某一字符集进行不等长编码,则要求字符集中任一字符的编码都不能是其他字符编码的前缀。符合此要求的编码叫 做前缀编码


![[手撕数据结构]栈的深入学习-java实现](https://img-blog.csdnimg.cn/bec4322e33dd46e78ca00edfb2654de6.png)