最近在研究图像增强处理过程中,阅读了关于全局拉普拉斯平滑(global laplacian smoothing),加权最小二乘平滑(weighted least squares --wls)等技术文章,深感此类方法的精妙,并且这种优化思想可以用在许多地方:例如纹理去除,这也是本篇需要重点讲的paper:Structure Extraction from Texture via Relative Total Variation; 图像融合 ,对应文章为:《Poisson Image Editing》;图像降噪,对应文章为:《Edge-Preserving Decompositions for Multi-Scale Tone and Detail Manipulation》。
上面链接为项目主页地址,利用此类思想的图像处理文章不止上述方向,后面有时间会针对上面几篇paper总结说明,开始本篇paper:《Strucutre extraction from texture via relative total variation》的总结,关于这篇文章的说明网上也找到挺多,有些我借用说明,加上自己的一些理解。
文章介绍
很多自然场景和人工艺术品都包含纹理,见下图,它们有一个共同的特征就是:图像中有意义的结构图和纹理融合在一起,可以称这类图片为“结构+纹理”图片。在不去除纹理的前提下,人可以理解这些图像,其中图像的结构信息是人类视觉感知的主要数据,而不是纹理。文章的目的是提取出图像中有意义的结构。
方法介绍:
文章提出了一种基于总变差模型,该模型可以将图像中的结构和纹理区分开,模型如下:
I为输入图像,p为2D图像像素的索引,S表示要输出的结构图像,下三角表示一阶差分运算,其中第二项可以分为x方向和y方向两个方向上的形式:
作者的目的是提取各种不同类型的结构,所以并不针对某种特定类型的纹理结构图像,为了求解上面的模型,作者进行了下面的转换形式:
其中:
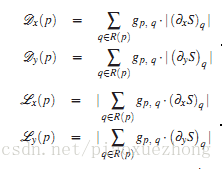
q是以p点为中心的一个方形区域内所有像素点的索引,其中g为高斯函数:
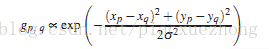
其中图(a)是一幅包含纹理的图像。(b)看出纹理和结构像素点都会产生比较大的差分值,对应像素点的亮度比邻域高;(c)可以看出结构信息对应的值大于纹理值,一种直觉上的解释为:在一个局部小窗口中,主要结构往往比复杂纹理具有更多相似方向的梯度。
因为自己并没有去复现文章的求解过程,具体求解过程参加文章,这里紧要复述一下:
上述公式的第二行是一个近似计算,结果是二次项
上式中

上面是针对X方向,Y方向同样的道理。
数学求解时,公式(3)可以转换成如下矩阵形式:
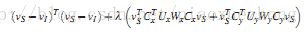
其中vs和vi是S和I的两个列向量,Cx和Cy是向前差分算子,
此时可以通过求矩阵的逆运算,或者用预处理共轭梯度法等求解。原文的代码是公开的,如下所示:
function S = tsmooth(I,lambda,sigma,sharpness,maxIter) if (~exist('lambda','var')) lambda=0.01; end if (~exist('sigma','var')) sigma=3.0; end if (~exist('sharpness','var')) sharpness = 0.02; end if (~exist('maxIter','var')) maxIter=4; end I = im2double(I); x = I; sigma_iter = sigma; lambda = lambda/2.0; dec=2.0; for iter = 1:maxIter [wx, wy] = computeTextureWeights(x, sigma_iter, sharpness); x = solveLinearEquation(I, wx, wy, lambda); sigma_iter = sigma_iter/dec; if sigma_iter < 0.5 sigma_iter = 0.5; end end S = x;
end function [retx, rety] = computeTextureWeights(fin, sigma,sharpness) fx = diff(fin,1,2); fx = padarray(fx, [0 1 0], 'post'); fy = diff(fin,1,1); fy = padarray(fy, [1 0 0], 'post'); vareps_s = sharpness; vareps = 0.001; wto = max(sum(sqrt(fx.^2+fy.^2),3)/size(fin,3),vareps_s).^(-1); fbin = lpfilter(fin, sigma); gfx = diff(fbin,1,2); gfx = padarray(gfx, [0 1], 'post'); gfy = diff(fbin,1,1); gfy = padarray(gfy, [1 0], 'post'); wtbx = max(sum(abs(gfx),3)/size(fin,3),vareps).^(-1); wtby = max(sum(abs(gfy),3)/size(fin,3),vareps).^(-1); retx = wtbx.*wto; rety = wtby.*wto; retx(:,end) = 0; rety(end,:) = 0; end function ret = conv2_sep(im, sigma) ksize = bitor(round(5*sigma),1); g = fspecial('gaussian', [1,ksize], sigma); ret = conv2(im,g,'same'); ret = conv2(ret,g','same');
end function FBImg = lpfilter(FImg, sigma) FBImg = FImg; for ic = 1:size(FBImg,3) FBImg(:,:,ic) = conv2_sep(FImg(:,:,ic), sigma); end
end function OUT = solveLinearEquation(IN, wx, wy, lambda) [r,c,ch] = size(IN); k = r*c; dx = -lambda*wx(:); dy = -lambda*wy(:); B(:,1) = dx; B(:,2) = dy; d = [-r,-1]; A = spdiags(B,d,k,k); e = dx; w = padarray(dx, r, 'pre'); w = w(1:end-r); s = dy; n = padarray(dy, 1, 'pre'); n = n(1:end-1); D = 1-(e+w+s+n); A = A + A' + spdiags(D, 0, k, k); if exist('ichol','builtin') L = ichol(A,struct('michol','on')); OUT = IN; for ii=1:ch tin = IN(:,:,ii); [tout, flag] = pcg(A, tin(:),0.1,100, L, L'); OUT(:,:,ii) = reshape(tout, r, c); end else OUT = IN; for ii=1:ch tin = IN(:,:,ii); tout = A\tin(:); OUT(:,:,ii) = reshape(tout, r, c); end end
end 上面的代码使用matlab实现的,其中求解线性方程时涉及到了稀疏矩阵的方程求解,所以如果要使用c++实现,可能要借助eigen或armadillo等数学库工具,这篇博客对全变分模型进行了解释,并给出了c++实现,但是并没有使用稀疏矩阵求解,所以在处理较大尺寸的图像时,可能会存在内存过大问题,不过可以作为参考。其代码如下:
void CImageObj::Total_Variation(int iter, double dt, double epsilon, double lambda)
{ int i, j; int nx = m_width, ny = m_height; double ep2 = epsilon * epsilon; double** I_t = NewDoubleMatrix(nx, ny); double** I_tmp = NewDoubleMatrix(nx, ny); for (i = 0; i < ny; i++) for (j = 0; j < nx; j++) I_t[i][j] = I_tmp[i][j] = (double)m_imgData[i][j]; for (int t = 0; t < iter; t++) { for (i = 0; i < ny; i++) { for (j = 0; j < nx; j++) { int iUp = i - 1, iDown = i + 1; int jLeft = j - 1, jRight = j + 1; // 边界处理 if (0 == i) iUp = i; if (ny - 1 == i) iDown = i; if (0 == j) jLeft = j; if (nx - 1 == j) jRight = j; double tmp_x = (I_t[i][jRight] - I_t[i][jLeft]) / 2.0; double tmp_y = (I_t[iDown][j] - I_t[iUp][j]) / 2.0; double tmp_xx = I_t[i][jRight] + I_t[i][jLeft] - 2 * I_t[i][j]; double tmp_yy = I_t[iDown][j] + I_t[iUp][j] - 2 * I_t[i][j]; double tmp_xy = (I_t[iDown][jRight] + I_t[iUp][jLeft] - I_t[iUp][jRight] - I_t[iDown][jLeft]) / 4.0; double tmp_num = tmp_yy * (tmp_x * tmp_x + ep2) + tmp_xx * (tmp_y * tmp_y + ep2) - 2 * tmp_x * tmp_y * tmp_xy; double tmp_den = pow(tmp_x * tmp_x + tmp_y * tmp_y + ep2, 1.5); I_tmp[i][j] += dt*(tmp_num / tmp_den + lambda*(m_imgData[i][j] - I_t[i][j])); } } // 一次迭代 for (i = 0; i < ny; i++) for (j = 0; j < nx; j++) { I_t[i][j] = I_tmp[i][j]; } } // 迭代结束 // 给图像赋值 for (i = 0; i < ny; i++) for (j = 0; j < nx; j++) { double tmp = I_t[i][j]; tmp = max(0, min(tmp, 255)); m_imgData[i][j] = (unsigned char)tmp; } DeleteDoubleMatrix(I_t, nx, ny); DeleteDoubleMatrix(I_tmp, nx, ny);
}
Eigen::SparseMatrix<double> spdiags(const MatrixXd& B,const Eigen::Matrix<int, 1, 1>& d, int m, int n)
{Eigen::SparseMatrix<double> A(m, n);std::vector<Triplet < double >> triplets;for (int k = 0; k < d.size(); k++){int i_min = std::max(0, -d(k));int i_max = std::min(m - 1, n - d(k) - 1);int B_idx_start = m >= n ? d(k) : 0;for (int i = i_min; i <= i_max; i++){if (d(k)>0)triplets.emplace_back(i, i+d(k), B(B_idx_start + i, k));elsetriplets.emplace_back(i, i-i_min, B(B_idx_start + i, k));}}A.setFromTriplets(triplets.begin(), triplets.end());return A;
}
int main()
{//---------------------------------------Matrix<int, 1, 1> d1;MatrixXd d0(5,1);d0(0, 0) = 10; d0(1, 0) = 20;d0(2, 0) = 30; d0(3, 0) = 40;d0(4, 0) = 50;d1(0)=0;Eigen::SparseMatrix<double> Diag= spdiags(d02, d1, 5, 5);std::cout << Diag<< std::endl;
}
参考:
https://wenku.baidu.com/view/9caf94767375a417866f8ff1.html
http://blog.sina.com.cn/s/blog_4bdb170b0101ovi8.html
https://www.cnblogs.com/Imageshop/p/3365517.html
http://www.cnblogs.com/CCBB/archive/2010/12/29/1920884.html
https://github.com/cran/tvR/blob/7e8f900b99cdae8e65774b166423dbd39a07f6a5/src/RcppCollection_Image.cpp