维盟FBM-220不死机固件 WAYOS FBM220稳定固件.
升级说明:
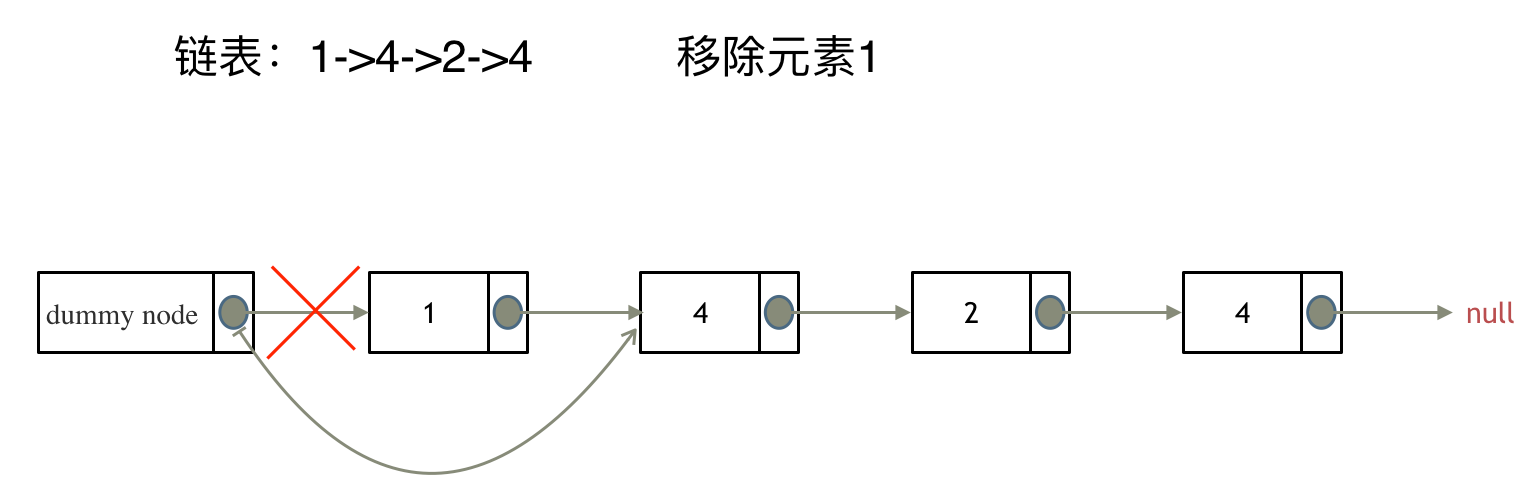
先单机上网下载此固件,然后把路由复位,断掉所有外网 WAN。(一定要先复位路由)
以上两步完成后进入路由WEB管理页进行升级,请耐心等待升级完成。然后在管理页面找到恢复出厂设置。等待路由就绪后开始配置路由器。注:不要使用之前导出的配置。
文件:url80.ctfile.com/f/25127180-730542283-daaa40?p=551685 (访问密码: 551685)
题意
构造两个长为 n 排列,使得两排列有长为 a 公共前缀和长为 b 的公共后缀。
题解
知识点:构造。
注意到,当 a+b≤n−2 时,中间段至少有两个位置可以操作使其不同,于是公共前后缀可以分别满足互不影响;否则,公共前后缀必然交叉,此时只有 a=n,b=n 的情况。
时间复杂度 O(1)
空间复杂度 O(1)
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
bool solve() {
int n, a, b;
cin >> n >> a >> b;
if (n - a - b >= 2 || a == n && b == n) cout << “Yes” << ‘\n’;
else cout << “No” << ‘\n’;
return true;
}
int main() {
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t–) {
if (!solve()) cout << -1 << ‘\n’;
}
return 0;
}
B
题意
给定一个环,初始时每个元素一定不同于它的相邻元素。
每次操作可以删除一个元素,删除后环合并,相同的相邻元素会立刻消失。
问最多能操作几次。
题解
知识点:构造。
当环中只含有两种不同的元素,那么每次删除(除了最后两次)都会再额外消失一个,那么最终答案是 n2+1 。
当环中至少含有三种不同的元素,我们发现这类环一定存在三个连续的不同元素。
我们可以找到两个元素 ai,aj(i≠j) ,满足 ai=aj 且 ai 有两个不同的相邻元素 ,然后删除 ai,直到不存在这样两个元素。
最后,至少有一种元素只剩下一个。如果所有种类的元素都至少有两个,因为一定存在三个连续的不同元素,那么这三个元素中间的那个元素满足有相同元素,且这个元素的相邻元素不同,所以我们可以按上述操作继续删。
我们可以以这个元素作为中心,持续删它的相邻元素。因为这个元素只有这一个,就不存在环合并后相邻元素相同的情况,所以最后没有元素是操作后额外消失的,答案是 n 。
时间复杂度 O(nlogn)
空间复杂度 O(n)
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
bool solve() {
int n;
cin >> n;
set st;
for (int i = 1;i <= n;i++) {
int x;
cin >> x;
st.insert(x);
}
if (st.size() >= 3) cout << n << ‘\n’;
else cout << n / 2 + 1 << ‘\n’;
return true;
}
int main() {
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t–) {
if (!solve()) cout << -1 << ‘\n’;
}
return 0;
}
C
题意
给出一个 n×n 的关系矩阵 b ,根据 b 构造 n 个非空集合 Ai 。
bi,j=1 时表示 Ai⊂Aj ,其他情况 bi,j=0 。
Ai 中的元素只能是 [1,n] 中的整数。
题解
知识点:构造,STL。
为了使得每个集合与其它没有关系的集合之间始终是独立的,我们先给每个集合加入一个唯一的元素,为了方便可以一开始 Ai={i} 。
这样以后,我们对 b 遍历,对于 Ai⊂Aj 可以让 Aj=Ai∪Aj 。
最后,两个互不相干的集合 Ai,Aj 在合法的关系 b 之下一定不会有关,因为 Ai 不会有 Aj 的独立元素 j ,反之亦然。
用 bitset 实现会很舒服qwq。
时间复杂度 O(n3)
空间复杂度 O(n2)
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
bool b[107][107];
bitset<107> bs[107];
bool solve() {
int n;
cin >> n;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) {
char ch;
cin >> ch;
b[i][j] = ch == ‘1’;
}
}
for (int i = 1;i <= n;i++) {
bs[i].reset();
bs[i][i] = 1;
}
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) {
if (b[i][j]) bs[j] |= bs[i];
}
}
for (int i = 1;i <= n;i++) {
cout << bs[i].count() << ’ ';
for (int j = 1;j <= n;j++)if (bs[i][j]) cout << j << ’ ';
cout << ‘\n’;
}
return true;
}
int main() {
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t–) {
if (!solve()) cout << -1 << ‘\n’;
}
return 0;
}
D
题意
f(a,b) 为 a+b 时发生进位的二进制位的数量。
求有序对 (a,b) 满足 a,b∈[0,2n) 时, f(a,b)=k 的数量。
题解
方法一
知识点:排列组合,数学。
我们考虑发生进位位置对答案的影响。
设 ai,bi 分别为 a,b 的二进制第 i 位(从 1 开始),ci 表示 a+b 在第 i 位(从 1 开始)是否进位。另外,c0=0 方便之后计数。
显然只有以下四种情况:
如果 ci=0,ci−1=1 ,那么可以推断 (ai,bi)=(0,0) 。
如果 ci=1,ci−1=0 ,那么可以推断 (ai,bi)=(1,1) 。
如果 ci=ci−1=1 ,那么可以推断 (ai,bi) 有三种组合:(0,1),(1,0),(1,1) 。
如果 ci=ci−1=0 ,那么可以推断 (ai,bi) 有三种组合:(0,1),(1,0),(0,0) 。
进一步考虑 c ,其一定形如 101000…110011100|0 (从右往左)。假设有 m 个位置 ci≠ci−1,i∈[1,n] ,那么可以归纳得出,有 m+1 个交替的连续 01 段。
其中,进位段(连续 1 段)有 ⌊m+12⌋ 个,不进位段(连续 0 段)有 ⌈m+12⌉ 个,有三种组合的自由位有 n−m 个。因此,我们隔板法求出 k 个进位分成 ⌊m+12⌋ 个连续段的方案数 C⌊m+12⌋−1k−1 和剩下 n+1−k 个不进位分成 ⌈m+12⌉ 个连续段的方案数 C⌈m+12⌉−1n+1−k−1 ,以及求出自由位贡献 3n−m ,将三种方案乘法原理组合在一起就是有 m 个位置 ci≠ci−1,i∈[1,n] 的答案。
最后 m∈[0,n] 枚举一下求和即可。其中两个隔板法的组合数要特判 C0−10−1 的情况,这种情况设为 1 ,其他不合法情况设为 0 。
时间复杂度 O(nlogn)
空间复杂度 O(n)
方法二
知识点:排列组合,数学。
方法二思维量更少一点。
我们直接讨论 k 个进位连续段分成 i 个连续段的情况,以及显然进位段和不进位段是交替的。
首先,会有 i 个位置必须设为 (1,1) ,因为有 i 个进位段。其次,如果不进位段右侧有进位段,则不进位段因为需要阻止进位段继续进位,右端必须设为 0 。
我们需要分别考虑前导和后导是否是进位段的自由位情况。因为前导不进位时,i 个进位段左侧都有不进位段,自由位有 n−2i 个;前导进位时,只有 i−1 个进位段左侧有不进位段,前导进位段左侧天然是 0 ,自由位有 n−2i+1 个。
进一步,考虑四类段分配情况。以前导后导都不进位为例,则有 i 段进位段和 i+1 段不进位段,组合数求一下就行,其他以此类推。
时间复杂度 O(nlogn)
空间复杂度 O(n)
代码
方法一
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e9 + 7;
int qpow(int a, int k) {
int ans = 1;
while (k) {
if (k & 1) ans = 1LL * ans * a % mod;
k >>= 1;
a = 1LL * a * a % mod;
}
return ans;
}
int fact[1000007], factinv[1000007];
void init(int n) {
fact[0] = 1;
for (int i = 1;i <= n;i++) fact[i] = 1LL * i * fact[i - 1] % mod;
factinv[n] = qpow(fact[n], mod - 2);
for (int i = n;i >= 1;i–) factinv[i - 1] = 1LL * factinv[i] * i % mod;
}
int C(int n, int m) {
if (n == m && m == -1) return 1;
if (n < m || m < 0) return 0;
return 1LL * fact[n] * factinv[n - m] % mod * factinv[m] % mod;
}
bool solve() {
int n, k;
cin >> n >> k;
init(n);
int ans = 0;
for (int i = 0;i <= n;i++) {
ans = (ans + 1LL * C(k - 1, (i + 1) / 2 - 1) * C(n + 1 - k - 1, (i + 2) / 2 - 1) % mod * qpow(3, n - i) % mod) % mod;
}
cout << ans << ‘\n’;
return true;
}
int main() {
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t = 1;
//cin >> t;
while (t–) {
if (!solve()) cout << -1 << ‘\n’;
}
return 0;
}
方法二
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e9 + 7;
int qpow(int a, int k) {
int ans = 1;
while (k) {
if (k & 1) ans = 1LL * ans * a % mod;
k >>= 1;
a = 1LL * a * a % mod;
}
return ans;
}
int fact[1000007], factinv[1000007];
void init(int n) {
fact[0] = 1;
for (int i = 1;i <= n;i++) fact[i] = 1LL * i * fact[i - 1] % mod;
factinv[n] = qpow(fact[n], mod - 2);
for (int i = n;i >= 1;i–) factinv[i - 1] = 1LL * factinv[i] * i % mod;
}
int C(int n, int m) {
if (n < m || m < 0) return 0;
return 1LL * fact[n] * factinv[n - m] % mod * factinv[m] % mod;
}
bool solve() {
int n, k;
cin >> n >> k;
if (k == 0) {
cout << qpow(3, n) << ‘\n’;
return true;
}
init(n);
int ans = 0;
for (int i = 1;i <= k;i++) {
if (n - 2 * i >= 0) {
//前导不进位,后导不进位
ans = (ans + 1LL * C(n - k - 1, i) * C(k - 1, i - 1) % mod * qpow(3, n - 2 * i) % mod) % mod;
//前导不进位,后导进位
ans = (ans + 1LL * C(n - k - 1, i - 1) * C(k - 1, i - 1) % mod * qpow(3, n - 2 * i) % mod) % mod;
}
if (n - 2 * i + 1 >= 0) {
//前导进位,后导不进位
ans = (ans + 1LL * C(n - k - 1, i - 1) * C(k - 1, i - 1) % mod * qpow(3, n - 2 * i + 1) % mod) % mod;
//前导进位,后导进位
ans = (ans + 1LL * C(n - k - 1, i - 2) * C(k - 1, i - 1) % mod * qpow(3, n - 2 * i + 1) % mod) % mod;
}
}
cout << ans << ‘\n’;
return true;
}
int main() {
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t = 1;
//cin >> t;
while (t–) {
if (!solve()) cout << -1 << ‘\n’;
}
return 0;
}