作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:笔试强训选择题
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!
文章目录
前言
一、Day23习题(错题)解析
1.
2.
3.D
4.
5.
6.C
7.
8.
9.
10.
总结

前言
一、Day23习题(错题)解析
1.

解析:C
解题思路:
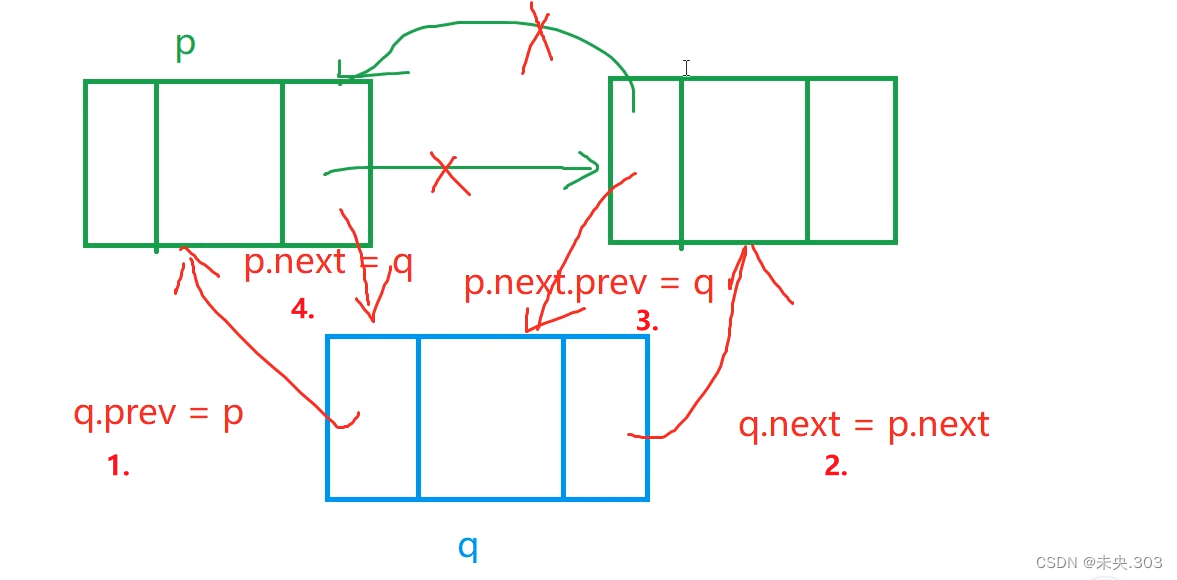
本题涉及双向循环链表中进行插入新的节点;
就要涉及结点的操作改变来插入新的结点;
图示说明:
2.

解析:A
解题思路:
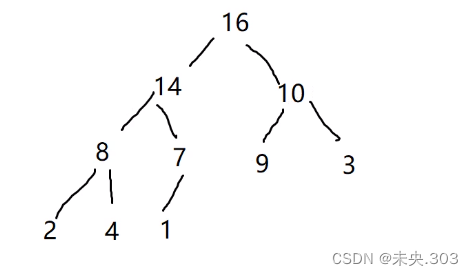
我们将上述序列按完全二叉树进行排列:
我们发现 此排列方式满足的是大根堆(大顶堆)的排列方式;
3.D

4.

解析:D
相关知识点:
A:递归次数与初始数据的有序性有关;
BCD:不管处理较长还是处理较短的分区,最终的处理次数是加起来的,与处理顺序无关;
5.

解析:D
解题思路:
本题比较巧妙;
第6层有9个叶子结点,此时求的是最大结点个数,认为存在第7层,且第6层排满的。
而前6层的总节点个数2^6 -1 = 63;
第6层本身有2^(6-1) =32,除去9个叶子结点其他23个结点都是度为2的结点;
所以得出第7层,23*2 = 46;所以总结点数:63+46= 109;
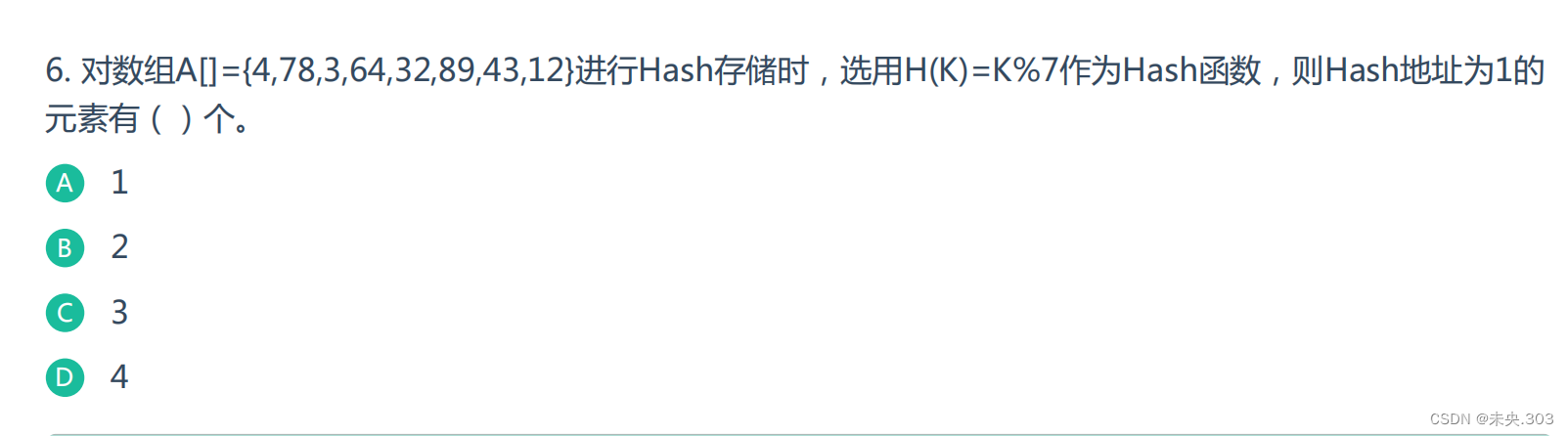
6.C
7.

解析:D
解题思路:
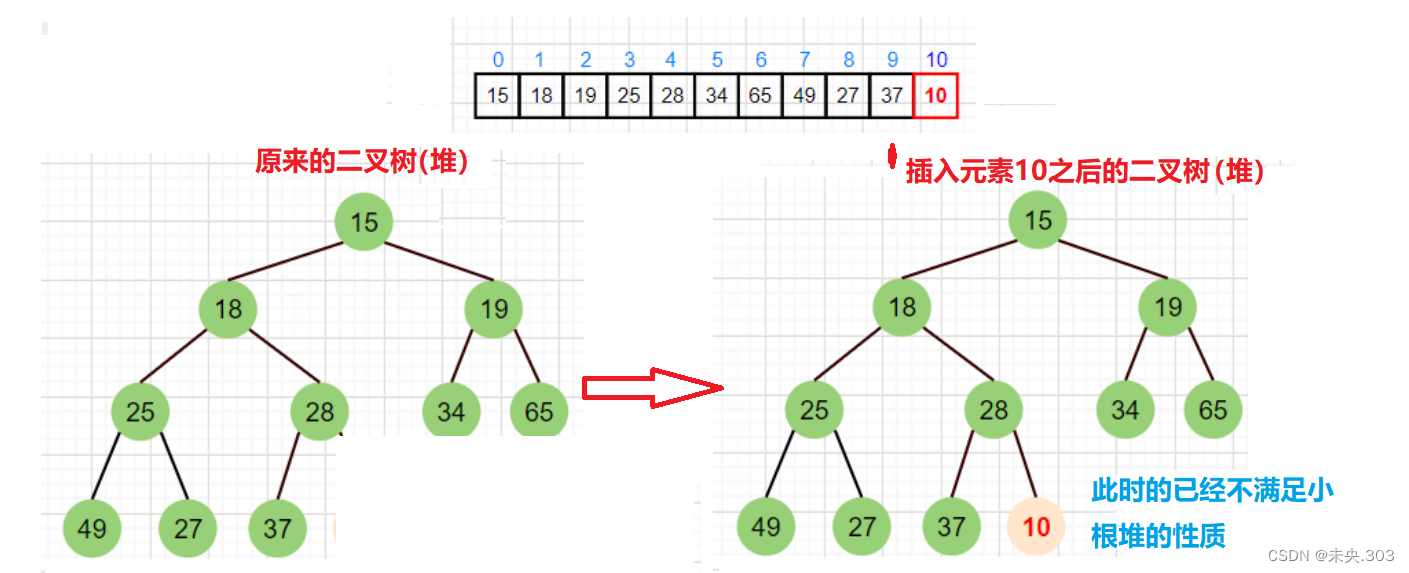
本题主要考察对于最小堆插入操作的调整;
图示说明:
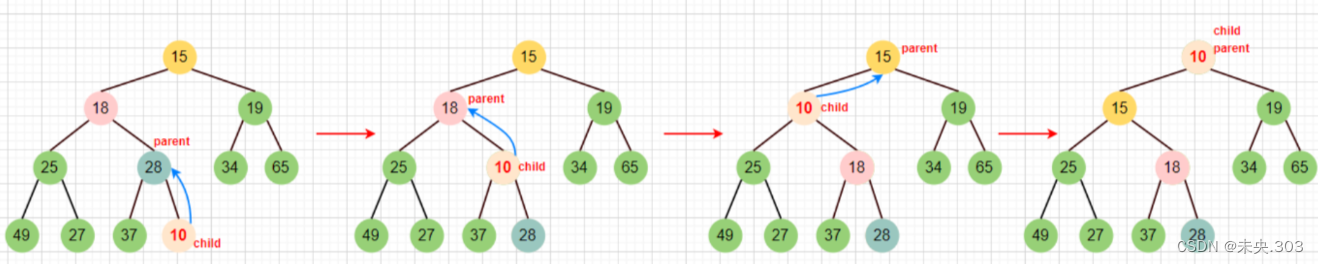
为了确保在插入数字10后依然是个小根堆,所以要将10和28交换,依次比较父结点parent和子结点child的大小,当父小于子结点的时候,就返回,反之就一直交换,直到根部。
由前文的得知的规律,parent = (child - 1) / 2,我们可以从下到上调整子树,不断的更新child和parent下标,直到根部15;
🔔需要注意的是:我们操控的是数组,但要把它想象成二叉树。
画图演示调整过程:
8.

解析:C
解题思路:
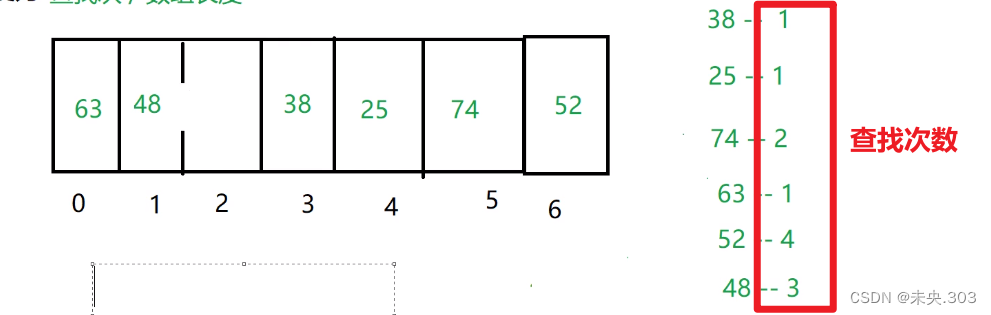
本题要求的是平均查找长度,平均查找长度=查找的总次数/数组长度;
我们需要将线性表中的每一个数计算其散列地址,然后采用线性探测法查找每个数所需的次数,最后计算其平均查找长度;
首先根据散列函数h(key) = key%7进行计算出散列地址:
38——3;25——4;74——5;63——0;52——6;48——1;
然后根据地址来找到每个数需要的查找次数:
最后根据公式计算即可得:平均查找次数=2次;
9.

解析:B
相关知识点:快速排序
链接转入:快速排序Java
10.

解析:D
相关知识点:
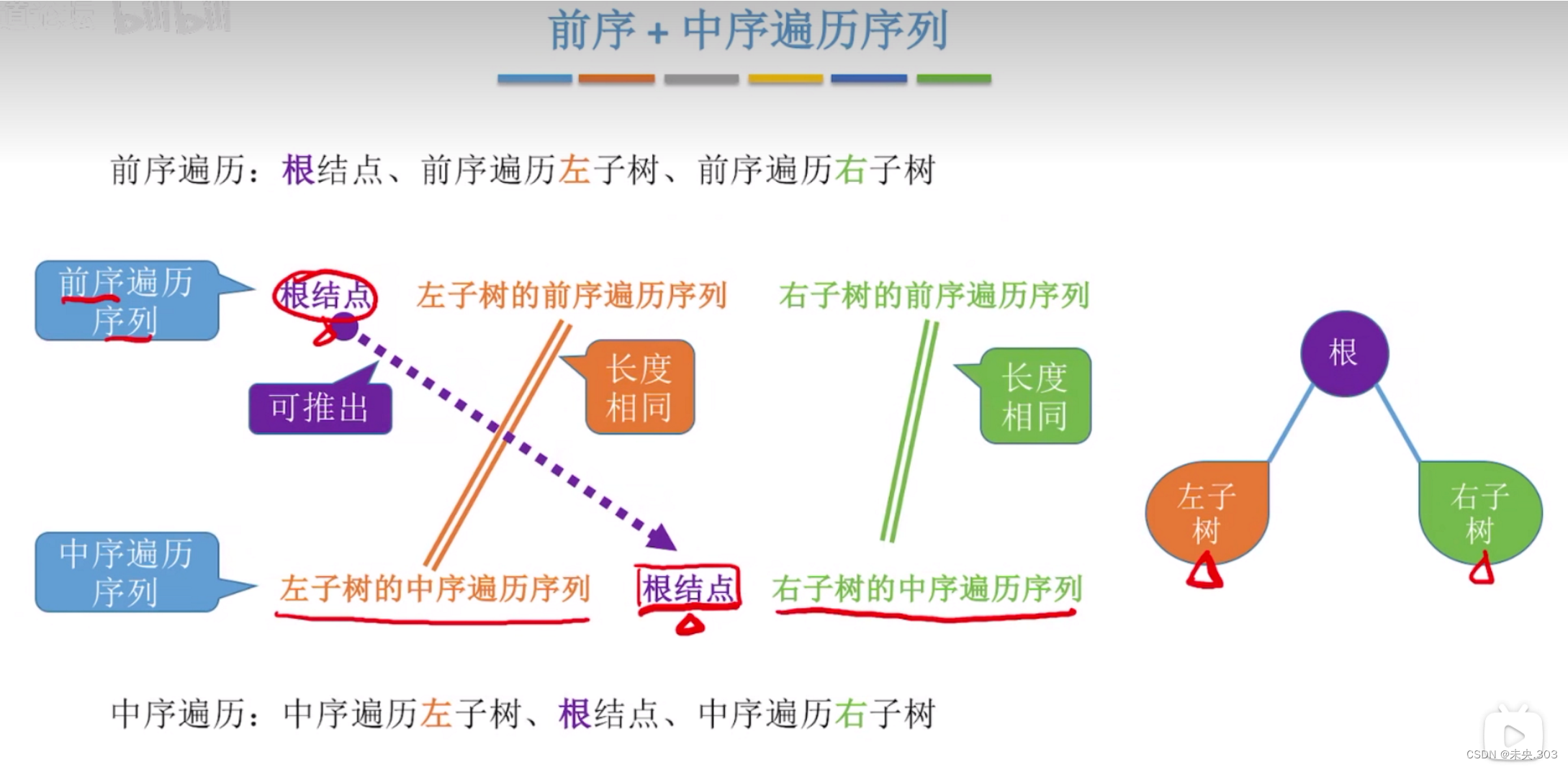
二叉树已知前序遍历和中序遍历求其后续遍历;
应该先由前中序遍历求原二叉树,再求其后续遍历;
前中序遍历求原二叉树方法:
求其后续遍历;
总结