A题

题解

对于x特判一下就好

代码

void solve()
{ll x,d;cin>>n>>m>>x>>t>>d;if(n>m){n=min(n,x);if(n<m){cout<<t;return;}cout<<(m-n)*d+t;}else{m=min(m,x);cout<<(m-n)*d+t;}return;
}

B

~~三角函数全还给高中老师了~~

题解

上图!
B题解
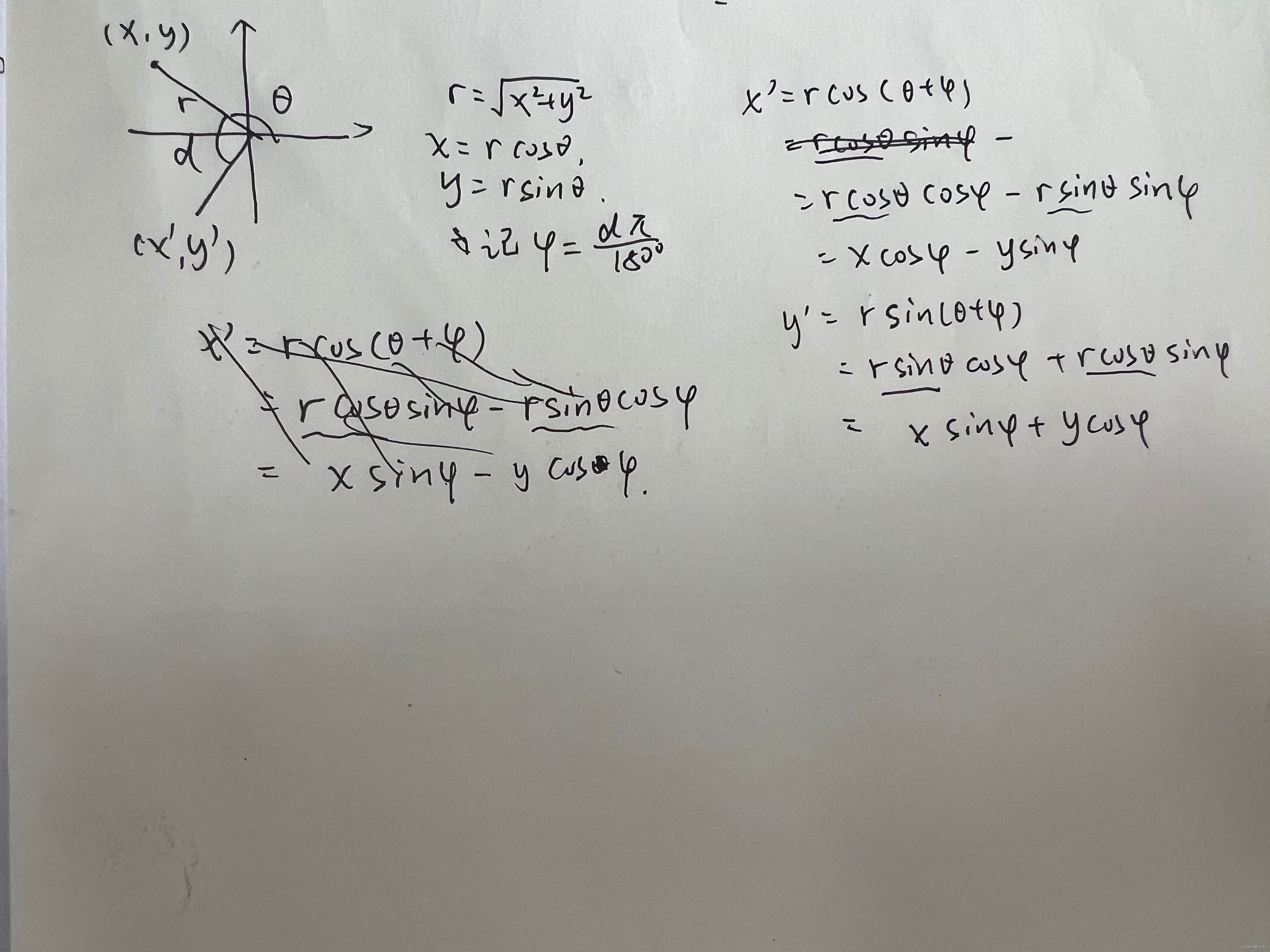
根据上图的结论, 可以得到

 x=a*cos(d)-b*sin(d);y=a*sin(d)+b*cos(d);

代码

void solve()
{cin>>n>>m>>cnt;double s=2.0*M_PI*cnt/360;double x,y;x=1.0*n*cos(s)-1.0*m*sin(s);y=1.0*n*sin(s)+1.0*m*cos(s);// cout<<<<endl;printf("%.8lf %.8lf",x,y);return;
}

C

翻译的题面有点错误, 这里就不放图了

题意

给出两个串a和b, 可以在a中任意两个相同的字符中插入一个相同的字符, 问是否可以使得a==b

题解

双指针
从下标0开始, a和b串都直接向后找不同的字符并记录相同的字符串有多少个
假设a向后找到第一一个与前面不同的字符为a1
b向后找到第一一个与前面不同的字符为b1
a中相同的字符数量为a2
b中相同的字符数量为b2

a1!=b1 显而易见此时再怎么操作也不可能使得a==b
a2=0且b2=0 不需要操作
a2>0且b2>0且a2<b2 将a2操作到a2==b2为止即可
a2=0且b2>0 无法操作但却需要操作的情况
a2>0&&b2>0&&a2>b2 操作只能添加不能减少
最后需要特判b的指针是否走到了终点

1 4 5都是错误的, 6需要额外判断

代码

~~写的什么一坨屎, 没有技巧只有特判是吧~~

void solve()
{cin>>s1>>s2;cnt=s2.size();ll j=0;for(int i=0;i<s1.size();i++){ll a,b;a=b=0;while(i<s1.size()-1&&s1[i]==s1[i+1]){a++;i++;} while(j<s2.size()-1&&s2[j]==s2[j+1]){b++;j++;}// cout<<i<<s1[i]<<' '<<j<<s2[j]<<endl;if(s1[i]!=s2[j]) {noreturn;}if(a==0&&b>0){noreturn;}if(a>b){noreturn;}j++;}if(j!=s2.size()) {noreturn;}yesreturn;
}

D

题意

有n个圆, s点和t点都在某两个圆上, 问s0是否能通过圆周走到t位置

题解

暴力 $n^{2}$ 求每两个圆之间是否连通, 使用并查集存储连通的状态
有点像kruskal但并不需要求最小只需要连通 (~~那不就是单纯的并查集吗~~)

代码

ll find(ll x)
{if(x!=arr[x]) arr[x]=find(arr[x]);return arr[x];
}ll cal(ll x)
{return x*x;
}void solve()
{cin>>n;ll sx,sy,tx,ty,ans1,ans2;cin>>sx>>sy>>tx>>ty;rep(i,1,n) cin>>x[i]>>y[i]>>r[i];rep(i,1,n){arr[i]=i;if(cal(x[i]-sx)+cal(y[i]-sy)==cal(r[i])) ans1=i;if(cal(x[i]-tx)+cal(y[i]-ty)==cal(r[i])) ans2=i;}rep(i,1,n)rep(j,i+1,n){if(cal(x[i]-x[j])+cal(y[i]-y[j])>cal(r[i]+r[j])) continue;if(cal(x[i]-x[j])+cal(y[i]-y[j])<cal(r[i]-r[j])) continue;ll a,b;a=find(i);b=find(j);arr[a]=b;}if(find(ans1)==find(ans2)) yeselse noreturn;
}