一棵有点自律的树——搜索二叉树

news/2024/11/13 15:43:47/

在这里插入图片描述

文章目录

  • 💐专栏导读
  • 💐文章导读
  • 🌷搜索二叉树概念
  • 🌷二叉搜索树的构建
    • 🌺查找操作
    • 🌺插入操作
    • 🌺删除操作
    • 🌺遍历操作
    • ☘️测试
  • 🏵️拓展——递归实现
    • 🍃递归查找
    • 🍃递归插入
    • 🍃递归删除
  • ❄️完整源码
    • 🐙非递归版
    • 🐌递归版本

💐专栏导读

🌸作者简介：花想云，在读本科生一枚，致力于 C/C++、Linux 学习。

🌸本文收录于 C++系列，本专栏主要内容为 C++ 初阶、C++ 进阶、STL 详解等，专为大学生打造全套 C++ 学习教程，持续更新！

🌸相关专栏推荐：C语言初阶系列 、C语言进阶系列 、数据结构与算法、Linux从入门到精通

💐文章导读

本章我们将认识一种新的二叉树——搜索二叉树。这棵树有个神奇的功能就是会对数据自动排序且有着非常高的查找效率。搜索二叉树作为set、map的基础结构，同样又是接下来将要学到的AVL树以及红黑树的实现基础非常值得我们去深入学习~

在这里插入图片描述

🌷搜索二叉树概念

二叉搜索树本质上也是一种二叉树，只不过多了一个约束规则——

若一棵二叉树不为空，则：

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值；
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值；
  • 它的左右子树也分别为搜索二叉树；

所以构建一个搜索二叉树，只需要在插入结点时满足约束规则即可。

🌷二叉搜索树的构建

与二叉树相同，二叉搜索树由一个个结点链接而成。每个结点包含三个成员——

  • _left（左孩子）；
  • _right（有孩子）；
  • _key（键值）；

所以首先定义一个BSTNode（Binary Search Tree简写）结构体——

template <class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key) // 构造函数:_left(nullptr), _right(nullptr), _key(key){}
};

同样的，再定义一个搜索二叉树的类，即class BSTree——

template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:// 成员函数的实现// 插入、删除、查找...
private:Node* _root = nullptr;
};

接着就是各种成员函数的实现了~

🌺查找操作

搜索二叉树的查找比较简单而且更容易帮助我们理解搜索二叉树的性质，所以先从查找入手。

在这里插入图片描述

以上图为例，倘若我们要查找 7，具体的思路是这样的——

  1. 7 < 8，因此去 8 的左子树去查找；
  2. 7 > 3，因此去 3 的右子树去查找；
  3. 7 > 6，因此去 6 的右子树去查找；
  4. 7 = 7，找到了，返回true；

于是我们试着着手实现一个Find函数。

bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key) // 大于则去右子树查找cur = cur->_right;else if (cur->_key > key) // 小于则去左子树查找cur = cur->_left;elsereturn true; // 找到返回true}return false; // 未找到返回false
}

🌺插入操作

理解了如何查找，插入也就非常简单。
在这里插入图片描述
还是以此图为例，倘若我们要插入 9 ，具体步骤为——

  1. 首先确定cur的位置，并随时更新parent；
  2. 最终，cur走到10的左节点的位置，即cur = nullptr，循环结束；
  3. 此时patent = Node*(10)；
  4. 最后一步，new一个结点Node*(key)并赋值给parent->_left即可。
bool Insert(const K& key)
{// 如果是第一次插入，直接new一个新结点给_rootif (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root; // cur用来定位插入的位置Node* parent = cur; // 记录parent的父亲while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if(cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}// 插入cur = new Node(key);// 插入时依旧要进行判断if (parent->_key < key)parent->_right = cur;elseparent->_left = cur;return true;
}

🌺删除操作

二叉搜索树的删除是最精华的部分。对与叶子节点，例如4、7、13，删除非常简单，只需将自身的位置替换为nullptr即可。

在这里插入图片描述
如果要删除14或者10，也是比较简单的，因为10的左右子树只有一方为nullptr（10的左子树为空），所以只需要载删除的时候让父结点接管自己不为空的子树即可。

倘若要删除6或者3，由于它们的左右子树都不为空，删除时无法将两个子树都交给父结点，情况就较为复杂。

所以此种情况，我们只能想办法请一个人来接替自己的位置，但是并不是谁来都能胜任这个位置的。这个接替者必须满足二叉搜索树的条件——左子树都比它小，右子树都比它大。那么这个接替者的人选只能有这两个——

  • 左子树的最大（最右）节点；
  • 或右子树的最小（最左）节点；

例如，倘若要删除3，此时有两种做法都可行——

  1. 用1替换3；
  2. 用7替换3；

综上所述，删除操作共分为一下几种情况——

  1. 左子树为空；
  2. 右子树为空；
  3. 左右子树都不为空 ；
  4. （左右子树都为空其实可以归并到1或2的情况中）；
bool Erase(const K& key)
{Node* cur = _root;Node* parent = cur;while (cur){// 找到值为key的结点if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else // 找到了{	// 删除if (cur->_left == nullptr) // 1.左子树为空{if (cur == _root) // 根节点的删除{_root = cur->_right;return true;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;}}else if (cur->_right == nullptr) // 2.右子树为空{if (cur == _root) // 根节点的删除{_root = cur->_left;return true;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;}}else // 左右子树都不为空{// 找左子树的最大结点 或者 右子树的最小结点Node* minRight = cur->_right;Node* pminRight = cur;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key; // 替换if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;
}

🌺遍历操作

最后，二叉搜索树的遍历非常简单，就是之前学习过的二叉树的中序遍历。

void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);
}

注：由于调用函数时C++封装的特性，需设计两个函数，InOrder接口对外提供，-—_InOrder不对外提供。

☘️测试

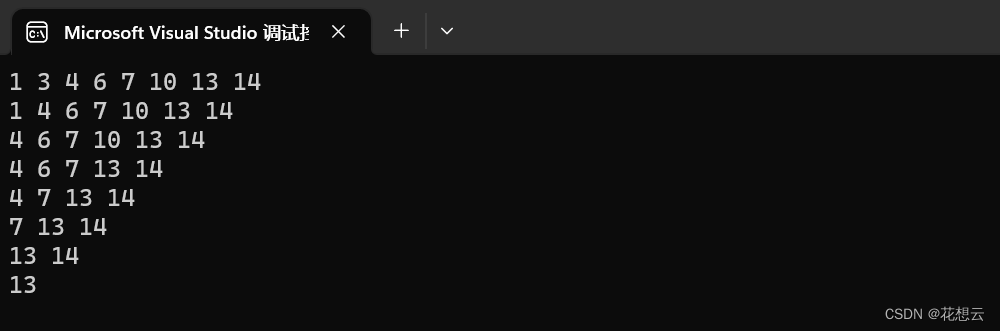
在这里插入图片描述

我们可以构建一棵这样的搜索二叉树，再对每一个结点进行删除操作，验证代码是否正确~

void BTreeTest()
{BSTree<int> tree;int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };for (auto e : a){tree.InsertR(e);}for (auto e : a){tree.EraseR(e);tree.InOrder();}
}

在这里插入图片描述

🏵️拓展——递归实现

对于搜索二叉树来说，上面实现的非递归版本是比递归版本更优的。此处的递归实现完全属于多余了，但是作为拓展内容看一看也未尝不可。

🍃递归查找

bool FindR(const K& key)
{return _FindR(_root, key);
}bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key > key)_FindR(root->_left, key);else_FindR(root->_right, key);
}

🍃递归插入

bool EraseR(const K& key)
{return _EraseR(_root, key);
}bool _InsertR(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;
}

🍃递归删除

bool EraseR(const K& key)
{return _EraseR(_root, key);
}bool _EraseR(Node*& root,const K& key)
{if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* maxLeft = root->_left;while (maxLeft->_right)maxLeft = maxLeft->_right;std::swap(root->_key, maxLeft->_key);return _EraseR(root->_left, key);}delete del;return true;}
}

❄️完整源码

🐙非递归版

#include<iostream>
using namespace std;template <class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree() = default;bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if(cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}// 插入cur = new Node(key);if (parent->_key < key)parent->_right = cur;elseparent->_left = cur;return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key)cur = cur->_right;else if (cur->_key > key)cur = cur->_left;elsereturn true;}return false;}bool Erase(const K& key){Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;return true;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;}}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;return true;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;}}else{// 找左子树的最大结点 或者 右子树的最小结点Node* minRight = cur->_right;Node* pminRight = cur;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}
protected:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);}
private:Node* _root = nullptr;
};

🐌递归版本

#pragma once
#include<iostream>
using namespace std;template <class K>
struct BSTreeNode
{BSTreeNode* _left;BSTreeNode* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree() = default;void InOrder(){_InOrder(_root);cout << endl;}bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}
protected:bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key > key)_FindR(root->_left, key);else_FindR(root->_right, key);}bool _EraseR(Node*& root,const K& key){if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* maxLeft = root->_left;while (maxLeft->_right)maxLeft = maxLeft->_right;std::swap(root->_key, maxLeft->_key);return _EraseR(root->_left, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);}
private:Node* _root = nullptr;
};

在这里插入图片描述

⭐抽奖活动⭐

抽奖文章链接——Spring Cloud——演进与应用的分布式系统开发利器（文末赠书3册）

⭐感谢赞助⭐

618，清华社 IT BOOK 多得图书活动开始啦！活动时间为2023年6月7日至6月18日，清华社为您精选多款高分好书，涵盖了C++、Java、Python、前端、后端、数据库、算法与机器学习等多个IT开发领域，适合不同层次的读者。全场5折，扫码领券更有优惠哦！

优惠购书请戳这里

在这里插入图片描述


http://www.ppmy.cn/news/312897.html

相关文章

python中的高阶函数讲解

python中的高阶函数讲解

文章目录 函数的说明将函数作为参数的高阶函数匿名函数filter()函数引入lambda函数map()函数sort()函数sorted()函数 将函数作为返回值的高阶函数闭包 函数的说明 # 函数式编程 # - 在Python中&#xff0c;函数是一等对象 # - 一等对象一般都会具有如下特点&#xff1a…
阅读更多...
CSR8670 spi方式软件烧录方法

CSR8670 spi方式软件烧录方法

1 2
阅读更多...
csr8670 (1)

csr8670 (1)

csr 是英国的一家蓝牙芯片公司。csr8670是最新的4.0芯片。 蓝牙最重要的应用就是我们常见的蓝牙耳机。蓝牙耳机可分为两种。 1.单声道 主要基于hfp,hsp协议&#xff0c; 2. 立体声 a2dp 协议&#xff0c;当然也要有hfp,hsp协议。 以上的各种协议是高层协议&#xff0c;下…
阅读更多...
QCC3040一拖二发射器（aptXLL）replace CSR8670

QCC3040一拖二发射器（aptXLL）replace CSR8670

QCC3040一拖二发射器&#xff08;aptXLL&#xff09;替代CSR8670 蓝牙版本Ver5.2&#xff0c;支持USB音频输入&#xff0c;支持模拟输入&#xff0c;支持光纤模式&#xff08;另加转换硬件&#xff09;&#xff0c;支持aptXLL、aptXHD&#xff0c;aptX&#xff0c;SBC&#xf…
阅读更多...
RTL8367SC单芯片做千兆2光5电

RTL8367SC单芯片做千兆2光5电

最近在调试RTL8367SC&#xff0c;本以为之前很熟悉RTL8367S&#xff0c;对RTL8367SC的配置应该很容易的事&#xff0c;结果对RTL8367SC的寄存器研究才发现&#xff0c;与RTL8367S有太多不一样的地方&#xff0c;RTL8367S有的寄存器&#xff0c;在RTL8367SC里已经删除&#xff0…
阅读更多...
CSR8670/CSR8675多国语言字库显示逻辑

CSR8670/CSR8675多国语言字库显示逻辑

CSR8670/CSR8675多国语言字库显示逻辑 系统框图 名词解释&#xff1a; OLED&#xff1a;一个128*64的IIC接口的显示模块。 FLASH&#xff1a;存放字库数据的闪存。 CSR8675/CSR8670:主控芯片&#xff0c;通过蓝牙AVRCP接收手机端歌名等歌曲属性&#xff0c;并从FLASH读取对…
阅读更多...
CSR8670项目实战：4人组网蓝牙对讲耳机

CSR8670项目实战：4人组网蓝牙对讲耳机

为了方便大家学习&#xff0c;现与我爱蓝牙网联合推出【QCC300x/CSR867x/QCC30xx/QCC51xx开发板】。 博主联系方式&#xff1a;Call-15715161220&#xff0c;QQ-705829339 技术交流QQ群号&#xff1a;743434463 开发板会员QQ群号&#xff1a;725398389&#xff08;凭订单号入群…
阅读更多...
CSR8670 学习记录

CSR8670 学习记录

CSR的工程文件介绍 Project 文件 xiw&#xff1a;xIDE的工作空间&#xff0c;一个工程有一个对应的工作空间 xip&#xff1a;VM文件&#xff0c;比如我们说的的speaker就是这个指的这个 mak&#xff1a;工程的makefile文件 sink figuratio…
阅读更多...
最新文章

Copyright @ 2022~2023