文章目录
- 一、Tanh
- 二、Sigmoid
- 三、ReLU
- 四、Leaky ReLU
- 五、ELU
- 六、SiLU
- 七、Mish
本文主要介绍卷积神经网络中常用的激活函数及其各自的优缺点
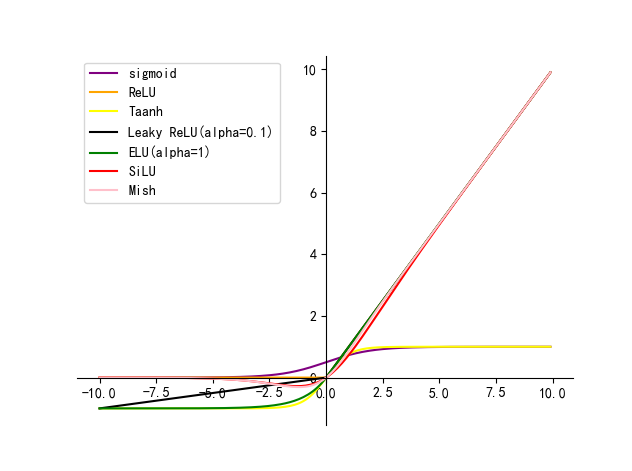
最简单的激活函数被称为线性激活,其中没有应用任何转换。 一个仅由线性激活函数组成的网络很容易训练,但不能学习复杂的映射函数。线性激活函数仍然用于预测一个数量的网络的输出层(例如回归问题)。
非线性激活函数是更好的,因为它们允许节点在数据中学习更复杂的结构 。两个广泛使用的非线性激活函数是 sigmoid 函数和 双曲正切 激活函数。
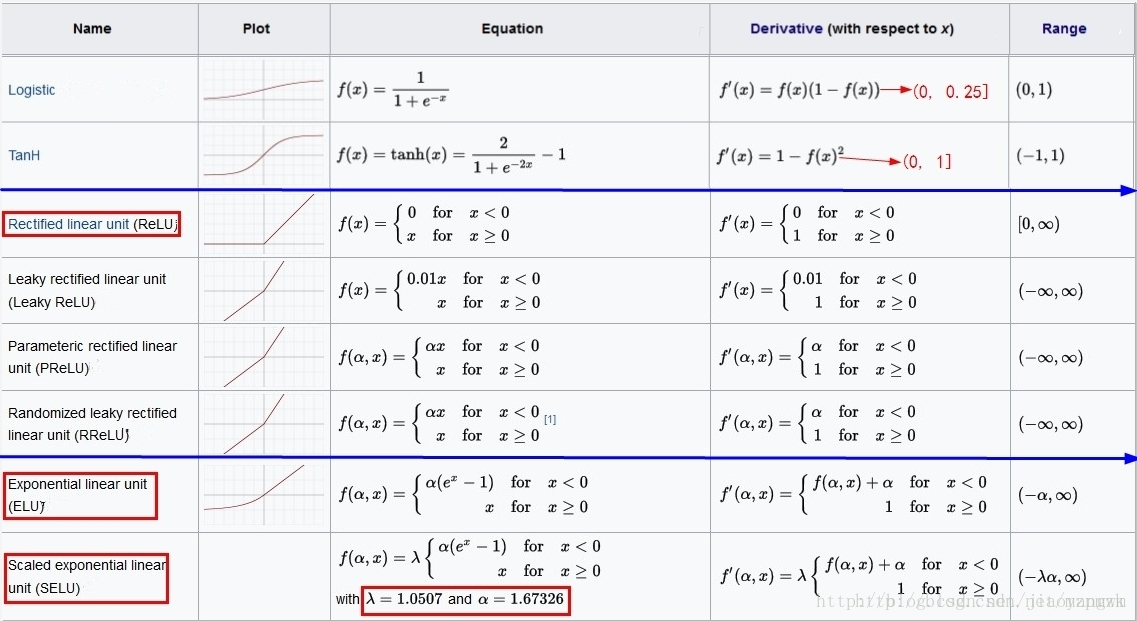
一、Tanh
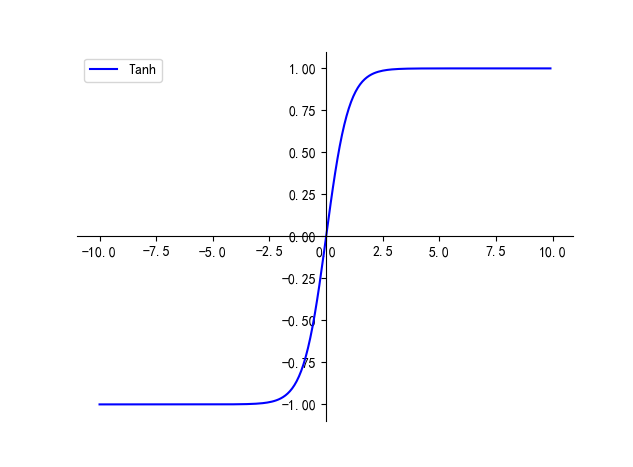
Tanh 函数公式如下,数值范围在 (-1, 1),导数范围为 (0, 1]
Tanh 函数的优点:
- 以 0 为中心,能够达到正负平衡,避免出现梯度的不稳定性
Tanh 函数的缺点:
- 会导致梯度消失问题!
二、Sigmoid

Sigmoid 函数公式如下,数值范围为 (0, 1),导数范围为 (0, 0.25]:
- f(x)=11+e−zf(x) = \frac{1}{1+e^{-z}}f(x)=1+e−z1
sigmoid 函数优点:
- 可以把输入映射到 (0, 1)区间,可以用来表示概率,在物理意义上最为接近生物神经元
sigmoid 函数缺点:
- 梯度消失问题 :由于 sigmoid 的导数 f′(zl) 区间为 (0, 0.25],所以其极易落入饱和区,导致梯度非常小,权重接近不变,无法正常更新
- sigmoid 的输出并不是均值为 0 的,所有输出数据的大于0,会增加梯度的不稳定性
- 当输出接近饱和或剧烈变化时,对输出范围的这种缩减往往会带来一些不利影响
三、ReLU
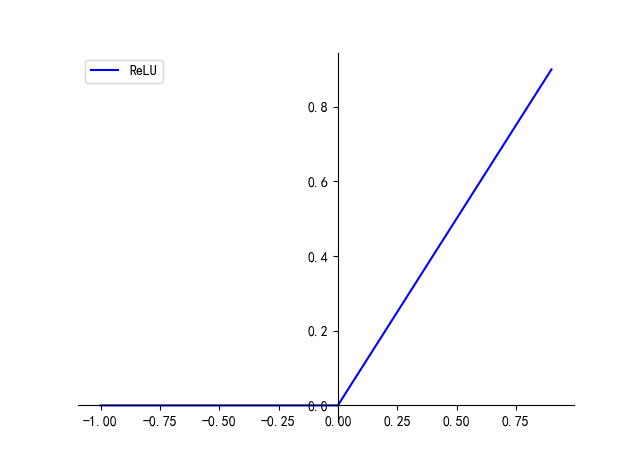
f(x)=max(0,x)f(x) = \text{max}(0, x)f(x)=max(0,x)
ReLU 函数的优点:
- 摒弃了复杂的计算, 比 sigmoid/tanh 收敛的更快 (大概快 6x)
- 其导数在其权重和(z) 大于 0 的时候为 1,不存在梯度消失现象权重可以正常更新,但也要防止 ReLU 的梯度爆炸
ReLU 函数的缺点:
- 小于 0 的输出经过 ReLU 之后会全都变成 0,梯度值为0,从而权重无法正常更新
- 输出具有偏移现象,即输出均值恒大于零
- 当使用了较大的学习速率时,易受到饱和的神经元的影响。
四、Leaky ReLU
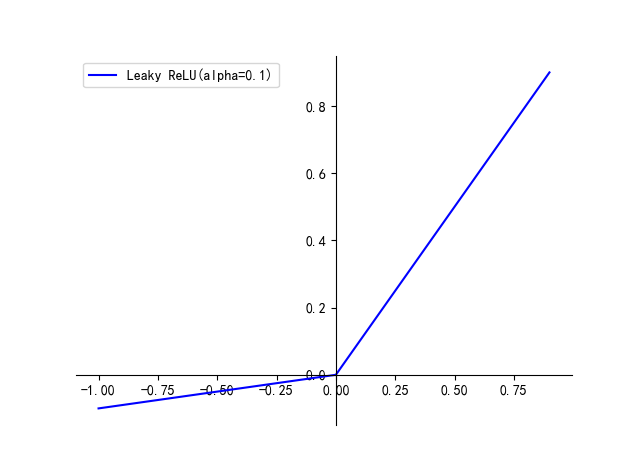
公式如下:
- f(x)=αx,x<0f(x) = \alpha x, \ x<0f(x)=αx, x<0
- f(x)=x,x>=0f(x) = x, \ x>=0f(x)=x, x>=0
为了防止模型 dead 的情况,出现了很多 ReLU 的改进版本,如 Leaky ReLU,在 0 右侧和 ReLU 一样,左侧从全零变成了一个斜率很小的直线
优点:
- 避免了小于零的特征被处理为 0 导致特征丢失的情况,同时左右两侧梯度都是恒定的,不会出现梯度消失现象
缺点:
- Leaky ReLU中的 α\alphaα 为常数,一般设置 0.01。这个函数通常比 ReLU 激活函数效果要好,但是效果不是很稳定,所以在实际中 Leaky ReLU 使用的并不多。
五、ELU
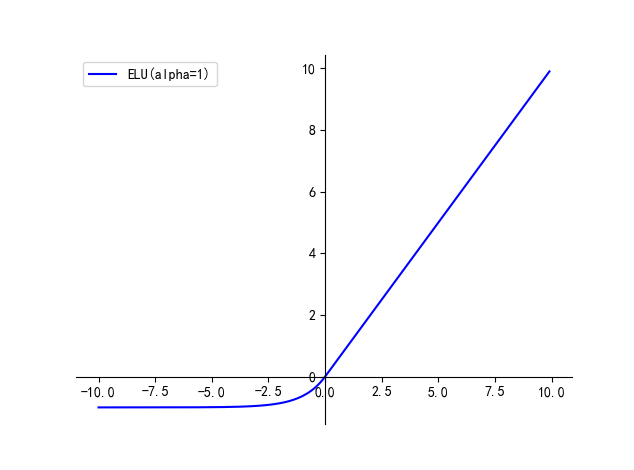
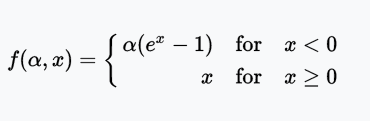
ELU(Exponential Linear Unit,指数线性单元)尝试加快学习速度。基于ELU,有可能得到比ReLU更高的分类精确度。
优点:
- 解决了 ReLU 可能导致的网络 dead 的问题
缺点:
- 计算量较大
六、SiLU
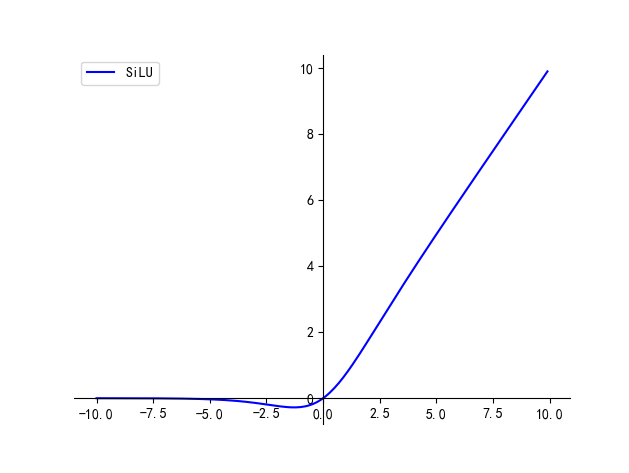
f(x)=x∗sigmoid(βx)f(x) = x *\text{sigmoid}(\beta x)f(x)=x∗sigmoid(βx),β=1\beta=1β=1 时就是 SiLU
优点:
- 相比 ReLU 增加了平滑性的特点
缺点:
- 引入了指数计算,增加了计算量
七、Mish
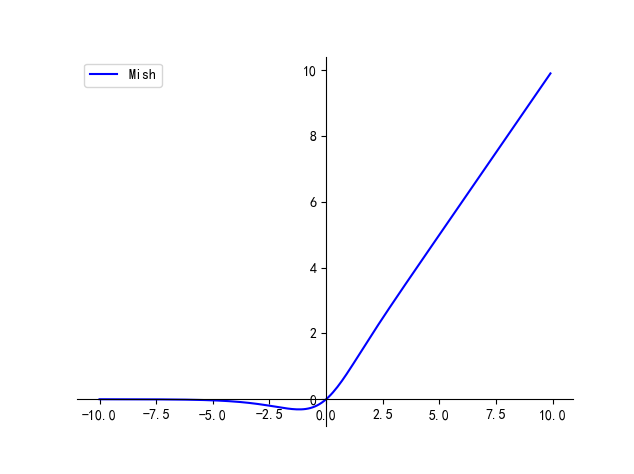
f(x)=x∗tanh(ln(1+ex))f(x) = x * \text{tanh}(\text{ln}(1+e^x))f(x)=x∗tanh(ln(1+ex))
优点:
- 平滑、非单调、无上界、有下界
缺点:
- 引入了指数函数,增加了计算量