1、功能实现与样本分析

       在数据挖掘领域，可以利用相应的算法对数据集进行训练，即对样本的特征进行分析，从而归纳出相同类别的样本之间存在的内在特征联系，进一步对未知类别的样本进行预测，判断出该样本所属的类别。本文实现了利用决策树算法对UCI 机器学习库上的经典wine数据集进行分类的目的。

       为达到相应的分类目的，需要先对数据集样本进行分析。

表1 wine数据集样本特征

      不用化学成分的含量与酒的所属类别息息相关。表1列举了所选用的wine数据集的特征情况。整个数据集样本包含13个特征，例如Alcohol(酒精度)，Malic acid（苹果酸含量）等，这些特征的取值范围见表1所示。

表2 wine数据集部分样本表

属性 1	属性 2	属性 3	属性 4	属性 5	属性 6	属性 7	属性 8	属性 9	属性 10	属性 11	属性 12	属性 13	类别
14.23	1.71	2.43	15.6	127	2.8	3.06	.28	2.29	5.64	1.04	3.92	1065	1
13.2	1.78	2.14	11.2	100	2.65	2.76	.26	1.28	4.38	1.05	3.4	1050	1
13.16	2.36	2.67	18.6	101	2.8	3.24	.3	2.81	5.68	1.03	3.17	1185	1
14.37	1.95	2.5	16.8	113	3.85	3.49	.24	2.18	7.8	.86	3.45	1480	1
13.24	2.59	2.87	21	118	2.8	2.69	.39	1.82	4.32	1.04	2.93	735	1
14.2	1.76	2.45	15.2	112	3.27	3.39	.34	1.97	6.75	1.05	2.85	1450	1
14.39	1.87	2.45	14.6	96	2.5	2.52	.3	1.98	5.25	1.02	3.58	1290	1
12.37	.94	1.36	10.6	88	1.98	.57	.28	.42	1.95	1.05	1.82	520	2
12.33	1.1	2.28	16	101	2.05	1.09	.63	.41	3.27	1.25	1.67	680	2
12.64	1.36	2.02	16.8	100	2.02	1.41	.53	.62	5.75	.98	1.59	450	2
13.67	1.25	1.92	18	94	2.1	1.79	.32	.73	3.8	1.23	2.46	630	2
12.37	1.13	2.16	19	87	3.5	3.1	.19	1.87	4.45	1.22	2.87	420	2
12.17	1.45	2.53	19	104	1.89	1.75	.45	1.03	2.95	1.45	2.23	355	2
12.37	1.21	2.56	18.1	98	2.42	2.65	.37	2.08	4.6	1.19	2.3	678	2
12.86	1.35	2.32	18	122	1.51	1.25	.21	.94	4.1	.76	1.29	630	3
12.88	2.99	2.4	20	104	1.3	1.22	.24	.83	5.4	.74	1.42	530	3
12.81	2.31	2.4	24	98	1.15	1.09	.27	.83	5.7	.66	1.36	560	3
12.7	3.55	2.36	21.5	106	1.7	1.2	.17	.84	5	.78	1.29	600	3
12.51	1.24	2.25	17.5	85	2	.58	.6	1.25	5.45	.75	1.51	650	3

       酒的品种可能属于3种类别。表2展示了wine数据集的部分样本情况。所以，本文的目的就是运用分类算法，挑选相应的特征属性来构造相应的决策树，挖掘wine数据集类别与13个特征之间的关系。并利用所构造的决策树来对测试样本做预测，分析预测误差，从而证明所构造的决策树的合理性。

2、C4.5算法对UCI wine数据集分类的实现

2.1、C4.5算法分类流程设计

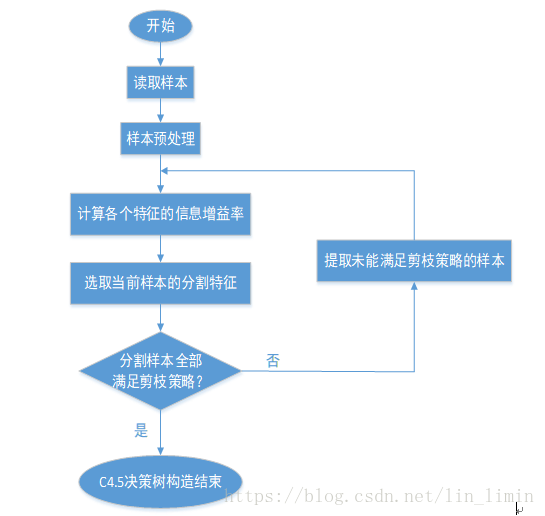
图1 C4.5算法构造决策树流程设计 

       C4.5算法是决策树分类领域的一种较为经典的算法，图1展示了本次使用C4.5算法构造决策树的算法流程。

       首先，从UCI 机器学习库上下载wine数据集，提取样本。这里将所有样本分为训练样本和测试样本两部分。训练样本用来训练C4.5算法，测试样本用来最后测试C4.5算法所构造的决策树的正确性。所以样本预处理部分便是将训练样本与测试样本分开。本文采用的是随机采样的方法来分开训练样本和测试样本。

       然后，将随机采样所得到的训练样本用来构造决策树。依次对训练样本的各个特征计算信息增益率，选择具有最大信息增益率的特征作为当前样本的分割特征，对决策树进行分支。

       如果决策树分支之后，所有的分割样本都满足预先定义的决策树剪枝策略，则完成对训练样本构造决策树的目标。否则将利用分割样本递归构造决策树，直到所有的分割样本都满足剪枝策略为止。

 

图2 测试样本类别预测流程图

       C4.5算法构造决策树后，需要对决策树的合理性做评估。图2展示了利用所构造的决策树预测测试样本类别流程。通过对决策树的预测误差作分析，来判别所构造的决策树是否可行。下面将介绍具体的决策树构造过程。

2.2、C4.5算法构造决策树

2.2.1 树节点设计

图3 决策树节点设计

      图3显示了决策树节点的所有成员属性。Feature_tosplit用来记录当前节点的分割特征，location记录分割特征的分割界限，value表征的是属于当前节点的特征的取值情况，而child描述按照feature_tosplit和location进行分支后，隶属于当前节点的子节点。需要注意的是，如果当前节点已经是叶子节点，则利用child属性来记录当前节点的标签，相应地，将feature_tosplit设置为0，将location和value设置为空。

2.2.2 特征取值连续处理

       当属性类型为离散型，无须对数据进行离散化处理；而当属性类型为连续型时，则需要对数据进行离散化处理。为此，节点分裂之前先要对属性的类型做判断。

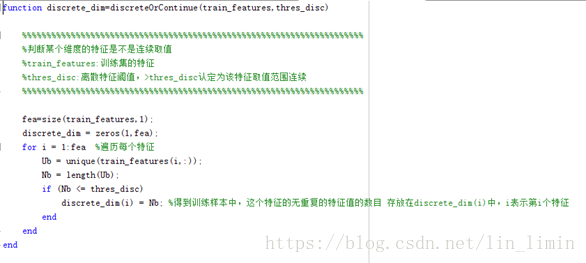
图4 属性类型判断 

       图4是对某一维度属性类型判断的相关代码。Thres_disc是为了判断属性是离散类型还是连续类型而设立的一个阈值，在算法的运行过程中，设定thres_disc=10。当某一维度属性的所有可能取值情况多于thres_disc时，认为该属性的类型是离散型；否则认为是连续型。

       对于连续型的属性，本文利用C4.5算法离散化的核心思想是：将属性A（假设属性A是连续取值）的N个属性值按升序排列；通过二分法将属性A的所有属性值分成两部分（共有N-1种划分方法，二分的阈值为相邻两个属性值的中间值）；计算每种划分方法对应的信息增益，选取信息增益最大的划分方法的阈值作为属性A二分的阈值。

       详细流程如下：

       1）将节点Node上的所有数据样本按照连续型属性A的具体取值，由小到大进行排列，得到属性A的属性值取值序列；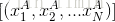

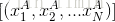
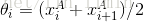
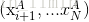
       2）在序列中共有N-1种二分方法，即共产生N-1个分隔阈值。对于第i种二分方法，其二分阈值 。它将该节点上的数据集划分为2个子数据集和 。计算此种二分结果下的信息增益。

       3）分别计算N-1种二分结果下的信息增益率，选取信息增益率最大的二分结果作为对属性A的划分结果，并记录此时的二分阈值。

 

图5 连续属性离散化处理及相应信息增益率的计算 

       图5是对连续属性离散化处理的相关代码。对N-1个可能的分割点分别计算信息增益率将耗费很多计算时间，大大提高了算法的时间复杂度。对于这一点，后文的4.3小节还会做进一步的讨论。

2.2.3 剪枝策略

       由于决策树的建立完全是依赖于训练样本，因此决策树对训练样本能够产生完美的拟合效果。但这样的决策树对于测试样本来说过于庞大而复杂，可能产生较高的分类错误率。这种现象就称为过拟合。因此需要将复杂的决策树进行简化，即去掉一些节点解决过拟合问题。

      本文在防止决策树出现过拟合的问题上采用的是预剪枝的方法：定义一个阈值(pruning)，当达到某个节点的实例个数小于阈值时就可以停止决策树的生长。

图6 剪枝阈值的设定

       对于剪枝阈值(pruning)的设定，使其与训练样本的个数成正比，而不是设定成一个固定的值，这样可以方便地处理各种容量的样本数据。

 

图7 剪枝阈值用于控制决策树的构造

      最后将剪枝阈值用于控制决策树的生长：当剩余的训练样本数太少时，不让当前节点继续分裂，并将剩余训练样本所属类别最多的类别作为当前节点的最终标签。

2.2.4  决策树构造结果

 

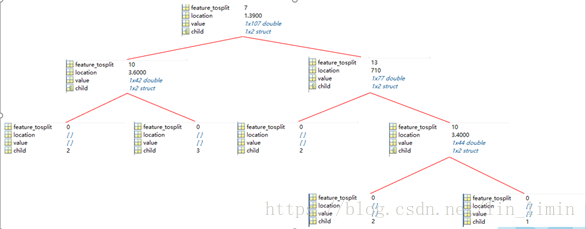
图8 C4.5算法所构造决策树结构及节点属性 

      按照前文所描述的C4.5算法构造决策树的相关操作，并利用MATLAB编程实现对wine数据集的决策树构造，最终得到如图8所示的决策树结构。各个节点的属性所代表的含义如2.2.1小节所述。

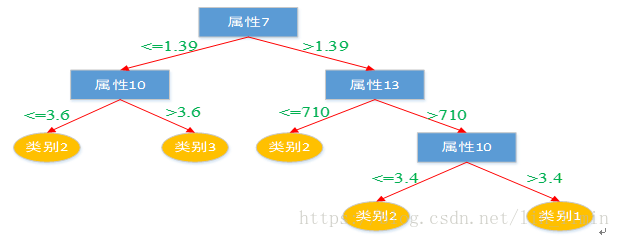
图9 C4.5算法所构造决策树

      将图8所示结构转化为图9更为明了的决策树示意图。下面将对所构造的决策树的合理性进行评估。

2.3、C4.5算法的分类准确度

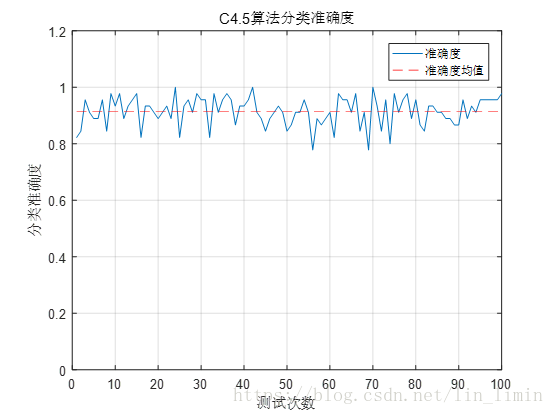
图10 C4.5算法分类准确度分析 

       把随机采样之后剩余的部分样本作为测试样本，利用图9所示的决策树对测试样本做预测，来评估C4.5算法构造决策树的分类准确度。

       图10是用MATLAB运行100次的实验结果。在这100次的测试中，基本上决策树的预测准确度均在80%以上，预测的准确度均值约为92%，已经能够提取大部分的有效特征来对wine做分类，实现了基本的分类需求。

3、C4.5算法与CART算法的比较

      本文着重实现了C4.5决策树算法对于wine训练集的分类，也在第2节中用了大量篇幅讲解了具体的实现细节。但是提到决策树算法，又不得不提及CART算法。故本节将对比C4.5算法和CART算法在wine数据集的训练效果，但对于CART算法的具体细节将不再过多阐述，网上有很多很优秀的讲解。

图11 CART算法所构造决策树 

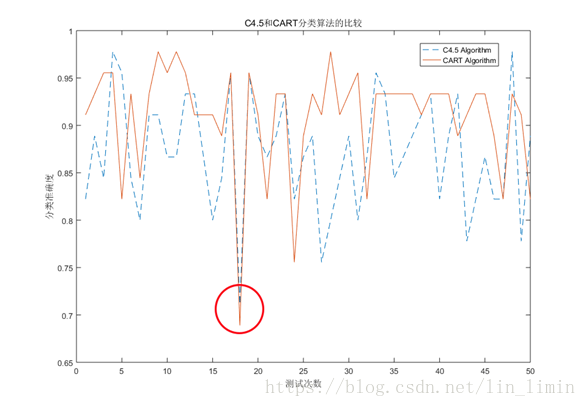
图12 C4.5和CART算法的分类准确度比较 

       图11呈现了利用CART算法最终所构造的决策树。与图9 C4.5算法的决策树结构存在差异。但两者在分割特征的选取上有很大的相似性，比如都充分利用了属性7，属性10以及属性13来构造决策树。

       图12是50次实验下，利用图9和图11对测试数据的分类准确度比较。需要注意的是，每次实验，两种算法运用的训练集和测试集虽然都是随机采样的得到的，但是两者的数据是完全相同的。否则对于两种算法的准确度比较将没有意义。

       总体而言，CART决策树的分类准确度会高于C4.5所构造的决策树。原因可能在于本文采样的预剪枝的剪枝策略有待改进，剪枝阈值的设定可能不是最优从而导致C4.5决策树过早地停止生长。如果以后要进一步地优化本文的C4.5决策树分类策略，可以从这点出发对剪枝策略进行改进。

4、实验分析与讨论

4.1 准确度问题

       首先分析的是，某些测试条件下，分类准确度异常的现象。

 

图13 准确度异常现象 

      再次考虑图12两种分类算法的准确度对比结果。可以发现，虽然大多数情况下两种算法的预测准确度可以达到85%甚至更高，但是也存在着某些点准确度很低的情况。正如图13红色圆圈所圈出来的点。

图14 采样不均匀样本

 

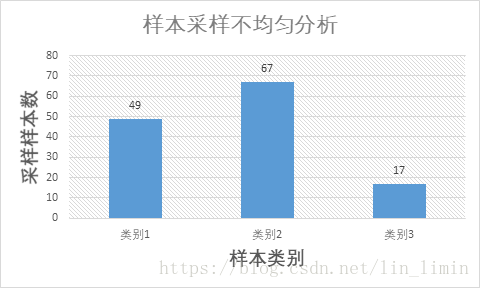
图15 样本采样不均匀分析 

      最终发现问题出在随机采样。本文之所以采用随机采样的方法，是因为这样训练出来的决策树更具有普适性：它可以减少人工分离训练样本和测试样本所带来的训练误差。

       但是随机采样也有可能带来新的问题。正如图14和图15所示，采样训练样本的时候可能存在采样不均匀的现象：某些类别的训练样本数有可能很低。这样一来，就很难找到相应的特征对这一类别的样本做分类，随之就有可能出现图13所示某些情况决策树分类准确度较低的现象。

       随机采样的优越性很明显，如果每次训练都固定训练样本，则有可能训练出来的决策树只适合当前样本而不具备实用性。但同时也要考虑随机采样带来的新问题。一个解决办法就是多进行几次训练，训练之后准确度分析取平均或者剔除异常数据，减少采样不均匀带来的影响。

4.2、缺省值问题

       在本文利用C4.5算法对UCI wine数据集分类过程中，并未出现特征缺少特征值的现象。但是现实中的数据却往往可能因为保存不周等原因造成数据集某些特征值的缺失。特征参数的缺失不仅影响模型的训练，还会影响我们利用模型进行样本预测。本小节对缺省值问题进行讨论。

      对于缺省值处理的问题，主要需要解决的是两个问题：一是在样本某些特征缺失的情况下选择划分的属性；二是选定了划分属性，对于在该属性上缺失特征的样本的处理。

      对于第一个子问题，假设现有缺失特征值的特征A。解决思路可以将数据分成两部分，对每个样本设置一个权重（初始值设为1），然后划分数据，一部分是有特征值A的数据D1，另一部分是没有特征A的数据D2。然后对于没有缺失特征A的数据集D1计算A特征的信息增益率，最后乘上一个系数η，η等于特征A无缺失的样本占总样本的比例。

      对于第二个子问题，可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1，A2，A3。3个特征值对应的无缺失A特征的样本个数为2，3，4。则a同时划分入A1，A2，A3，对应权重调节为2/9，3/9，4/9。接着递归构造决策树直到决策树构造完成。

4.3、 算法复杂性问题

       在C4.5构造决策树的过程中，节点的分割属性的选择至关重要。C4.5算法使用的是信息增益率作为特征的分割标准。然而信息增益率的计算较为复杂，这一点在对连续属性的处理上被进一步地凸现出来。

图16 算法运行时间分析 

      图16展示了C4.5算法和CART算法在处理本文选择的wine数据集的程序运行时间的对比。其中，程序的运行时间可以通过调用MATLAB的tic和toc做差得到。图16的小图对应的是CART算法运行时间的局部放大图。

       从中可以明显看出，C4.5算法的运行时间远远大于CART算法的执行时间，这一差距随着样本容量的变大将被进一步的拉大。

       为了更为高效地建立决策树用于分类，可以从运用简化的二叉树模型替代多叉树模型和用近似的基尼系数来取代信息增益率来简化计算两方面着手。减少算法的执行时间。

5、总结

       本文是数据挖掘课程中的一份大作业的实现。如有错误之处，望指正。完整代码可从这里下载：C4.5 决策树算法对UCI wine数据集分类的实现(MATLAB)。

6、代码附录

6.1、wine.m（可执行文件）

clear;
clc;
% traindata = textread('TrainData.txt');  
% testdata = textread('TestData.txt');
winedata=textread('WineData.txt');runtime=100;
for i=1:runtime%     tic;%用于计算程序运行时间train_index=randperm(length(winedata),floor(length(winedata)/4*3));%随机采样，3/4数据作为训练样本，其余的作为测试样本test_index=setdiff(linspace(1,length(winedata),length(winedata)),train_index);traindata=winedata(train_index,:);%训练样本testdata=winedata(test_index,:);%测试样本train_features=traindata(:,2:(size(traindata,2)));  train_targets=traindata(:,1)';  test_features=testdata(:,2:(size(testdata,2)));  test_targets=testdata(:,1)';test_targets_predict1 = C4_5(train_features', train_targets, test_features'); %调用C4.5算法用于分类%test_targets_predict = C4_5(train_features', train_targets, test_features', 5, 10);t=classregtree(train_features,train_targets');%调用CART算法用于分类test_targets_predict2=eval(t,test_features);%train_features'行是feature，列是样本  %train_targets 是1行多列，列是训练样本个数  % test_features'行是feature，列是样本 %计算决策树预测的准确度accuracy(i,1)=cal_accuracy(test_targets,test_targets_predict1);accuracy(i,2)=cal_accuracy(test_targets,test_targets_predict2');%    t1(i)=toc;
%    save t1.mat t1;
end  % plot(accuracy(:,1));
% hold on;
% plot(repmat(mean(accuracy(:,1)),length(accuracy(:,1)),1),'r--');
% legend('准确度','准确度均值');
% title('C4.5算法分类准确度');
% xlabel('测试次数');
% ylabel('分类准确度');
% ylim([0,1.2]);
% grid;plot(accuracy(:,1),'--');
hold on;
plot(accuracy(:,2));
legend('C4.5 Algorithm','CART Algorithm');
xlabel('测试次数');
ylabel('分类准确度');
title('C4.5和CART分类算法的比较');
%ylim([0,1.2]);
grid;

6.2、C4.5.m

function test_targets = improved_C4_5(train_features, train_targets, test_features,varargin)    pruning=35;
thres_disc=10;
if nargin>4pruning=varargin{1};thres_disc=varargin{2};
elseif nargin>3thres_disc=varargin{1};
end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%training_features：训练样本的特征  
%training_targets：训练样本所属类别  
%test_features：测试样本的特征   
%pruning：剪枝系数  
%thres_disc:离散特征阈值，>thres_disc认定为该特征取值范围连续 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%[fea, num]     = size(train_features); %num是训练样本数，fea是特征数目  pruning    = pruning*num/100;  % 用于剪枝 %判断某一维的特征是离散取值还是连续取值，0代表是连续特征discrete_dim =discreteOrContinue(train_features,thres_disc); % 递归地构造树  %disp('Building tree')    tree= build_tree(train_features, train_targets,discrete_dim,0,pruning);    save tree.mat tree;  %加入悲观剪枝的操作  %在完全生长的决策树的基础上，对生长后分类效果不佳的子树进行修剪，减小决策树的复杂度，降低过拟合的影响  %treeplot(tree);  %样本预测    %disp('Classify test samples using the tree')    test_targets= predict(tree,test_features, 1:size(test_features,2), discrete_dim);    

6.3、discreteOrContinue.m（离散连续属性判断）

function discrete_dim=discreteOrContinue(train_features,thres_disc)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%判断某个维度的特征是不是连续取值%train_features:训练集的特征%thres_disc:离散特征阈值，>thres_disc认定为该特征取值范围连续%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%fea=size(train_features,1);discrete_dim = zeros(1,fea);for i = 1:fea  %遍历每个特征  Ub = unique(train_features(i,:)); Nb = length(Ub);   if (Nb <= thres_disc)    discrete_dim(i) = Nb; %得到训练样本中，这个特征的无重复的特征值的数目 存放在discrete_dim(i)中，i表示第i个特征  end    end
end

6.4、build_tree.m（C4.5算法建树）

function tree = build_tree(train_features, train_targets, discrete_dim, layer,varargin)    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%调用C4.5决策树算法建立决策树
%training_features：训练样本的特征  
%training_targets：训练样本所属类别  
%discrete_dim：各个维度的特征是否是连续特征，0指的是连续特征  
%layer:节点所属树的层数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%if nargin>5pruning=varargin{1};
elsepruning=35;
end[fea, L]= size(train_features);  
ale= unique(train_targets);  
tree.feature_tosplit= 0;  
tree.location=inf;  %初始化分裂位置是inf  if isempty(train_features)   return    
end    if ((pruning > L) || (L == 1) ||(length(ale) == 1)) %如果剩余训练样本太小(小于pruning)，或只剩一个，或只剩一类标签，退出    his= hist(train_targets, length(ale));  %统计样本的标签，分别属于每个标签的数目  [num, largest]= max(his); tree.value= [];    tree.location  = [];    tree.child= ale(largest);return    
end    for i = 1:length(ale) %遍历判别标签的数目   Pnode(i) = length(find(train_targets == ale(i))) / L; 
end   %计算当前节点的信息熵 
Inode = -sum(Pnode.*log2(Pnode));    el= zeros(1, fea);  %记录每个特征的信息增益率  
location= ones(1, fea)*inf;for i = 1:fea %遍历每个特征    data= train_features(i,:); pe= unique(data);    nu= length(pe);   if (discrete_dim(i)) %离散特征   node= zeros(length(ale), nu);for j = 1:length(ale) %遍历每个标签    for k = 1:nu %遍历每个特征值    indices     = find((train_targets == ale(j)) && (train_features(i,:) == pe(k)));    node(j,k)  = length(indices);end    end    rocle= sum(node);P1= repmat(rocle, length(ale), 1);P1= P1 + eps*(P1==0);node= node./P1;rocle= rocle/sum(rocle);info= sum(-node.*log(eps+node)/log(2));  %每个特征分别计算信息熵,eps是为了防止对数为1 el(i) = (Inode-sum(rocle.*info))/(-sum(rocle.*log(eps+rocle)/log(2))); %信息增益率   else   %连续特征node= zeros(length(ale), 2);[sorted_data, indices] = sort(data);sorted_targets = train_targets(indices);%计算分裂信息度量  I = zeros(1,nu);  spl= zeros(1, nu);  for j = 1:nu-1  %特征i有Nbins个连续值，设定Nbins-1个可能的分割点，对每个分割点计算信息增益率node(:, 1) = hist(sorted_targets(find(sorted_data <= pe(j))) , ale);  node(:, 2) = hist(sorted_targets(find(sorted_data > pe(j))) , ale);   Ps= sum(node)/L; node= node/L; rocle= sum(node);    P1= repmat(rocle, length(ale), 1); P1= P1 + eps*(P1==0);    info= sum(-node./P1.*log(eps+node./P1)/log(2)); %信息增益I(j)= Inode - sum(info.*Ps);   spl(j) =I(j)/(-sum(Ps.*log(eps+Ps)/log(2)));  %第j个分割点的信息增益率end  [~, s] = max(I);  %求所有分割点的最大信息增益率el(i) = spl(s);  location(i) = pe(s);  %对应特征i的划分位置就是能使信息增益最大的划分值  end    
end    %找到当前要作为分裂特征的特征  
[num, feature_tosplit]= max(el); 
dims= 1:fea;  %特征数目  
tree.feature_tosplit= feature_tosplit;  %记为树的分裂特征  value= unique(train_features(feature_tosplit,:)); 
nu= length(value);
tree.value = value;  %记为树的分类特征向量 当前所有样本的这个特征的特征值  
tree.location = location(feature_tosplit);  %树的分裂位置if (nu == 1)  %无重复的特征值的数目==1，即这个特征只有这一个特征值，就不能进行分裂  his= hist(train_targets, length(ale));[num, largest]= max(his); tree.value= [];tree.location  = [];    tree.child= ale(largest); return    
end    if (discrete_dim(feature_tosplit))  %如果当前选择的这个作为分裂特征的特征是个离散特征   for i = 1:nu   %遍历这个特征下无重复的特征值的数目  indices= find(train_features(feature_tosplit, :) == value(i));tree.child(i)= build_tree(train_features(dims, indices), train_targets(indices), discrete_dim(dims), layer, pruning);%递归  %离散特征，分叉成Nbins个，分别针对每个特征值里的样本，进行再分叉  end    
else%如果当前选择的这个作为分裂特征的特征是个连续特征
indices1= find(train_features(feature_tosplit,:) <= location(feature_tosplit));  %找到特征值<=分裂值的样本的索引们  
indices2= find(train_features(feature_tosplit,:) > location(feature_tosplit));if ~(isempty(indices1) || isempty(indices2))  %如果<=分裂值 >分裂值的样本数目都不等于0    tree.child(1)= build_tree(train_features(dims, indices1), train_targets(indices1), discrete_dim(dims),layer+1, pruning);tree.child(2)= build_tree(train_features(dims, indices2), train_targets(indices2), discrete_dim(dims),layer+1, pruning);   else    his= hist(train_targets, length(ale));  %统计当前所有样本的标签，分别属于每个标签的数目 [num, largest]= max(his);tree.child= ale(largest);   tree.feature_tosplit= 0;  %树的分裂特征记为0  end    
end 

6.5、predict.m（按照建立的决策树对测试样本做预测）

function targets = predict(tree,test_features, indices, discrete_dim)       %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%调用C4.5决策树算法对测试样本进行预测
%tree：C4.5算法所建立的决策树 
%test_features：测试样本的特征 
%indices：索引 
%discrete:各个维度的特征是否是连续取值，0指的是连续取值
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%targets = zeros(1, size(test_features,2)); if (tree.feature_tosplit == 0)  targets(indices) = tree.child;  %得到样本对应的标签是tree.child  return    
end    feature_tosplit = tree.feature_tosplit;  %得到分裂特征  
dims= 1:size(test_features,1);  %得到特征索引  % 根据得到的决策树对测试样本进行分类  
if (discrete_dim(feature_tosplit) == 0) %如果当前分裂特征是个连续特征 in= indices(find(test_features(feature_tosplit, indices)<= tree.location));  targets= targets + predict( tree.child(1),test_features(dims, :), in,discrete_dim(dims)); in= indices(find(test_features(feature_tosplit, indices)>tree.location)); targets= targets + predict(tree.child(2),test_features(dims, :),in,discrete_dim(dims));   
else  %如果当前分裂特征是个离散特征  Uf= unique(test_features(feature_tosplit,:)); %得到这个样本集中这个特征的无重复特征值  for i = 1:length(Uf)  %遍历每个特征值    if any(Uf(i) == tree.value)  %tree.Nf为树的分类特征向量 当前所有样本的这个特征的特征值  in= indices(find(test_features(feature_tosplit, indices) == Uf(i)));  %找到当前测试样本中这个特征的特征值==分裂值的样本索引  targets = targets + predict(tree.child(find(Uf(i)==tree.value)),test_features(dims, :),in,discrete_dim(dims));%对这部分样本再分叉   end    end    
end 

6.6、cal_accuracy.m（按照建立的决策树对测试样本做预测）

function accuracy=cal_accuracy(test_targets,test_targets_predict)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%计算决策树分类算法的准确度%test_targets:测试数据集的实际所属类别%test_targets_predict:决策树算法所预测的测试数据集的所属类别%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%right=0;for j=1:size(test_targets_predict,2)  if test_targets(:,j)==test_targets_predict(:,j)  right=right+1;  end  endaccuracy=right/size(test_targets,2);
end

6.7、WineData.txt（UCI 数据集，记得与wine.m放置到同一文件夹下）

1 14.23 1.71 2.43 15.6 127 2.8 3.06 .28 2.29 5.64 1.04 3.92 1065
1 13.2  1.78 2.14 11.2 100 2.65 2.76 .26 1.28 4.38 1.05 3.4 1050
1 13.16  2.36 2.67 18.6 101 2.8 3.24 .3 2.81 5.68 1.03 3.17 1185
1 14.37  1.95 2.5  16.8 113 3.85 3.49 .24 2.18 7.8 .86 3.45 1480
1 13.24  2.59 2.87 21   118 2.8 2.69 .39 1.82 4.32 1.04 2.93 735
1 14.2 1.76 2.45 15.2 112 3.27 3.39 .34 1.97 6.75 1.05 2.85 1450
1 14.39   1.87 2.45 14.6 96 2.5 2.52 .3 1.98 5.25 1.02 3.58 1290
1 14.06 2.15 2.61 17.6 121 2.6 2.51 .31 1.25 5.05 1.06 3.58 1295
1 14.83     1.64 2.17 14 97 2.8 2.98 .29 1.98 5.2 1.08 2.85 1045
1 13.86   1.35 2.27 16 98 2.98 3.15 .22 1.85 7.22 1.01 3.55 1045
1 14.1 2.16 2.3 18 105    2.95 3.32 .22 2.38 5.75 1.25 3.17 1510
1 14.12 1.48 2.32     16.8 95 2.2 2.43 .26 1.57 5 1.17 2.82 1280
1 13.75 1.73 2.41 16  89 2.6     2.76 .29 1.81 5.6 1.15 2.9 1320
1 14.75 1.73 2.39   11.4 91 3.1 3.69 .43 2.81 5.4 1.25 2.73 1150
1 14.38   1.87  2.38   12 102 3.3   3.64 .29 2.96 7.5 1.2 3 1547
1 13.63  1.81 2.7 17.2  112 2.85 2.91 .3 1.46 7.3 1.28 2.88 1310
1 14.3 1.92 2.72   20 120   2.8 3.14 .33 1.97 6.2 1.07 2.65 1280
1 13.83  1.57  2.62 20   115 2.95 3.4 .4 1.72 6.6 1.13 2.57 1130
1 14.19  1.59 2.48 16.5 108 3.3 3.93 .32 1.86 8.7 1.23 2.82 1680
1 13.64 3.1   2.56 15.2   116 2.7 3.03 .17 1.66 5.1 .96 3.36 845
1 14.06  1.63   2.28 16   126 3 3.17 .24 2.1 5.65  1.09 3.71 780
1 12.93 3.8 2.65 18.6 102 2.41 2.41 .25   1.98 4.5 1.03 3.52 770
1 13.71 1.86 2.36 16.6  101 2.61 2.88 .27   1.69 3.8 1.11 4 1035
1 12.85  1.6 2.52 17.8 95 2.48 2.37 .26 1.46 3.93 1.09 3.63 1015
1 13.5   1.81 2.61   20 96 2.53 2.61 .28 1.66 3.52 1.12 3.82 845
1 13.05  2.05 3.22   25 124 2.63 2.68 .47 1.92 3.58 1.13 3.2 830
1 13.39 1.77 2.62 16.1 93 2.85   2.94 .34 1.45 4.8 .92 3.22 1195
1 13.3 1.72 2.14 17 94   2.4 2.19 .27   1.35 3.95 1.02 2.77 1285
1 13.87 1.9 2.8 19.4  107 2.95  2.97 .37   1.76 4.5 1.25 3.4 915
1 14.02    1.68 2.21 16 96 2.65 2.33 .26 1.98 4.7 1.04 3.59 1035
1 13.73   1.5 2.7   22.5 101  3 3.25 .29 2.38 5.7 1.19 2.71 1285
1 13.58 1.66 2.36 19.1 106 2.86 3.19 .22 1.95 6.9 1.09 2.88 1515
1 13.68 1.83 2.36 17.2 104 2.42 2.69 .42 1.97 3.84 1.23 2.87 990
1 13.76   1.53 2.7 19.5 132 2.95    2.74 .5 1.35 5.4 1.25 3 1235
1 13.51 1.8    2.65 19  110 2.35 2.53 .29 1.54 4.2 1.1 2.87 1095
1 13.48 1.81 2.41 20.5 100   2.7 2.98 .26 1.86 5.1 1.04 3.47 920
1 13.28   1.64 2.84 15.5 110 2.6 2.68 .34 1.36 4.6 1.09 2.78 880
1 13.05 1.65   2.55 18 98 2.45 2.43 .29 1.44 4.25 1.12 2.51 1105
1 13.07    1.5 2.1 15.5  98 2.4 2.64 .28 1.37 3.7 1.18 2.69 1020
1 14.22 3.99    2.51 13.2    128 3 3.04 .2 2.08 5.1 .89 3.53 760
1 13.56  1.71 2.31 16.2 117 3.15 3.29 .34 2.34 6.13 .95 3.38 795
1 13.41   3.84  2.12  18.8 90 2.45 2.68 .27 1.48 4.28 .91 3 1035
1 13.88 1.89   2.59 15  101 3.25 3.56 .17 1.7 5.43 .88 3.56 1095
1 13.24 3.98   2.29 17.5   103 2.64 2.63 .32 1.66 4.36 .82 3 680
1 13.05 1.77 2.1 17   107 3 3   .28   2.03   5.04   .88 3.35 885
1 14.21 4.04 2.44  18.9 111 2.85 2.65 .3 1.25 5.24 .87 3.33 1080
1 14.38 3.59 2.28 16   102 3.25 3.17 .27 2.19 4.9 1.04 3.44 1065
1 13.9 1.68 2.12 16  101 3.1  3.39 .21   2.14  6.1  .91 3.33 985
1 14.1 2.02 2.4 18.8 103  2.75  2.92 .32 2.38 6.2 1.07 2.75 1060
1 13.94 1.73 2.27 17.4 108 2.88 3.54 .32 2.08 8.90 1.12 3.1 1260
1 13.05 1.73 2.04 12.4 92 2.72 3.27  .17 2.91 7.2 1.12 2.91 1150
1 13.83 1.65 2.6 17.2 94 2.45 2.99   .22 2.29 5.6 1.24 3.37 1265
1 13.82 1.75 2.42 14 111 3.88 3.74  .32 1.87 7.05 1.01 3.26 1190
1 13.77 1.9 2.68   17.1 115 3  2.79 .39  1.68 6.3 1.13 2.93 1375
1 13.74 1.67 2.25 16.4 118 2.6 2.9  .21 1.62 5.85 .92   3.2 1060
1 13.56 1.73 2.46 20.5 116 2.96 2.78  .2 2.45 6.25 .98 3.03 1120
1 14.22 1.7 2.3 16.3  118    3.2 3    .26 2.03 6.38 .94 3.31 970
1 13.29 1.97 2.68 16.8 102 3   3.23    .31 1.66 6 1.07 2.84 1270
1 13.72 1.43 2.5 16.7  108 3.4   3.67 .19 2.04 6.8 .89 2.87 1285
2 12.37 .94  1.36 10.6 88    1.98 .57 .28 .42 1.95 1.05 1.82 520
2 12.33 1.1  2.28 16 101    2.05 1.09 .63 .41 3.27 1.25 1.67 680
2 12.64 1.36 2.02 16.8 100   2.02 1.41 .53 .62 5.75 .98 1.59 450
2 13.67 1.25   1.92 18     94 2.1 1.79 .32 .73 3.8 1.23 2.46 630
2 12.37   1.13 2.16    19 87 3.5 3.1 .19 1.87 4.45 1.22 2.87 420
2 12.17 1.45   2.53 19 104 1.89 1.75 .45 1.03 2.95 1.45 2.23 355
2 12.37    1.21 2.56 18.1 98 2.42 2.65 .37 2.08 4.6 1.19 2.3 678
2 13.11  1.01    1.7 15 78 2.98  3.18 .26 2.28 5.3 1.12 3.18 502
2 12.37 1.17 1.92  19.6 78    2.11 2 .27 1.04 4.68 1.12 3.48 510
2 13.34  .94   2.36 17   110 2.53 1.3 .55 .42 3.17 1.02 1.93 750
2 12.21  1.19 1.75 16.8 151 1.85 1.28 .14 2.5 2.85 1.28 3.07 718
2 12.29  1.61 2.21 20.4 103 1.1 1.02 .37 1.46 3.05 .906 1.82 870
2 13.86  1.51   2.67 25 86 2.95 2.86 .21 1.87 3.38 1.36 3.16 410
2 13.49  1.66    2.24 24 87 1.88 1.84 .27 1.03 3.74 .98 2.78 472
2 12.99 1.67    2.6 30 139   3.3 2.89 .21 1.96 3.35 1.31 3.5 985
2 11.96 1.09  2.3 21 101    3.38 2.14 .13 1.65 3.21 .99 3.13 886
2 11.66 1.88  1.92    16 97 1.61 1.57 .34 1.15 3.8 1.23 2.14 428
2 13.03 .9    1.71    16 86 1.95 2.03 .24 1.46 4.6 1.19 2.48 392
2 11.84 2.89  2.23 18    112 1.72 1.32 .43 .95 2.65 .96 2.52 500
2 12.33 .99    1.95 14.8 136 1.9 1.85 .35 2.76 3.4 1.06 2.31 750
2 12.7 3.87  2.4    23 101 2.83 2.55 .43 1.95 2.57 1.19 3.13 463
2 12 .92    2 19    86 2.42    2.26    .3 1.43 2.5 1.38 3.12 278
2 12.72    1.81  2.2 18.8 86 2.2 2.53 .26 1.77 3.9 1.16 3.14 714
2 12.08 1.13    2.51 24    78 2    1.58 .4 1.4 2.2 1.31 2.72 630
2 13.05 3.86 2.32    22.5 85 1.65 1.59 .61 1.62 4.8 .84 2.01 515
2 11.84 .89 2.58    18 94    2.2 2.21 .22 2.35 3.05 .79 3.08 520
2 12.67    .98 2.24    18 99 2.2 1.94 .3 1.46 2.62 1.23 3.16 450
2 12.16  1.61 2.31 22.8 90 1.78 1.69 .43 1.56 2.45 1.33 2.26 495
2 11.65 1.67    2.62   26 88 1.92 1.61 .4 1.34 2.6 1.36 3.21 562
2 11.64   2.06 2.46    21.6 84 1.95 1.69 .48 1.35 2.8 1 2.75 680
2 12.08   1.33  2.3 23.6 70 2.2 1.59 .42 1.38 1.74 1.07 3.21 625
2 12.08 1.83    2.32  18.5 81 1.6 1.5 .52 1.64 2.4 1.08 2.27 480
2 12   1.51    2.42 22 86    1.45 1.25 .5 1.63 3.6 1.05 2.65 450
2 12.69   1.53 2.26 20.7 80 1.38 1.46 .58 1.62 3.05 .96 2.06 495
2 12.29 2.83    2.22  18 88 2.45 2.25 .25 1.99 2.15 1.15 3.3 290
2 11.62    1.99 2.28 18 98 3.02 2.26 .17 1.35 3.25 1.16 2.96 345
2 12.47 1.52 2.2    19 162   2.5 2.27 .32 3.28 2.6 1.16 2.63 937
2 11.81 2.12 2.74  21.5 134    1.6 .99 .14 1.56 2.5 .95 2.26 625
2 12.29 1.41   1.98 16 85    2.55 2.5 .29 1.77 2.9 1.23 2.74 428
2 12.37 1.07    2.1 18.5 88 3.52 3.75 .24 1.95 4.5 1.04 2.77 660
2 12.29    3.17  2.21 18 88 2.85 2.99 .45 2.81 2.3 1.42 2.83 406
2 12.08 2.08 1.7 17.5 97   2.23   2.17 .26 1.4 3.3 1.27 2.96 710
2 12.6 1.34 1.9 18.5 88 1.45  1.36   .29 1.35 2.45 1.04 2.77 562
2 12.34 2.45 2.46 21 98   2.56   2.11   .34 1.31 2.8 .8 3.38 438
2 11.82 1.72 1.88 19.5 86   2.5 1.64  .37 1.42 2.06 .94 2.44 415
2 12.51 1.73 1.98 20.5 85 2.2 1.92 .32   1.48 2.94 1.04 3.57 672
2 12.42 2.55 2.27 22 90   1.68   1.84   .66 1.42 2.7 .86 3.3 315
2 12.25 1.73 2.12 19 80 1.65    2.03 .37    1.63  3.4 1 3.17 510
2 12.72 1.75 2.28 22.5 84 1.38 1.76 .48 1.63    3.3 .88 2.42 488
2 12.22 1.29 1.94 19 92 2.36 2.04   .39    2.08 2.7 .86 3.02 312
2 11.61 1.35 2.7 20 94 2.74 2.92    .29 2.49   2.65 .96 3.26 680
2 11.46 3.74 1.82 19.5 107 3.18 2.58 .24   3.58 2.9 .75 2.81 562
2 12.52 2.43 2.17 21 88   2.55   2.27   .26 1.22   2 .9 2.78 325
2 11.76 2.68 2.92 20 103 1.75 2.03    .6   1.05 3.8 1.23 2.5 607
2 11.41 .74 2.5 21 88 2.48 2.01    .42 1.44    3.08 1.1 2.31 434
2 12.08 1.39 2.5 22.5 84 2.56 2.29 .43 1.04    2.9 .93  3.19 385
2 11.03 1.51 2.2 21.5 85 2.46 2.17 .52 2.01 1.9    1.71 2.87 407
2 11.82 1.47 1.99 20.8 86 1.98 1.6 .3  1.53    1.95 .95 3.33 495
2 12.42 1.61 2.19 22.5 108 2 2.09 .34    1.61 2.06 1.06 2.96 345
2 12.77 3.43 1.98  16 80    1.63    1.25 .43 .83 3.4 .7 2.12 372
2 12 3.43 2 19 87    2 1.64    .37    1.87    1.28  .93 3.05 564
2 11.45 2.4 2.42 20 96 2.9 2.79  .32    1.83 3.25    .8 3.39 625
2 11.56 2.05 3.23 28.5 119  3.18    5.08 .47 1.87 6 .93 3.69 465
2 12.42 4.43 2.73 26.5 102 2.2   2.13 .43 1.71 2.08 .92 3.12 365
2 13.05 5.8 2.13 21.5 86 2.62    2.65 .3    2.01 2.6 .73 3.1 380
2 11.87 4.31 2.39 21 82 2.86 3.03 .21   2.91    2.8 .75 3.64 380
2 12.07 2.16 2.17 21 85 2.6   2.65    .37 1.35 2.76 .86 3.28 378
2 12.43 1.53 2.29 21.5 86   2.74 3.15 .39 1.77 3.94 .69 2.84 352
2 11.79 2.13 2.78 28.5    92   2.13 2.24 .58 1.76 3 .97 2.44 466
2 12.37 1.63 2.3 24.5 88 2.22    2.45   .4 1.9 2.12 .89 2.78 342
2 12.04 4.3 2.38 22 80 2.1   1.75   .42    1.35 2.6 .79 2.57 580
3 12.86 1.35   2.32    18 122 1.51 1.25 .21 .94 4.1 .76 1.29 630
3 12.88   2.99   2.4 20    104 1.3 1.22 .24 .83 5.4 .74 1.42 530
3 12.81 2.31   2.4 24    98   1.15 1.09 .27 .83 5.7 .66 1.36 560
3 12.7  3.55   2.36    21.5 106   1.7 1.2 .17 .84 5 .78 1.29 600
3 12.51    1.24 2.25   17.5 85 2   .58 .6 1.25 5.45 .75 1.51 650
3 12.6 2.46  2.2 18.5 94    1.62 .66    .63 .94 7.1 .73 1.58 695
3 12.25 4.72 2.54   21 89   1.38    .47 .53 .8 3.85 .75 1.27 720
3 12.53   5.51 2.64   25 96   1.79   .6 .63 1.1   5 .82 1.69 515
3 13.49   3.59   2.19  19.5 88 1.62 .48 .58 .88 5.7 .81 1.82 580
3 12.84 2.96    2.61 24    101 2.32 .6 .53 .81 4.92 .89 2.15 590
3 12.93    2.81 2.7    21 96    1.54 .5 .53 .75 4.6 .77 2.31 600
3 13.36 2.56   2.35   20    89 1.4    .5 .37 .64 5.6 .7 2.47 780
3 13.52 3.17   2.72    23.5 97 1.55 .52 .5 .55 4.35 .89 2.06 520
3 13.62   4.95    2.35    20 92 2   .8 .47 1.02 4.4 .91 2.05 550
3 12.25 3.88 2.2 18.5 112    1.38 .78    .29 1.14 8.21 .65 2 855
3 13.16 3.57 2.15   21    102 1.5   .55   .43  1.3 4 .6 1.68 830
3 13.88 5.04   2.23    20 80   .98 .34 .4 .68 4.9   .58 1.33 415
3 12.87 4.61    2.48 21.5 86   1.7 .65 .47 .86 7.65 .54 1.86 625
3 13.32 3.24 2.38 21.5 92 1.93 .76 .45  1.25   8.42 .55 1.62 650
3 13.08 3.9 2.36 21.5 113 1.41 1.39 .34   1.14 9.40 .57 1.33 550
3 13.5 3.12 2.62 24 123 1.4    1.57 .22    1.25 8.60 .59 1.3 500
3 12.79 2.67 2.48 22 112    1.48 1.36 .24 1.26 10.8 .48 1.47 480
3 13.11 1.9 2.75 25.5 116  2.2 1.28    .26 1.56 7.1 .61 1.33 425
3 13.23 3.3 2.28  18.5 98    1.8 .83 .61 1.87 10.52 .56 1.51 675
3 12.58  1.29    2.1 20 103    1.48 .58 .53 1.4 7.6 .58 1.55 640
3 13.17 5.19    2.32    22 93  1.74 .63 .61 1.55 7.9 .6 1.48 725
3 13.84 4.12 2.38  19.5 89 1.8    .83 .48 1.56 9.01 .57 1.64 480
3 12.45 3.03 2.64    27 97   1.9 .58   .63 1.14 7.5 .67 1.73 880
3 14.34 1.68 2.7   25 98 2.8    1.31 .53     2.7 13 .57 1.96 660
3 13.48 1.67 2.64 22.5 89 2.6  1.1 .52 2.29   11.75 .57 1.78 620
3 12.36 3.83 2.38 21 88 2.3   .92 .5    1.04   7.65 .56 1.58 520
3 13.69 3.26 2.54 20 107 1.83  .56    .5 .8    5.88 .96 1.82 680
3 12.85 3.27 2.58 22 106 1.65    .6 .6 .96    5.58  .87 2.11 570
3 12.96 3.45 2.35 18.5 106 1.39   .7 .4 .94    5.28 .68 1.75 675
3 13.78 2.76 2.3 22 90 1.35 .68    .41 1.03    9.58  .7 1.68 615
3 13.73 4.36 2.26 22.5 88 1.28 .47 .52 1.15    6.62 .78 1.75 520
3 13.45 3.7 2.6 23 111 1.7 .92 .43    1.46    10.68 .85 1.56 695
3 12.82 3.37 2.3 19.5 88 1.48 .66    .4   .97 10.26 .72 1.75 685
3 13.58 2.58 2.69    24.5 105 1.55 .84 .39 1.54 8.66 .74 1.8 750
3 13.4  4.6    2.86    25 112 1.98 .96 .27 1.11 8.5 .67 1.92 630
3 12.2 3.03 2.32 19  96   1.25 .49   .4   .73 5.5   .66 1.83 510
3 12.77 2.39 2.28 19.5 86 1.39 .51 .48 .64 9.899999 .57 1.63 470
3 14.16  2.51    2.48    20 91 1.68 .7 .44 1.24 9.7 .62 1.71 660
3 13.71    5.65  2.45 20.5 95 1.68 .61 .52 1.06 7.7 .64 1.74 740
3 13.4 3.91 2.48    23    102 1.8   .75 .43 1.41 7.3 .7 1.56 750
3 13.27 4.28 2.26 20 120  1.59    .69 .43 1.35 10.2 .59 1.56 835
3 13.17 2.59 2.37    20    120 1.65 .68 .53 1.46 9.3 .6 1.62 840
3 14.13 4.1   2.74    24.5  96 2.05 .76 .56 1.35 9.2 .61 1.6 560