班里有 m 位学生,共计划组织 n 场考试。给你一个下标从 0 开始、大小为 m x n 的整数矩阵 score ,其中每一行对应一位学生,而 score[i][j] 表示第 i 位学生在第 j 场考试取得的分数。矩阵 score 包含的整数 互不相同 。
另给你一个整数 k 。请你按第 k 场考试分数从高到低完成对这些学生(矩阵中的行)的排序。
返回排序后的矩阵。
示例 1:
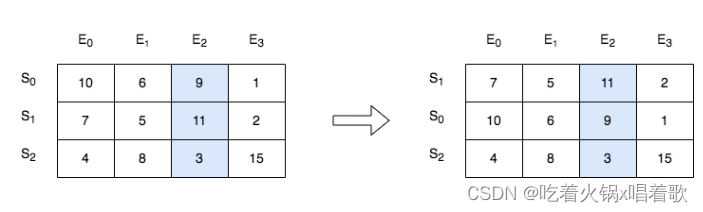
输入:score = [[10,6,9,1],[7,5,11,2],[4,8,3,15]], k = 2
输出:[[7,5,11,2],[10,6,9,1],[4,8,3,15]]
解释:在上图中,S 表示学生,E 表示考试。
- 下标为 1 的学生在第 2 场考试取得的分数为 11 ,这是考试的最高分,所以 TA 需要排在第一。
- 下标为 0 的学生在第 2 场考试取得的分数为 9 ,这是考试的第二高分,所以 TA 需要排在第二。
- 下标为 2 的学生在第 2 场考试取得的分数为 3 ,这是考试的最低分,所以 TA 需要排在第三。
m == score.length
n == score[i].length
1 <= m, n <= 250
1 <= score[i][j] <= 105
score 由 不同 的整数组成
0 <= k < n
解法一:直接排序:
class Solution {
public:vector<vector<int>> sortTheStudents(vector<vector<int>>& score, int k) {set<pair<int, int>, greater<pair<int, int>>> scoreAndId;int studentNum = score.size();for (int i = 0; i < studentNum; ++i) {scoreAndId.insert({score[i][k], i});}vector<vector<int>> res;for (pair<int, int> studentInfo : scoreAndId) {res.push_back(score[studentInfo.second]);}return res;}
};
如果有n个学生,此算法时间复杂度为O(nlgn),空间复杂度为O(n)。
解法二:原地排序:
class Solution {
public:vector<vector<int>> sortTheStudents(vector<vector<int>>& score, int k) {sort(score.begin(), score.end(), [k] (vector<int> &a, vector<int> &b) {return a[k] > b[k];});return score;}
};
如果有n个学生,此算法时间复杂度为O(nlgn),空间复杂度为O(1)。