**提醒！此题的解题思路及代码仅为我们团队的尝试，不确保正确，在数学建模过程中很多题目也没有确切答案 **

大体思路

由于是资源配置问题，所以最终肯定是建立一个优化模型。

解决过程

数据处理

首先，思考一下目标函数如何建立，最终要求的是2006年利润最大化并且对资源进行合理配置，由于题目中没有给出成本，所以需要列写的的也就是最大销售额的公式。由附件中给出数据进行分析后可知，最大销售额=2006年预测的单位书号销量x2006年给分社的书号数x课程均价。
所以第一步就是预测2006年的单位书号销量，用附件中给出的数据计算出2001-2005年的单位书号销量，再建立一个灰度模型预测2006年的单位书号销量。
目标函数大体就可以写出来了，接下来要处理的就是限制条件。由于附件中给出了很多数据，所以可用的很多，例如：书号一共500个，分配给各个分社的书号不得少于分社申请量的一半，找到强势产品，找到用户满意度高的产品，找到各个分社的最大工作能力。。。。。。

模型的建立

将处理好的数据建立一个优化模型，Lingo,Matlab，R都可以求解出各个分社的书号分配方案以及最大销售额。

注意事项

1、给出的数据存在有偏差的数据要及时筛选
2、不要被大量的数据搞乱，学会找到自己需要的数据

摘要

本文讨论出版社实现利润最大化并且对资源进行合理配置的问题。根据出版社的工作流程，我们将问题分为两个阶段。第一阶段是对附件中的数据进行处理，找出与销售额相关的因素并且进行计算；第二阶段是根据第一阶段处理好的数据，列写目标函数、2006年的最大销售额以及各个限制条件。
在建立模型确定第一阶段的数据处理时，由题目可知，由出版社一般以增加强势产品支持力度的原则进行优化资源配置，故本文侧重于找出强势产品即市场占有率高的科目。除此以外，本文也计算了每年的单位书号销量，利用 建立了灰预测 对2006年的单位书号销量进行了预测；通过附件计算出了各分社的实际销售完成比例的上下限和各分社的最大工作能力。
在第二阶段的书号分配过程中，我们利用第一阶段中求得的数据，在 中建立优化模型，列写出目标函数以及限制条件，找出实现2006年利润最大化的书号分配方案以及此方案下2006年的最大利润。
最后我们根据得出的结果，对出版社提出了相应的建议，给出了出版社在分配书号的过程中需要考虑的关键因素。

单位书号销量的灰预测模型的确立建立及求解

由于本题目标是2006年利润最大化并进行合理的资源配置，所以需要根据附件所给数据建立优化模型，找到目标函数以及限制条件。由附件三、四中所给数据，将各课程的实际销量除以各课程的分配书号数可以得出单位书号销量。由于2006获得的销售量为2006年的单位书号销量，分配的书号数以及课程均价的乘积，所以首先需要根据已有数据预测出2006年的单位书号销量。

根据附件三及附件四给出的各科目的实际销量以及各科目分配的书号数，将各科目的实际销量除以分配到的书号数得出单位书号销量，由于所知信息不完全且数量不大，故将2001-2005单位书号销量用 建立灰度模型预测2006年单位书号销量。

在对2001-2005年的实际销量以及书号数进行处理后得出2001-2005年的单位书号销量，在此数据基础上采用灰预测 对2006年的单位书号销量进行预测。本模型的最大优点在于需要的信息不多，只需要4个以上的数据就可以进行预测。首先计算出所有课程的单位书号销量如表1，由于数据过多，故本文只列写部分数据的单位书号销量，全部的数据见附录。

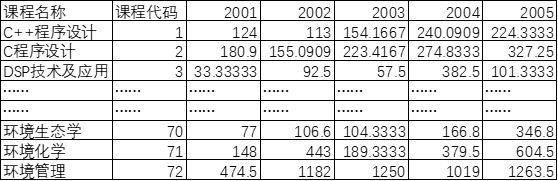
利用灰预测模型 以及上表得出的2001-2005年的单位书号销量，对所有课程2006年单位书号销量进行预测，数据如表2。

在将数据进行级别检验后，利用2001-2005年的单位书号销量进行数据预测，进行残差检验，求得的残差值均小于0.1，较精准地预测了2006年地单位书号销量。

各分社实际销售完成比例

由于各分社在申请书号时，出于本位利益存在夸大书号申请数，所以需根据各分社人力资源状况，找出各分社能完成的最多书号数。
由附件五可知各分社各部门的人数及该部门每人的工作能力，将各部门人数与该部门每个人的工作能力相乘求出各个部门的工作能力，将该分社的各部门进行比较，找出部门工作能力最低值，该数值就是此分社的最大工作能力即该分社能完成的最多书号数。

首先将各分社各部门的人数与工作能力相乘，计算出各部门的工作能力值，再通过对比找到工作能力最低的部门，该部门工作能力就是该分社的最大工作能力即该分社的最多完成书号数，如表4。

各分社市场占有率

由题意可知，本出版社采用增加强势产品的支持力度的原则优化资源配置。故针对附件二中所给数据，进行一定处理找出市场占有率较高的课程，将市场占有率高以及增长趋势明显的产品称为强势产品。由于附件二中数据庞大，首先对数据二中的数据进行处理。
将附件二中 出版社的的全部数据提取出来，即代号为 的数据进行提取，由于部分教材为高年级学生赠送、老师代复印的讲义、旧书等并非自主购买的课程数目，故在进行市场占有率的求解中将这些类别的数目剔除。
市场占有率的求解根据附件二中所得出的 出版社占有的某一课程除所有统计数据中该课程的总数，就可得出各分社的市场占有率。

根据附件二中给出的数据，找出 出版社的某一分社的个数除以附件二中所有统计数据中该课程的总数，找出该分社的市场占有率，如表5。

模型的建立与求解

对于总社而言加强优势产品支持力度来优化资源配置是必要的，由前面分析可知地理、地质类，环境类，能源、机械类为优势类，假如去年的书号分配方案为 ，则需分配给满足优势类的书籍书号大于去年分配给该书籍书号的个数，即需满足 。总上所述有：

通过上述数据，在 程序中建立优化模型，列写出目标函数2006年的销售函数以及通过由附件中得出的总书号数、各分社工作能力、各分社销售完成比例上下限以及各分社市场占有率等求得的限制条件，得到最大销售额，但由于数据量过大，将数据需要用到的数据放到Excel数据汇总表里，通过 函数读入数据，同时将结果输出到该表格，见表6。

在实际建模过程中，发现存在数据的下限约束条件高于该分社最大工作能力即通过计算得出的实际销售比例下限值大于该分社的最大工作能力，综合分析后，导致存在这样问题的原因是分社出于本位利益，过分夸大申请书号数，故这组数据决定采用分配给该分社的书号总数限制条件上限为最大工作能力，申请量的一半为下限。
通过 建立 线性规划模型后求解出全局最优解即最大销售额为23216420 元。

给出版社的建议

根据附件4各分社2001-2005年实际获得的书号，附件5各分社的人力资源细目以及本题得出的2006年各分社分配的书号，如表7，对各分社的人力资源进行横向和纵向的分析，为出版社提出一些有益的建议。

由上表可知，该出版社最多可完成的书号为812个，每年出版社只分配给各分社 500个书号，出版社仍有人力资源可以再完成312个书号，这部分未利用资源已经占据实际使用资源的一半以上，造成了人力资源的极大浪费。故出版社可以更多利用人力资源，适当增加书号数分配给各分社以提高销售量来提高出版社整体的利润或者进行适当裁员，在保证销售额的情况下减少人力的成本来提高出版社的利润。
由上表可知，2001-2006年该出版社的计算机类、数学类、英语类分到的书号较多，其他分社分到的书号较少。其中计算机类、数学类每年分到的书号虽然较多，但是这两个分社的人力资源完完全全能够完成分到的书号。但是作为同样分到书号较多的数学类，2001-2005年所分到的书号均大于历年平均最多能够完成的书号数，此分社的人力资源不足以完成2001-2005年分配到的书号数，这在本题中限制了2006年数学类分得的书号数目。而其他分到书号较少的分社的人力资源就显得偏多。所以应该进行出版社内部人力资源的调整，将其他人力资源富余的分社的部分策划、编辑、校对人员适当的调配到数学类分社去，同时也可以将工作能力比较出众的策划、编辑、校对人员分配到所得书号数目高或者销售量高的分社去，适当的分配出版社的人力资源，进一步提高出版社的市场占有率，所获利润和影响力。

代码

MATLAB灰预测代码

x=[474.5	1182	1250	1019	1263.5];%2001—2005年单位书号销量。
r=10000;%调节x使通过级比检验，作建模可行性分析，使适用灰色分析。
x=x+r;
n=5;%矩阵为,,,1*n,,,,。
k=0:n;%需要检验预测的年份设定值。
a=n+1;%需要预测的年份
y=cumsum(x,2);%累加。
q=[];%级比。
z=[];%均值。
u=[];%a,b。
f=[];%估计值。
for i=2:nq(:,i-1)=x(:,i-1)./x(:,i);%产生级比数。
end
if q>0.778800783&q<1.284025417%级比检验。for i=1:n-1z(1,i)=(y(1,i)+y(1,i+1))/2;%均值生成。endB=[-z(1,:)',ones(n-1,1)];Y=x(1,2:n)';u(1,1:2)=(B'*B)^(-1)*B'*Y;%解出预测常数a,b的值。f(1,:)=(x(1,1)-u(1,2)/u(1,1))*exp(-u(1,1)*k)+u(1,2)/u(1,1);%拟合方程。f=diff(f,1,2);%差分。f=[x(1,1),f];e=x(1,1:n)-f(1,1:n);%预测值与真实值的残差。average=mean(e);%残差均值。t=1-average;%模型预测精度。f=f-r;
end

LINGO优化模型代码

!需要数据汇总表的数据支持;
model:
sets:
subjects/1..72/:apply,x,predict,price,a,y;!a:1强势产品，0：不是强势产品，y:去年分配的书号。;
endsets
data:
apply=@ole(C:\Users\asus\Desktop\数据汇总表.xlsx,B2:B73);!注意路径;
!从Excel表格（B2:B73）数据区里读出数据;
predict=@ole(C:\Users\asus\Desktop\数据汇总表.xlsx,C2:C73);
price=@ole(C:\Users\asus\Desktop\数据汇总表.xlsx,D2：D73);
a=@ole(C:\Users\asus\Desktop\数据汇总表.xlsx,F2:F73);
y=@ole(C:\Users\asus\Desktop\数据汇总表.xlsx,E2:E73);
@ole(C:\Users\asus\Desktop\数据汇总表.xlsx,G2:G73)=x;
!将分配结果输入到Excel表格（G2:G73）数据区;
enddata
[obj]max=@sum(subjects:x*predict*price);!目标函数:销售额最大原则;
@sum(subjects:x)=500;!总数约束条件;
@for(subjects:x>=apply/2);!申请量半数约束条件;
@for(subjects:x<=apply);!申请量约束条件;
@for(subjects|a#eq#1:x>=y);!支持优势产品原则;
@sum(subjects(i)|i#ge#1#and#i#le#10:x(i))<=83.46;!申请夸大不精确度的上下限约束，分社最大工作能力约束。;
@sum(subjects(i)|i#ge#11#and#i#le#20:x(i))<=49.12;
@sum(subjects(i)|i#ge#21#and#i#le#30:x(i))<=120;
@sum(subjects(i)|i#ge#31#and#i#le#40:x(i))<=90.2998;
@sum(subjects(i)|i#ge#41#and#i#le#48:x(i))<=52.11;
@sum(subjects(i)|i#ge#49#and#i#le#54:x(i))<=58.39;
@sum(subjects(i)|i#ge#55#and#i#le#60:x(i))<=28.84;
@sum(subjects(i)|i#ge#61#and#i#le#66:x(i))<=30.54;
@sum(subjects(i)|i#ge#67#and#i#le#72:x(i))<=27.70;
@sum(subjects(i)|i#ge#1#and#i#le#10:x(i))>=73.47;
@sum(subjects(i)|i#ge#11#and#i#le#20:x(i))>=42.60;
@sum(subjects(i)|i#ge#21#and#i#le#30:x(i))>=111;
@sum(subjects(i)|i#ge#31#and#i#le#40:x(i))>=76.16;
@sum(subjects(i)|i#ge#41#and#i#le#48:x(i))>=46.33;
@sum(subjects(i)|i#ge#49#and#i#le#54:x(i))>=51.55;
@sum(subjects(i)|i#ge#55#and#i#le#60:x(i))>=26.30;
@sum(subjects(i)|i#ge#61#and#i#le#66:x(i))>=24.47;
@sum(subjects(i)|i#ge#67#and#i#le#72:x(i))>=24.44;
@for(subjects:@gin(x));!自然数约束;
End